Overview
Session Summary
This session is the first of three in which you will focus on addition and subtraction. During these sessions you will look at the meaning of the operation, explore contexts and representations, and consider several computational strategies for solving problems. You will watch short segments of videotapes that provide examples of students working on whole number computation and demonstrate how students build their understanding of the operations. This session will focus on Addition.
Session Focus
In this session you will:
- Consider what students need to know in order to be able to add
- Consider contexts and representations that support understanding the meaning of addition
- Examine strategies that students use to solve addition problems
- Examine the foundations for computational fluency when using the operation of addition
Materials
Please have the following available for this session: 48 Unifix or linking cubes in one color and 25 in another color.
Note: The Common Core Standards states that the U.S. Standard Algorithm for addition and subtraction are to be studied in grade four. Think about the foundational concepts that are practiced in the grades before so fourth grade students can, not only perform the steps of the U.S. Standard Algorithm, but also understand the meaning behind the steps in these algorithms.
Getting Started: Building a Structure of Ten
Ten-Frame Quick Images
Ten-Frames help students organize sets of objects in order to make them easier to count and combine. Students describe the spatial representations, and develop visual images for various quantities. Using Ten-Frames helps students establish 10 as a unit, and pushes them to use it as a benchmark - seeing numbers in terms of ten. Ten-Frames are a great representation to help students to develop fluency with number combinations to 10 + 10.
Read
Second Grade Ten-Frame Classroom Routine
Notebook
Respond to the following questions in your notebook.
- How do Ten-Frames help students become more efficient in their counting?
- How do Ten-Frames help students become more efficient in at decomposing numbers to find a sum?
- How do Tens-Frames support students’ computation skills and building a system of ten?
Early Approaches to Solving Story Problems
Mentally solve the following problem.
Kim has 6 cars.
Her friend gave her 7 more cars.
How many cars does Kim have now?
You may have found the sum (13) using a math fact. The following are examples of ways.
These examples remind us that even with a problem as simple as 6 + 7 there is more than one way to solve the problem and arrive at a correct solution. Young students commonly use one of three approaches to solving an addition story problem: counting all, counting on or using numerical reasoning. It’s important to observe and listen to students at work to understand their approach.
The ability to work with chunks greater than one and numerical reasoning develops gradually over the early elementary years. As students build their understanding of number combinations, place value and number relationships, as well as their ability to visualize the structure of the problem as a whole, they will begin to develop more efficient and flexible strategies.
Sharing Strategies (Class Discussion)
Kim has 6 cars.
Her friend gave her 7 more cars.
How many cars does Kim have now?
Watch the class discussion as they share their strategies and their teacher notates three approaches to solving the same problem: Counting All, Counting On and Numerical Reasoning. Pay attention to how she guides the discussion about strategies.
Read
Discussing Addition Strategies from Number Games and Crayon Puzzles (Grade 1)
Discussing Addition Strategies, from Landmarks and Large Numbers (Grade 4)
Notebook
Record your thoughts in your notebook.
In what ways does discussing and sharing strategies help students?
Readings
Discussing Addition Strategies from Number Games and Crayon Puzzles (Grade 1)
Students’ Addition Strategies, from Partners, Teams, and Paper (Grade 2)
Adding 2-Digit Numbers, from How Many Tens? How Many Ones? (Grade 2)
Addition Strategies, from How Many Hundreds? How Many Miles? (Grade 3)
The Case of Ezra Who “Just Knows” the Answer from Implementation Guide (Grade 3)
Learning and Assessing Addition Combinations from Trading Stickers, Combining Coins, (Grade 3)
Discussing Addition Strategies, from Landmarks and Large Numbers (Grade 4)
The readings above are all published in Russell, S.J.; Economopoulos, K.; Wittenberg, L.; et al. Investigations in Number, Data, and Space®, Second Edition. Glenview: Pearson, 2012.
Activity 1: Solving Addition Problems Using Mental Math
In this activity, you will:
- solve a problem mentally
- explore visual representations of strategies in order to focus on the action of the first steps of various strategies.
Addition Problem
You will begin by mentally solving an addition problem. Often our mental strategies—like the ones we might use while at the grocery store - are the ones that best show our flexibility and use of number relationships.
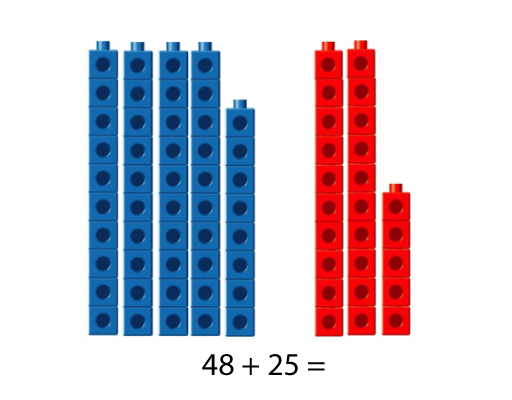
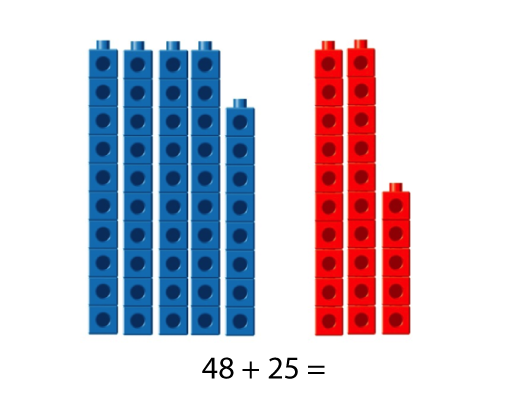
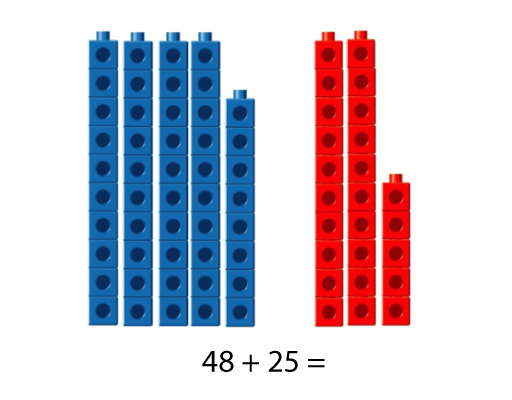
48 + 25
- Mentally solve the problem.
- Record your thinking as you mentally solve 48 + 25.
Below are three different strategies. Look for similarities among the strategies, particularly those that start with the same first step, but have subtle differences in the final steps. There are three or four basic strategies, not dozens.
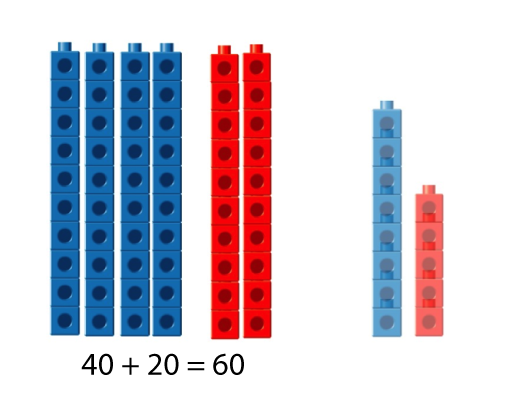
Adding by Place
- 48 + 25
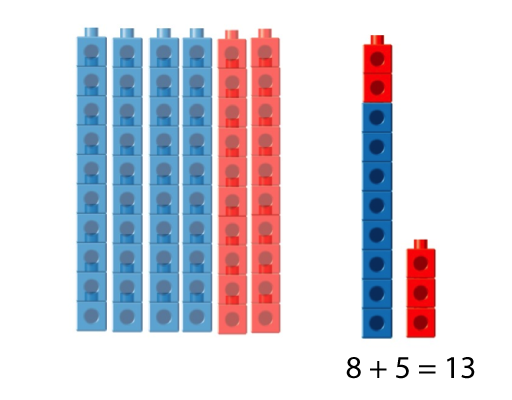
- 40 + 20 = 60
- 8 + 5 = 13
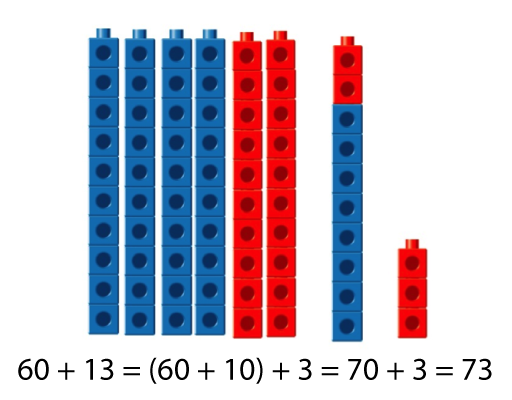
- 60 + 13 = 73
- * Also described as: adding tens and ones
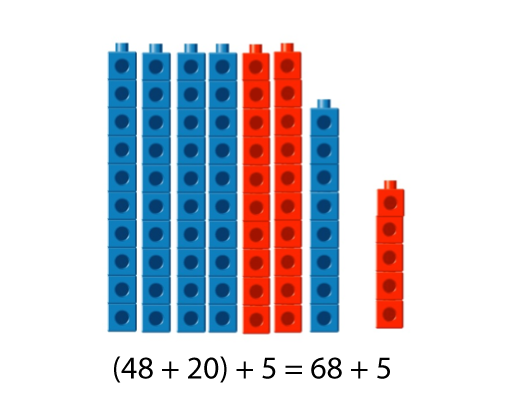
Keeping one number whole and the other in parts
- 48 + 25
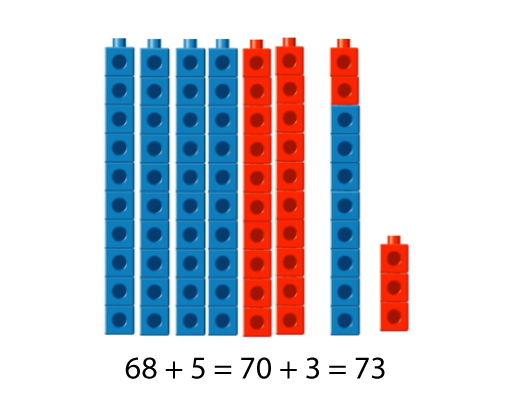
- 48 + 20 = 68
- 68 + 5 = 73
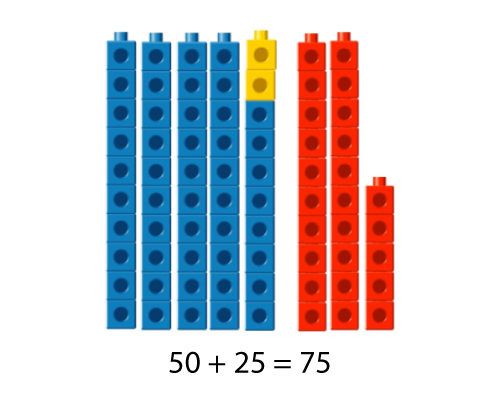
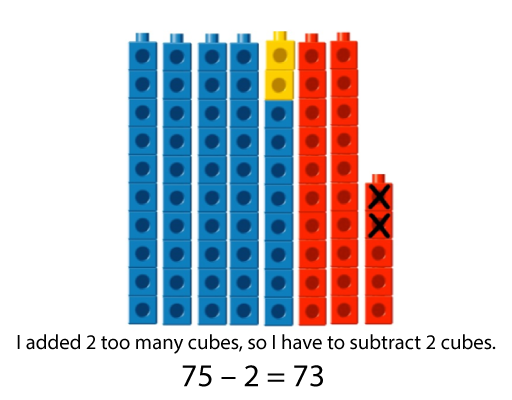
Adjusting and compensating
- 48 + 25
- 50 + 25 = 75
- 75 – 2 = 73
- * Also described as: changing the numbers
Using Models
Choose a strategy (yours or one of the three that are illustrated above). Using Multilink cubes or Unifix cubes, take 48 cubes in one color and 25 cubes in another color. Act out the steps of the strategy using the cubes.
Focus on just the first step of the strategy. Use a blank paper as a mat. Model the first step of your strategy on the mat. (Any cubes that weren’t part of the first step can be left off to the side.)
Review the different strategies in the following slideshow.
Note: Students sometimes use “run-on-equations.” When you record student strategies, make sure not to use “run-on-equations.”
Students often record “run-on-equations” such as:
40 + 20 = 60 + 8 = 68 + 5 =73
This is incorrect.
While 40 + 20 = 60, 40 + 20 ≠ 60 + 8 and 60 + 8 ≠ 68 + 5.
The correct way to record this thinking is using three separate equations:
40 + 20 = 60
60 + 8 = 68
68 + 5 = 73
Read
Read the following Teachers Notes – they further describe addition strategies across the grade levels.
Activity 2: Students Sharing Their Strategies
In this activity, you will view video clips of students demonstrating different strategies to solve 48 + 25.
Stacie and Harrison
Zoe, Elthea, James
Use each of the students' strategies to solve 54 + 37.
Chris and Isaiah
Use Chris and Isaiah's strategies to solve 250 + 687.
Final Thoughts…
As students share their strategies, they:
- compare their approaches and make generalizations about how the operations work,
- discuss how to adjust strategies to make them more efficient problems
- make connections between different operations (e.g., addition and subtraction)
- apply their strategies to more complex problems.. These conversations encourage students to think flexibly about solving problems in different ways.
Activity 3: Starter Problems
In this activity, you will work on Addition Starter Problems. You will solve the same problem with different “starts,” or first steps.
One goal for students as they develop computational fluency with the operation of addition is to be flexible. We want students to have several strategies to choose from depending on the number relationships presented in a particular problem. Starter Problems encourage students to expand their repertoire of strategies. As you solve these problems, think about how starter problems help to develop flexibility.
Sample Starter Problem
288 + 456
- Estimate the sum.
About how many hundreds will the answer have?
What do you have to pay attention to in order to know how many hundreds?
Solve the problem 288 + 456 using three different “starts.”
Students might say things like:
- The answer will be more than 700.
- There are 200 and 400 and then one more hundred because 88 plus 56 is more than 100.
Notebook
Record how you solved 288 + 456 using each of the following starter problems:
- Start with 288 + 400 = ____ to solve 288 + 456. Complete the problem.
- Start with 200 + 400 = ____ to solve 288 + 456. Complete the problem.
- Start with 300 + 450 = ____ to solve 288 + 456. Complete the problem.
Think about…
- Which “start withs” made it easiest for you to solve 288 + 456? Explain why.
- Which of the “start withs” challenged you? Explain why.
- How might starter problems help students think more flexibly about addition problems?
Record your response in your notebook.
Optional: If you would like to try more starter problems, here are a few from grade 4.
We want students to be accurate, efficient, and flexible. As you saw in the video and know from your own experiences, efficiency varies from one individual to another.
Think about how the work you did in this session links to the work your students do with the operation of addition.
Discussion
How do contexts and representations help students develop understanding of the addition operation? Cite examples from the session activities, readings or video.
How do Starter Problems help students identify, describe and compare addition strategies?
Remember to post early and return to the discussion forum throughout the week to read and respond to others’ posts.
Common Core Alignment
The content in this session is aligned to the following Common Core State Standards and Math Practices:
MATH PRACTICES
MP1: Make sense of problems and persevere in solving them.
MP2: Reason abstractly and quantitatively
MP4: Model with mathematics
MP5: Use appropriate tools strategically
MP6: Attend to precision
You may also wish to review the full set of Common Core State Standards in Math and/or videos of the Math Practices enacted in Investigations.
This chart was created by Bill McCallum in an attempt to provide some higher order structure to the practice standards, just as the clusters and domains provide higher order structure to the content standards.
MATH STANDARDS
Know number names and the count sequence.
- CCSS.Math.Content.K.CC.A.2 Count forward beginning from a given number within the known sequence (instead of having to begin at 1).
- CCSS.Math.Content.K.CC.A.3 Write numbers from 0 to 20. Represent a number of objects with a written numeral 0-20 (with 0 representing a count of no objects)
Count to tell the number of objects.
- CCSS.Math.Content.K.CC.B.4 Understand the relationship between numbers and quantities; connect counting to cardinality.
- CCSS.Math.Content.K.CC.B.4a When counting objects, say the number names in the standard order, pairing each object with one and only one number name and each number name with one and only one object.
- CCSS.Math.Content.K.CC.B.4b Understand that the last number name said tells the number of objects counted. The number of objects is the same regardless of their arrangement or the order in which they were counted.
- CCSS.Math.Content.K.CC.B.4c Understand that each successive number name refers to a quantity that is one larger.
- CCSS.Math.Content.K.CC.B.5 Count to answer “how many?” questions about as many as 20 things arranged in a line, a rectangular array, or a circle, or as many as 10 things in a scattered configuration; given a number from 1–20, count out that many objects.
Compare numbers.
- CCSS.Math.Content.K.CC.C.6 Identify whether the number of objects in one group is greater than, less than, or equal to the number of objects in another group, e.g., by using matching and counting strategies.1
- CCSS.Math.Content.K.CC.C.7 Compare two numbers between 1 and 10 presented as written numerals.
Operations and Algebraic Thinking
- Understand addition as putting together and adding to, and understand subtractions as taking apart and taking from (K)
- Represent and solve problems involving addition and subtraction (1 and 2)
- Understand and apply properties of operations and the relationship between addition and subtraction (1)
- Add and subtract within 20 (1 and 2)
- Work with addition and subtraction equations (1)
- Work with equal groups of objects to gain foundations for multiplication (2)
- Use the four operations with whole numbers to solve problems [in this case, addition and subtraction (4)]
K.OA.1-5
1.OA.1-8
2.OA.1, 2
3.OA.8
4.OA.3
Number and Operations in Base Ten
- Work with numbers 11-19 to gain foundations for place value (K)
- Extend the counting sequence (1)
- Understand place value (1 and 2)
- Use place value understanding and properties of operations to add and subtract (1 and 2)
- Use place value understanding and properties of operations to perform multi-digit arithmetic (3, 4 and 5)
- Generalize place value understanding for multi-digit whole numbers (4)
- Understand the place value system (5)
K.NBT.1
1.NBT.2abc
1.NBT.4-6
2.NBT.1ab, 2.NBT.5-9
2.MD.5
3.NBT.1
3.NBT.2
4.NBT.1-4
5.NBT.1
Key Learning
- To solve problems efficiently and flexibly students need to develop the building blocks of computation.
- As students work on story problems, the focus is on students making sense of the action in the problems and on them developing strategies that make sense to them to solve the problems.
- Young students commonly use one of three approaches to solving a story problem: counting all, counting on or back, or numerical reasoning (using numbers they know).
- Working on number composition encourages flexibility with numbers, helps students learn addition facts and exposes them to ideas about place value.
- Students learn combinations (facts) best by using strategies and not just simply rote memorization.
- As students estimate sums to problems they develop strategies for mental computation and can use their estimates to judge the reasonableness of exact answer solutions.
- Describing, analyzing, and comparing strategies is an important part of the work of students in grades three, four, and five in order to develop strategies they can apply efficiently and flexibly to solve more complex problems.
- Upper elementary fluently add using strategies and algorithms based on place value and properties of operations.
Notebook
Fill out the Session 1 Notebook Page to reflect on your own learning and record ideas that you want to remember and/or try with students.
Select the links to go to the Notebook.