Overview
Session Summary
In this session, you will examine how children make sense of the operation of subtraction and develop strategies for solving subtraction problems. You will explore different contexts for subtraction problems; engage in mental math and consider various strategies for solving subtraction problems; learn about recording subtraction strategies on unmarked number lines; view video clips of students sharing their subtraction strategies and look at written student work.
Session Focus
In this session you will:
- Consider what students need to know in order to be able to subtract
- Consider contexts and representations that support understanding the meaning of subtraction
- Examine strategies that students use to solve subtraction problems
- Examine the foundations for computational fluency when using the operation of subtraction
Materials
Please have the following available for this session:
50 multilink or Unifix cubes (two colors)
Note:
In grade four in Investigations, students formally study the U.S. Standard Algorithm for subtraction and compare it to the strategies they have been using. Teaching Note sidebars appear starting in grade two with suggestions for addressing the U.S. Standard Algorithm when students bring it up.
Getting Started: Early Subtraction Strategies and Situations
Students solve addition and subtraction story problems beginning in Kindergarten and continue this work throughout the grades. As students work on story problems, the focus is on students making sense of the action of different types of problems and developing strategies to solve them. You will begin by looking at how young students interpret and solve subtraction story problems.
Types of Subtraction Problems
Students are first introduced to story problems in Kindergarten and first grade. They mainly work on addition problems and on subtraction problems that are called “removal” problems. These problems involve removing, separating, taking away, losing, eating, etc. Later in first grade and throughout the rest of the Investigations curriculum, students will encounter two other types of subtraction situations – Comparing Two Amounts and Finding a Missing Part.
Take a look at the three problems in the VoiceThread below.
Having trouble viewing this voicethread? Click here.
Story Problem Routine
When students are introduced to a problem they are asked to visualize what happened in the story, retell the story and think about the action in the story. The Story Problem Routine is introduced to help students visualize and model the action in the story problems.
The Story Problem Routine sequence is as follows:
- Tell students a number story. Encourage them to visualize the action in the story.
- Ask several students to retell the story after they have heard it (Or several students can each tell one part of the story. Occasionally, you might have each student retell the story to a partner.)
- After retelling each story, ask whether the end result in each case will be more or less than the amount you started with.
- Ask students to share strategies for solving the problem, including modeling the problem with cubes or counters.
- Model methods for recording on chart paper or on the board.
Early Subtraction Strategies
Think about strategies a first grade student might use to solve this problem.
Max had 12 toy cars. His friend Rosa came over to play with him.
Max gave 4 of the cars to Rosa.
How many cars did Max have left?
Click on the headings below to see examples of strategies first grade students might use to solve the problem.
Students may use a variety of manipulatives to represent their strategy: pencils, cubes, fingers, etc.
Student use what they know about number relationships to take numbers apart and manipulate them. They also use their knowledge of the addition and subtraction operations.
Counting All
Students who “count all” count three times to solve a subtraction problem. They count the total, count the amount they are subtracting, and then count to see what is left to find the answer.
Counting On or Counting Back
When students count on or count back they start with a quantity and count on from that number. They do not need to construct the number from beginning by 1’s.


- Counting forward or backward (using cubes, on a number line, mentally or on their fingers)
Numerical Reasoning
- Uses knowledge of addition
- “I know 12 - 2 = 10. I need to take two more away 10 - 2 = 8, so 12 - 4 = 8”
Observing Students
The first grade class in the following video shares strategies to solve:
Libby had 10 goldfish crackers for snack.
She shared her snack with Jonah and gave him four.
The teacher asks the students to retell the story, they discuss the action in the story and then several students share their strategies.
Watch how the teacher first sets up the story problem expectations.
She then facilitates a discussion using the story problem routine.
Notebook
Think of several moves the teacher made to help students work independently on story problems. Record your thoughts in your notebook.
Readings
How Are These Stories Different from How Many Do You Have (Grade K)
Three Approaches to Story Problems from Number Games and Crayon Puzzles
A Subtraction Story Aloud from Number Games and Crayon Puzzles (Grade 1)
A Subtraction Story from Counting, Coins and Combinations (Grade 2)
Notating Subtraction Strategies from Partner, Teams, and Paper Clips (Grade 2)
Order and Subtraction from Stickers, Number Strings, and Story Problems (Grade 2)
Subtraction Strategies from Landmarks and Large Numbers (Grade 4)
Types of Subtraction Situations from Collections and Travels (Grade 3)
Representing Subtraction on the Number Line from Landmarks and Large Numbers (Grade 4)
The readings above are all published in Russell, S.J.; Economopoulos, K.; Wittenberg, L.; et al. Investigations in Number, Data, and Space®, Second Edition. Glenview: Pearson, 2012.
Activity 1: Mental Math
In this activity you will look at strategies for solving subtraction problems with two-digit numbers. You will solve two problems mentally and use the number line as a tool for recording strategies.
35 – 16
- Mentally solve the problem.
- Keep track of your steps in your notebook.
- Record your thinking as you mentally solve 35 - 16.
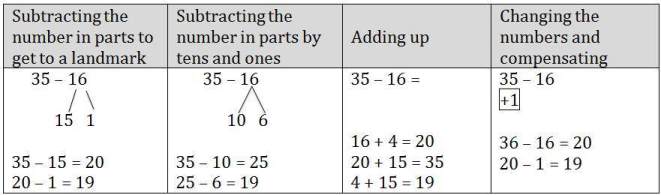
Subtraction Strategies
Click on the show link to examine several subtraction strategies.
Use linking cubes or this online virtual manipulative to illustrate the action of each of the four strategies. If you use the online manipulative, here are some instructions:
- to pick a cube, click on the Stamp icon at the top and then click on the color cube you want
- to link cubes, click on the hand and drag it to the cube you want to link with another cube
- to unlink cubes, click on the icons showing cubes separating, and then click on the ones you want to separate
- to 'delete' a cube, use the eraser, at the bottom, next to the broom
- to clear everything, click on the broom
Think about the first step and what follows.
92 - 58
- Mentally solve the problem.
- Use a strategy shown in the 35 - 16 problem.
- Keep track your steps in your notebook.
Using an Unmarked Number Line as a Tool to Show Thinking.
Read
The Teacher Note, Subtraction Strategies describes students’ most common subtraction strategies based on the first steps taken to solve a subtraction problem. Review the strategies in this Teacher Note.
Keep in mind, the unmarked number line is not a strategy, but rather a tool for representing strategies.
Subtraction Strategies
In the following examples, notice where the answer to the problem is on each of the number lines. Sometimes it is the total of the jumps you have made, while other times it is the place where you land on your final jump.
73 – 47
- Use one or more of the subtraction strategies demonstrated in the Screencast above to solve 73- 47.
- Show your thinking on an open number line.
- Record an equation for each step.
Think about how using an open number line supports your understanding of subtraction.
Activity 2: Exploring Subtraction
In this activity you will watch three different students solving a subtraction problem. Pay close attention to the students' approaches to solving the problems. You will apply those approaches to a new problem involving slightly larger numbers.
Lisa
You will watch Lisa, a 2nd grade student, solving 40 – 26.
Notebook
Reflect on the following questions in your notebook.
- What was Lisa’s first step?
- What were the rest of the steps in her strategy?
- What does Lisa understand about subtraction?
Use an open number line to record Lisa’s approach to solving 40 – 26.
About Lisa’s strategy.
- Lisa is subtracting in parts.
- Lisa saw 26 as 20 + 6. Her first step was to subtract 6 and then she subtracted 20.
- Lisa’s strategy works because she has taken the number apart and subtracted the parts one step at a time.
Naillil
Next you will watch Naillil (pronounced Ny-Jill) solve 40 - 26.
- Use an open number line to show Naillil’s approach to solving 40 – 26.
- Write an equation that shows Naillil’s strategy.
Notebook
- What does Naillil understand about subtraction?
- Write an equation that shows Naillil’s strategy.
- How do the two number line representations of Naillil’s and Lisa’s strategies compare?
Record your responses in your notebook
Adding up is a very common student strategy. It involves an understanding of the relationship between addition and subtraction and the use of landmark numbers. Adults often use this strategy to figure out the amount of change they are due. For example, if your bill is $26.00 and you give the cashier $40.00, (s)he might use Naillil’s strategy to count up from $26.00 to $40.00.
Subtracting Larger Numbers
1,405 – 619
- Solve 1,405 – 619 using a subtraction strategy described in the Teacher Note: Subtraction Strategies.
(subtracting one number in parts, adding up, changing and compensating, changing to an equivalent problem)
This video is of a 5th grade discussion of one student’s strategy. As you watch the students and teacher, think about how interpreting another person’s strategy helps students think flexibly.
Notebook
How did the teacher use a student’s strategy of breaking 619 apart to highlight the use of landmark numbers to make the problem easier to solve? Respond in your notebook.
Read
In addition to using a number line as a tool, students keep track of their strategies and notate them in a variety of ways. The following Teacher Notes illustrate how students might do this:
Notating Subtraction Strategies, from Partner, Teams, and Paper Clips (Grade 2)
Subtraction Strategies, from Landmarks and Large Numbers (Grade 4)
Activity 3: Looking at Student Work
So far in this session you’ve been working with subtraction problems that involve two-digit numbers. Next you are going to look at some student work of students from grades four and five working with larger numbers.
Solve the following problem:
1,403 - 877 =
- Estimate the answer.
- Solve the problem two different ways.
- Use at least one of the strategies from Activity 2.
Looking at Student Work
In this activity you will:
- Look at the sets of student work, one set at a time. Each set contains four related samples of student work. They are grouped together to explore particular focus questions.
- Answer the focus questions posed in your Notebook.
Set 1: 1,403 – 877
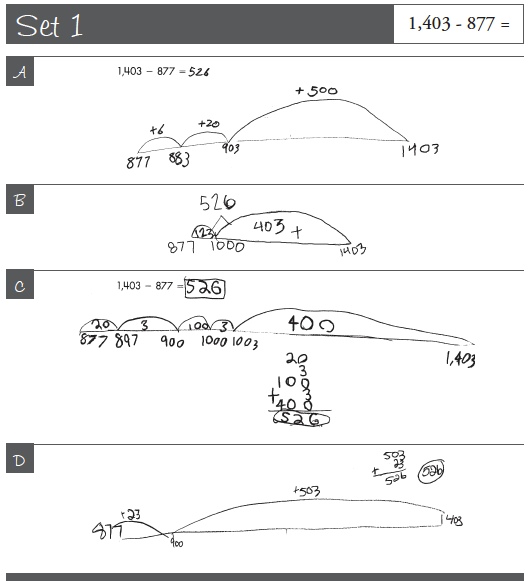
Focus question: Each of these students has used an adding up strategy. Notice how many jumps each student takes and what landmarks they choose to stop at.
What number relationships are they paying attention to as they determine their jumps? Record your responses in your Notebook.
Set 2: 621 - 319
- Read the story problem below.
- Estimate the answer.
- Solve the following problem in two different ways.
- Use at least one of the strategies from Activity 2.
Frannie’s family drives to a family reunion each summer. The reunion is always in a place that is 621 miles from Fannie’s house. On the first day, Frannie’s family drives 319 miles. How many more miles do they have to go until they get to the family reunion?
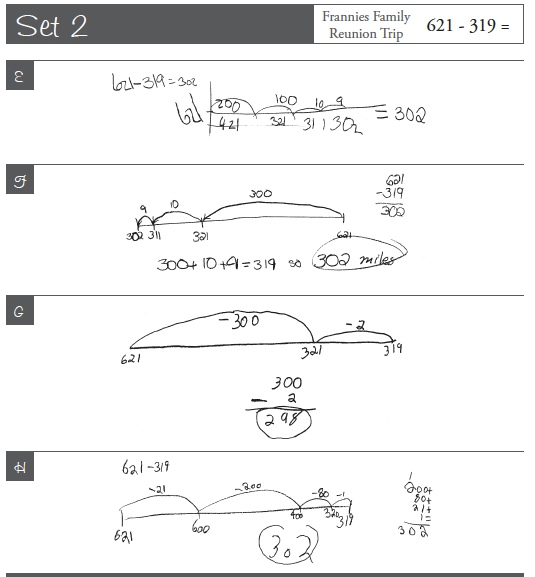
Focus question: Notice the various uses of the number line in these strategies.
Where in the representation do you find the answer to the problem?
Which students are subtracting back and which students are subtracting in parts? Record your responses in your Notebook.
Set 3: 621 - 319

Focus: Compare how the students break up 319 and how they use the parts 300, 10, and 9 in their strategies. Record your response in your Notebook.
Set 4: 621 - 319

Focus: Show each student’s strategy on a number line or use another representation; if there is an error, explain why. Record your response in your Notebook.
Discussion
How do contexts and representations develop students’ understanding and flexibility for solving subtraction problems K-5?
Remember to post early and return to the discussion forum throughout the week to read and respond to others’ posts.
Common Core Alignment
The content in this session is aligned to the following Common Core State Standards and Math Practices:
MATH PRACTICES
Subtraction strategies
MP1: Make sense of problems and persevere in solving them.
MP2: Reason abstractly and quantitatively
MP5: Use appropriate tools strategically
MP6: Attend to precision
Understanding structure of 100 and 1000:
MP4: Model with mathematics
MP5: Use appropriate tools strategically
MP6: Attend to precision
You may also wish to review the full set of Common Core State Standards in Math and/or videos of the Math Practices enacted in Investigations.
This chart was created by Bill McCallum in an attempt to provide some higher order structure to the practice standards, just as the clusters and domains provide higher order structure to the content standards.
MATH STANDARDS
Counting and Cardinality
Know number names and the count sequence.
- CCSS.Math.Content.K.CC.A.2 Count forward beginning from a given number within the known sequence (instead of having to begin at 1).
- CCSS.Math.Content.K.CC.A.3 Write numbers from 0 to 20. Represent a number of objects with a written numeral 0-20 (with 0 representing a count of no objects)
Count to tell the number of objects.
- CCSS.Math.Content.K.CC.B.4 Understand the relationship between numbers and quantities; connect counting to cardinality.
- CCSS.Math.Content.K.CC.B.4a When counting objects, say the number names in the standard order, pairing each object with one and only one number name and each number name with one and only one object.
- CCSS.Math.Content.K.CC.B.4b Understand that the last number name said tells the number of objects counted. The number of objects is the same regardless of their arrangement or the order in which they were counted.
- CCSS.Math.Content.K.CC.B.4c Understand that each successive number name refers to a quantity that is one larger.
- CCSS.Math.Content.K.CC.B.5 Count to answer “how many?” questions about as many as 20 things arranged in a line, a rectangular array, or a circle, or as many as 10 things in a scattered configuration; given a number from 1–20, count out that many objects.
Compare numbers.
- CCSS.Math.Content.K.CC.C.6 Identify whether the number of objects in one group is greater than, less than, or equal to the number of objects in another group, e.g., by using matching and counting strategies.1
- CCSS.Math.Content.K.CC.C.7 Compare two numbers between 1 and 10 presented as written numerals.
Operations and Algebraic Thinking
- Understand addition as putting together and adding to, and understand subtractions as taking apart and taking from (K)
- Represent and solve problems involving addition and subtraction (1 and 2)
- Understand and apply properties of operations and the relationship between addition and subtraction (1)
- Add and subtract within 20 (1 and 2)
- Work with addition and subtraction equations (1)
- Work with equal groups of objects to gain foundations for multiplication (2)
- Use the four operations with whole numbers to solve problems [in this case, addition and subtraction (4)]
K.OA.1-5
1.OA.1-8
2.OA.1, 2
3.OA.8
4.OA.3
Number and Operations in Base Ten
- Work with numbers 11-19 to gain foundations for place value (K)
- Extend the counting sequence (1)
- Understand place value (1 and 2)
- Use place value understanding and properties of operations to add and subtract (1 and 2)
- Use place value understanding and properties of operations to perform multi-digit arithmetic (3, 4 and 5)
- Generalize place value understanding for multi-digit whole numbers (4)
- Understand the place value system (5)
K.NBT.1
1.NBT.2abc
1.NBT.4-6
2.NBT.1ab, 2.NBT.5-9
2.MD.5
3.NBT.1
3.NBT.2
4.NBT.1-4
5.NBT.1
Key Learning
- Understanding the action and meaning of subtraction (removal, finding the difference between two numbers, comparing two numbers)
- As students estimate solutions to subtraction problems they develop strategies for mental computation and can use their estimates to judge the reasonableness of exact answer solutions
- When you subtract a small number from a large number the answer is smaller (true for positive whole numbers)
- Using a context for a problem often makes it much easier to solve
- Using a representation such as a number line helps you keep track of the steps in a subtraction problem
- Describing, analyzing, and comparing strategies is an important part of the work students do to develop strategies they can apply efficiently and flexibly to solve more complex problems
- Students add and subtract using strategies and algorithms based on place value, properties of operations and / or the relationship between addition and subtraction
Notebook
Fill out the Session 2 Notebook Page to reflect on your own learning and record ideas that you want to remember and/or try with students.
Select the following links to go to the Notebook.