- Overview
- Readings & CCSS
- Activity 1
- Activity 2
- Activity 3
- Activity 4
- Discussion
- Key Learning
- Notebook
Overview
Session Summary
In this session you will focus on decomposing numbers. You will consider the significance of decomposing numbers in the development of computational fluency and examine how students strategize in breaking numbers apart in order to solve problems flexibly. Jot down ideas or questions related to your own students as you move through this session.
Computational fluency is at the core of the work in the elementary grades. Students develop meaning of the operations, structure of the base-ten number system, and a repertoire of number combinations. Computational fluency has different meaning at each grade.
Watch and listen to Investigations author Susan Jo Russell as she describes the three facets of computational fluency.
Session Focus
In this session you will:
- Consider the significance of decomposing in the development of computational fluency K-5.
- Examine places in Investigations where breaking numbers apart contributes to students’ flexibility and efficiency in solving problems.
Materials
Please have the following available for this session:
- Digit Cards
- Calculator
Practice and Review
Listen to Investigations authors talking about practice and review opportunities in this clip.
Notebook
What practice are you using with your students to support them as they develop computational fluency? Record your reflections in your notebook.
Getting Started: Comparing Numbers
In Kindergarten through second grade students begin to compare numbers and learn about which is smaller, greater, the same as, and the difference between. The following Compare games from K-2 give students opportunities to practice comparing numbers.
Dot Compare
Each player turns a card over and compares the number of dots. They count the dots, say the number and then determine who has more. The player with the largest number wins.


Compare
Like Dot Compare, each player turns a card over and compares the number. They say the number and the compare the numbers. The player with the largest number wins.

Double Compare
Each player turns two cards over. They find the sum and then compare their sums. The player with the largest sum wins.


- Student counts from 6: "6, 7, 8"
- "I have 8."
- "I have more."

- "I used the pictures."
- "I know 3 and 3 more is 6.
- "6 and 1 more is 7."
- "You have more."
Read
Double Compare- Strategies for Combining and Comparing
Compare Game Materials
Readings
- Double Compare - Strategies for Combining and Comparing from How Many of Each? (Grade 1)
- The Relationship Between Addition and Subtraction, from Number Games and Crayon Problems (Grade 1)
- Place Value in Grade 2 from How Many Tens, How Many Ones (Grade 2)
- Place Value from Trading Stickers, Combining Coins (Grade 3 )
- Mathematical Representations for Addition and Subtraction from Trading Stickers, Combining Coins (Gr. 3)
- Breaking Numbers Apart for Addition from Collections and Travel Stories (Grade 3)
- I Know It’s Either 2 More or 2 Less from How Many Hundreds? How Many Miles? (Grade 3)
- Place Value from Landmarks and Large Numbers (Grade 4)
- Place Value from Thousands of Miles, Thousands of Seats (Grade 5)
- Computational Fluency and Place Value from Implementation Guide
- Developing Computation Strategies That Make Sense from Number Puzzles and Multiple Towers (Grade 5)
- About the U.S. Standard Algorithm
The readings above are all published in Russell, S.J.; Economopoulos, K.; Wittenberg, L.; et al. Investigations in Number, Data, and Space®, Second Edition. Glenview: Pearson, 2012.
Common Core Alignment
The content in this session is aligned to the following Common Core State Standards and Math Practices:
MATH PRACTICES
MP1: Make sense of problems and persevere in solving them.
MP2: Reason abstractly and quantitatively
MP4: Model with mathematics
MP5: Use appropriate tools strategically
MP6: Attend to precision
Understanding structure of 100 and 1000:
MP4: Model with mathematics
MP5: Use appropriate tools strategically
MP6: Attend to precision
You may also wish to review the full set of Common Core State Standards in Math and/or videos of the Math Practices enacted in Investigations.
This chart was created by Bill McCallum in an attempt to provide some higher order structure to the practice standards, just as the clusters and domains provide higher order structure to the content standards.
MATH STANDARDS
Counting and Cardinality
Know number names and the count sequence.
- CCSS.Math.Content.K.CC.A.1 Count to 100 by ones and by tens.
- CCSS.Math.Content.K.CC.A.2 Count forward beginning from a given number within the known sequence (instead of having to begin at 1).
- CCSS.Math.Content.K.CC.A.3 Write numbers from 0 to 20. Represent a number of objects with a written numeral 0-20 (with 0 representing a count of no objects)
Count to tell the number of objects.
- CCSS.Math.Content.K.CC.B.4 Understand the relationship between numbers and quantities; connect counting to cardinality.
- CCSS.Math.Content.K.CC.B.4a When counting objects, say the number names in the standard order, pairing each object with one and only one number name and each number name with one and only one object.
- CCSS.Math.Content.K.CC.B.4b Understand that the last number name said tells the number of objects counted. The number of objects is the same regardless of their arrangement or the order in which they were counted.
- CCSS.Math.Content.K.CC.B.4c Understand that each successive number name refers to a quantity that is one larger.
- CCSS.Math.Content.K.CC.B.5 Count to answer “how many?” questions about as many as 20 things arranged in a line, a rectangular array, or a circle, or as many as 10 things in a scattered configuration; given a number from 1–20, count out that many objects.
Compare numbers.
- CCSS.Math.Content.K.CC.C.6 Identify whether the number of objects in one group is greater than, less than, or equal to the number of objects in another group, e.g., by using matching and counting strategies.1
- CCSS.Math.Content.K.CC.C.7 Compare two numbers between 1 and 10 presented as written numerals.
Operations and Algebraic Thinking
- Understand addition as putting together and adding to, and understand subtractions as taking apart and taking from (K)
- Represent and solve problems involving addition and subtraction (1 and 2)
- Understand and apply properties of operations and the relationship between addition and subtraction (1)
- Add and subtract within 20 (1 and 2)
- Work with addition and subtraction equations (1)
- Work with equal groups of objects to gain foundations for multiplication (2)
- Use the four operations with whole numbers to solve problems [in this case, addition and subtraction (4)]
K.OA.1-5
1.OA.1-8
2.OA.1, 2
3.OA.8
4.OA.3
Number and Operations in Base Ten
- Work with numbers 11-19 to gain foundations for place value (K)
- Extend the counting sequence (1)
- Understand place value (1 and 2)
- Use place value understanding and properties of operations to add and subtract (1 and 2)
- Use place value understanding and properties of operations to perform multi-digit arithmetic (3, 4 and 5)
- Generalize place value understanding for multi-digit whole numbers (4)
- Understand the place value system (5)
K.NBT.1
1.NBT.2abc
1.NBT.4-6
2.NBT.1ab, 2.NBT.5-9
2.MD.5
3.NBT.1
3.NBT.2
4.NBT.1-4
5.NBT.1
Activity 1: Mental Math
You will solve two mental math problems, one addition and one subtraction. You will examine strategies to identify the decomposing moves that occur implicitly. This activity will prepare you to examine the strategies the students employ in the video clips you will watch later in the session.
78 + 27
- Solve this problem mentally.
- Jot down your steps after you have solved the problem.
- After you have thought about your strategy, think about your first step.
Click the show link to see possible strategies for solving this problem.
| Adding by Place | Adding One Number in Parts | Making an Equivalent Problem |
|
|
|
Note: There are other possible variations for the final steps of each of these strategies.
Notebook
Reflect on the following questions in your notebook.
Compare your strategy with the strategies in the show. How is your strategy similar? …different?
Change and Compensate
In addition to the three strategies described in the “show” above, students use approaches that require compensation. These strategies also provide an opportunity to think about what numbers are decomposed. This strategy is similar to Making an Equivalent Problem.
Knowing landmark numbers and how to decompose and compose them are important to flexibly solve addition and subtraction problems (e.g., 78 is close to 80 and 75 is nested in 78).
For example:
| Changing the Numbers and Compensating |
78 + 27 I changed the 78 to an 80 and then subtracted 2. 78 + 2 = 80 (Changing to a landmark number, i.e. composing the 80) 80 + 27 = 107 107 – 2 = 105 (Adjusting the sum, since +2 and -2 are additive inverses) |
57 – 28
- Solve the problem mentally
- What was your first step?
See some possible strategies for solving this problem below.
Subtracting in Parts
- 57 – 28
- {28 = 20 + 7+ 1}
- 57 – 20 = 37
- 37 – 7 = 30
- 30 – 1= 29
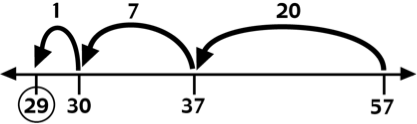
Subtracting by Place
- 57 – 28
- / \/ \
- 40 17 20 8
- 40 – 20 = 20
- 17 – 8 = 9
- 20 + 9 = 29
Changing the Numbers and Compensating
- 57 – 28
- {57 + 1 = 58}
- 58 – 28 = 30
- 30 – 1 = 29

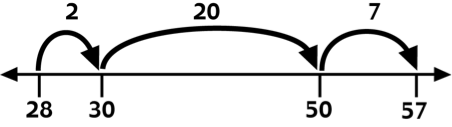
Adding Up
- 57 – 28
- (the distance is
composed as we
add up from
28 to 57) - 28 + 2 = 30
- 30 + 20 = 50
- 50 + 7 = 57
- 2 + 20 + 7 = 29
Creating an Equivalent Problem
- 57 – 28
- {57 + 2 = 59}
- {28 + 2 = 30}
- 59 – 30 = 29

Notebook
Reflect on the following questions in your notebook.
Compare your strategy with the strategies in the show. How is your strategy similar? …different?
Final Thoughts…
You have examined methods for solving addition and subtraction problems. As you solved these problems, you paid attention to how you were decomposing and composing the numbers you were working with so that you could operate in ways that were convenient and efficient. During the next part of this session, you will examine how students use decomposition strategies as they add and subtract.
Activity 2: – Students Solving Problems
You will view second and fourth grade students solving addition and subtraction problems. Their strategies involve decomposing numbers. As you watch the clips, pay attention to how the students break numbers apart in ways that make them easier to work with, and how this helps them solve the problems more efficiently.
In addition to the student work, you will hear the teacher commentaries on how they made decisions in the classroom and how they thought about questions they asked to push students’ thinking.
Note: The size of the numbers in the problems in the video are purposefully small so students can focus their strategies, making generalizations exploring how the operation(s ) and applying the flexible and efficient strategies to larger numbers.
Laura (Grade 2)
This clip shows Laura, a second grade student who has solved a story problem about 35¢ –16¢. Her teacher, Lisa, listens to her explanation, records her strategy and later shares her reflections.
Notebook
Reflect on the following questions in your notebook.
- What evidence did you see of Laura decomposing numbers?
- What does she understand about number relationships?
- What does she understand about the operation that helps her break numbers apart?
Click the show link to read other comments about Laura’s thinking.
- Laura used what she knew about money and coins when she decomposed the 35
- She could keep track of all the parts when she broke up the numbers
- She knew what parts to recombine to find her answer
Sean and Victoria (Grade 2)
Two students solve a subtraction story problem. The classroom teacher, Rose, shares her reflections.
Notebook
Think about the focus questions as you watch the clips. Record your thoughts in your notebook.
- What evidence did you see of each student decomposing numbers?
- What does each student understand about number relationships?
- What does each student understand about the operation that helps him or her break numbers apart?
Click the show link to read other comments about Sean’s and Victoria’s thinking.
Sean broke up the 17 to make it compatible to work with 39.
He paid attention to both numbers as he decomposed.
He used a subtracting-in-parts strategy and knew he had the answer when he had taken away all of the 17.
Victoria decomposed both addends by place value. She seemed to like working with tens and ones separately, and made groups of ten where she could. She was flexible moving back and forth between the tens and ones.
1,000 – 359
- Solve the problem mentally.
- Try out a strategy from the mental math we did in Activity 1 that is new to you.
- What was your first step?
Notebook
The following two video clips are of two different fourth grade students sharing their solution strategies to this problem. Think about the focus questions as you watch the clips and record your thoughts in your notebook.
- What evidence did you see of each student decomposing numbers?
- What does each student understand about number relationships?
- What does each student understand about the operation that helps him or her break numbers apart?
Use Anthony’s strategy to solve this new problem: 1,004 – 428.
Final Thoughts…
When students use these decomposing strategies they become more flexible problem solvers. Depending on the numbers and the operation in a problem, their decomposing strategies will vary. Knowing combinations and facts contributes to their ability to efficiently solve problems.
Activity 3: Practice
You are going to experience some activities that support practice with breaking numbers apart and putting them back together.
Roll-A-Square
You will examine a game called Roll-a-Square. In this game players take turns rolling dot cubes (or number cubes) and collecting interlocking cubes, snapping them together into rows of ten until they have ten rows of ten cubes and can form a 10-by-10 square. At the end of each turn players say the total number of cubes and look under the last cube to see if there is a question or direction on that square on the game board.
ScreenCast Directions for Roll-a-Square
Notebook
Reflect on the following questions in your notebook.
- How does this game support students in thinking about composing and decomposing numbers?
- How are students using counting skills?
- How does this game contribute to students’ understanding of place value?
- How does this game support the development of computational strategies?
Click the show link to see how Roll-a-Square supports the development of computational fluency.
- Grouping by tens and ones
- Seeing that 100 is composed of 10 groups of 10
- Calculating the difference between a number and a multiple of 10
- Practicing addition combinations
Games like Roll-a-Square give students practice visualizing the structure of 100 that they can draw upon when solving problems. Think about the strategies that Victoria used to solve 48 + 25 and how that would look using cubes on a 100 chart making rows of ten.
Variations
The variation of this game is called Unroll-a-Square. Players start with 100 cubes on the board and remove the amount rolled. The strategy that Sean used to solve 39 - 17 can also be visualized on the 100 chart, starting with 39 cubes and then taking nine away from one row and eight away from the next row. First graders also play a game called Roll Tens.
Roll-A-Square Game Rules and Game Board
Close to Games
There is a sequence of related games throughout the grades that are Close To Games. These games are an opportunity for students to develop ideas about number relationships, the operations and computation strategies.
The goal of these games is to produce a sum as close to 100 (or 1,000) as possible. You may go over or under. Your score is the difference from 100. For example: If you had a choice between a sum of 97 and 101 (or 997 and 1,001) which one is the best choice to get the lowest score?
Close to 100
Watch the following screencast to see five rounds of Close to 100.
Close to 1,000
Directions
Deal out eight cards; choose six of the cards to create two three-digit numbers.
Let’s play a sample round of the game of Close to 1,000.
As you play, consider:
- How are you thinking about hundreds, tens and ones?
- How did you employ decomposing and composing strategies?
Suppose these are the cards you have drawn:
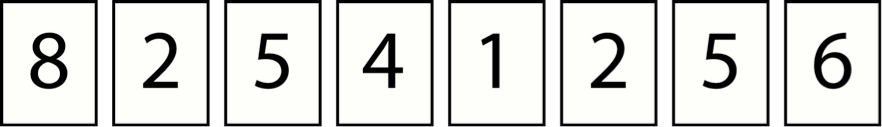
Make two three-digit numbers that when added together will get you as close to 1,000 as possible.
Click the show link to compare your strategy with others.
| Strategy | Rationale |
| 481 + 522 = 1,003 | Making 900 in the hundreds and 100 in the tens forces you to make the smallest number in the ones. this is a good move because we had a 2 and a 1. |
| 862 + 142 = 1,004 | Making 900 in the hundreds and 100 in the tens works best if you have number cards that will give you a low sum in the ones place. |
| 852 + 146 = 998 | Making 900 in the hundreds and a 90 in the tens forces you to try to make a sum in the ones as close to 10 as possible. |
Notebook
As you play, consider:
- Record your solution(s).
- How did the specific numbers on these cards affect your strategy?
- How were you thinking about how to compose the number 1,000?
Record your responses in your notebook
You will need the following materials for the next activity.
- Close to 100 and Close to 1,000 Game Directions and Recording Sheet
- Digit Cards
Use your paper digit cards to play five rounds of either Close to 100 or Close to 1,000. Record your solutions on the recording sheet.
Note: As students play games such as Close to 100 and Close to 1,000, they are considering how the place value of a digit affects the combinations they look for. Thinking about how a number such as 1,000 can be decomposed into two numbers allows students to develop a deeper understanding of the structure of the base-ten number system.
Notebook
Reflect on the following questions in your notebook.
- How did what you know about the base ten number system and decomposing numbers affect your strategy?
- How does this game contribute to students’ understanding of place value?
- How do the Close To games – support students’ development of computation strategies?
Observing Students
The fifth grade students in the following video have played Close to 100 and Close to 1,000 in earlier grades. This is evident in the way this one student solves the problem 1,456 – 568. He uses the number line as a tool to show his mental calculations.
Note: Representations and contexts are fundamental as students are developing computational fluency. They are the mental images that allow students to see how the operations work.
Broken Calculator
Broken Calculator is a variation of the Today’s Number Ten-Minute Math activity in Grade 4. In this variation, students work to make a number appear on their calculator display without using particular keys, which are said to be “broken.” The broken keys can be operations, numbers, or both.
You will need a calculator.
Imagine that the 3 key and the 5 key are broken on your calculator.
How can you make the calculator display 35?
Notebook
Record your solutions.
Click on the show link to see other possible solutions.
Solutions might include:
29 + 6 76 – 41 100 – 60 - 5 4 x 9 – 1
Answer the following questions in your notebook.
- What do children have to know about decomposing numbers to justify that these expressions are equal?
- How does Broken Calculator support students in thinking about composing and decomposing numbers?
- How can it help them develop flexibility in solving problems?
Broken Calculator, like other Ten-Minute Math activities and Classroom Routines, offers a place for ongoing practice and can be modified depending on what students need to work on. Try Broken Calculator with different restrictions.
Notebook
Record your thoughts in your notebook.
- What does it mean to be computationally fluent with the operations of addition and subtraction at your grade level?
- What role does understanding place value play in ensuring that students efficiently, accurately and flexibly solve addition and subtraction problems?
- How does playing games, such as the ones you’ve just experienced, help students solve addition and subtraction problems efficiently, accurately and flexibly?
Activity 4: Connection to the U.S. Standard Algorithm
Session Summary
In this activity you will learn how starter problems and cluster problems help students develop flexible strategies for whole number computation. You will look for evidence of the CCSS (Content and Mathematical Practices) as you look at student work, watch students at work and read classroom cases.
Session Focus
In this activity you will:
- Examine the connection between students strategies and the U.S. Standard Algorithm
- Experience Cluster Problems to understand how they help students develop flexible strategies
- Examine and sort student work according to the CCSS Math Content Standards
- Make connections between the development of computational fluency in the elementary grades and the CCSS Content Standards and the Standards for Mathematical Practice
Getting Started: Connecting to the U.S. Standard Algorithm
Watch these 4th grade students’ explain the connection between a notation showing partial sums and one showing the U.S. Standard Algorithm for addition.
Read
About the U.S. Standard Algorithm
These Teacher Notes focus on the U.S. Standard Algorithms (addition, subtraction and multiplication).
Notebook
Reflect on the following questions in your notebook.
- What do the students in the video and readings understand about the place value?
- What do the students understand about the operations?
- What prior work might the students have done that so assure their understanding of how the algorithm works? (Think about the math you have experienced, as well as the math you observed or read about students doing (K-5) during this course.)
Final Thoughts…
“If students are challenged to explain the reasoning (MP2) behind the variety of strategies that they use to solve multi-digit calculation problems and if they learn to pay attention to the structure (MP7) that they employ in these strategies, then the step to work the conventional algorithm is not such a great leap.
There may be some notational differences, but those algorithms are based on the same structures that the students have already encountered.”
Deborah Schifter
NCSM 2013
Discussion
- What question(s) did this session raise for you about your students’ work on decomposing numbers and how it contributes to their computational fluency? Indicate your grade level in your post.
- Think about the experiences in this session. In what ways did you or might students use the following Mathematical Practices? Be specific. Cite examples. (When you respond, include the Mathematics Practice you are sharing in the title of your response e.g., MP 7 Video (name the video clip) or MP6 (name the activity).
- Math Practice 4: Model with mathematics
- Math Practice 5: Use appropriate tools strategically
- Math Practice 7: Look for and make use of structure
Remember to post early and return to the discussion forum throughout the week to read and respond to others’ posts.
Key Learning
- Decomposing numbers contributes to students’ development of computational fluency.
- Mental math helps students develop strategies for breaking numbers apart to solve multi-digit arithmetic problems.
- Describing, analyzing, and comparing strategies is an important part of the work students do to develop strategies they can apply efficiently and flexibly to solve more complex problems.
- The inverse relationship between addition and subtraction is highlighted as students break numbers apart.
- Understand that place value is inherent in the decomposition of numbers and use it to solve problems.
- Games, Classroom Routines and Ten-Minute Math provide students necessary practice breaking numbers apart to efficiently perform multi-digit arithmetic.
Representations and contexts are fundamental as students are working on computational fluency. They become mental images of how the operations work.
Notebook
Fill out the Session 3 Notebook Page to reflect on your own learning and record ideas that you want to remember and/or try with students.
Select the following links to go to the Notebook.
- Session 3: Overview
- Session 3: Activity 1
- Session 3: Activity 2, Laura
- Session 3: Activity 2, Sean & Victoria
- Session 3: Activity 2, Sam & Anthony
- Session 3: Activity 3, Roll-A-Square
- Session 3: Activity 3, Close to 1,000
- Session 3: Activity 3, Broken Calculator
- Session 3: Activity 3, Final Reflection