Overview
Session Summary
In this session you will examine how children make sense of the operation of division and develop strategies for solving division problems. You will engage in mental math by estimating the answers to division problems; explore contexts for division problems including interpreting remainders in context; examine strategies for solving division problems; and view video clips of students sharing their division strategies.
Session Focus
In this session you will:
- Consider what students need to know in order to divide
- Consider contexts that support understanding the meaning of division
- Examine strategies that students use to solve division problems
- Examine the foundations for computational fluency when using the operation of division
Getting Started: Closest Estimate
Closest Estimate is a Ten-Minute Math activity from Grades 4 and 5. You will look at a problem and possible estimates.
371 ÷ 6 ≈ 6 60 600
- Which is the closest estimate?
- How did you make your estimate?
- How did you determine the magnitude of your answer?
Click the show link to see the estimates that other participants have shared.
- I know that 6 x 6 = 36, and 6 x 60 = 360, and that is very close.
- 6 x 600 = 3,600, which is too high, so it has to be 60.
- I thought of a context, 371 cookies shared by 6 people. There are less than 600 cookies to start, so each person can’t get 600. If each person got 6, there would still be many cookies left to give out. So the answer is 60.
Is the actual answer more or less than 60? How do you know?
641 ÷ 35 ≈ 10 15 20
- Which is the closest estimate?
- How do you know?
- How did you make your estimate?
- If you changed the numbers, how did you change them, and why?
Click the show link to see examples of student responses.
- I knew that 35 x 10 = 350, and twice that is 700, so 20 was it
- I rounded both numbers down: 600 ÷ 30 = 20, so that was my estimate
- I didn’t know whether 15 or 20 was closer, so I thought of 15 x 35 as (20 x 35) – (5 x 35) which is 700 – 175 = 525. 700 is closer to 641 than 525, so 20 is the closest estimate
Is the actual answer more or less than 20? How do you know?
Note: As students explain why it is less than 20, they might justify it using:
- 35 x 20 = 700; 700 is 59 more than 641, so it has to be less than 20, but pretty close
- 20 x 30 would be 600 and 5 more 20s would be 100, and 100 plus 600 would be more than 641
Observing Students
This video shows students in a fifth grade class working on the Ten-Minute Math activity, Closest Estimate.
The 5th grade students in this video use multiplication to select the closest estimates. They notice the magnitude of their estimates, and share how they broke numbers apart to arrive at their estimates.
In this session you will see how these estimation strategies relate to the ways that students make sense of division and solve division problems.
Readings
Two Kinds of Division: Sharing and Grouping from Equal Groups (Grade 3)
What Do You Do With the Remainders? From How Many Packages? How Many Groups? (Grade 4)
How Many Teams? from How Many Packages? How Many Groups? (Grade 4)
Division Strategies from Number Puzzles and Multiple Towers (Grade 5)
Division Notation from How Many People? How Many Teams? (Grade 5)
Naming Division Strategies from How Many People? How Many Teams? (Grade 5)
Representations and Contexts for Mathematical Work from Implementation Guide K-5
The readings above are all published in Russell, S.J.; Economopoulos, K.; Wittenberg, L.; et al. Investigations in Number, Data, and Space®, Second Edition. Glenview: Pearson, 2012.
Activity 1: Division Contexts
In this activity, you will experience the ideas of number of groups and number in each group in the context of teams. You will solve a division problem, write a story context for the problem and consider whether the same story can fit both problems. You will also examine remainders and how the story context affects the solution. You will use your division contexts to highlights two models of division: sharing and grouping. While it isn’t important that students learn to recognize the difference between sharing and grouping situations, it is important that they can move flexibly between the two. The problems and representations below illustrate the two models of division.
Sharing I have 18 balloons and two people.
How many balloons does each person get?

Grouping I have 18 balloons to put into bunches of two.
How many bunches will there be?

Read
Read Two Kinds of Division: Sharing and Grouping.
In division, we think about counting the number of groups and counting the number in each group. Counting prepares children for solving division problems. In grades 4 and 5, many of the story problems are about players and teams. These contexts are ones that children relate to and understand easily. The contexts in Investigations are kept consistent so that children use them as anchors to refer back to when thinking about and solving problems.
Read Representations and Contexts for Mathematical Work.
Story Problem
Using representations and contexts can help us construct a clearer understanding of an operation and the number relationships involved as we compute. In earlier sessions you’ve seen how the number line can be a useful representation for understanding addition and subtraction strategies, and how arrays can serve as a model for multiplication. Now as we focus on the operation of division, you will use context as the structure for understanding the action of division.
Write two story problems for 74 ÷ 6. (a grouping story problem and a sharing story problem).
- Explain what the 6, the 74 and the quotient mean in each story context.
- How are the two situations different?
- Describe what you would do with the remainder, if there is one in your context.
- Share your stories in the Division Story Forum.
Click the show link to see an example of grouping and an example of sharing.
The school cafeteria baker made 74 cookies. She put 6 cookies in each bag. How many bags did she fill? (grouping–how many equal groups?)
There are 74 children in summer camp. There are 6 counselors, each leading one team of the same size. How many children are in each team? (sharing–how many are in each group?)
Six could be the number in each group or the number of groups
Here is an example using the array you learned about in the multiplication session.
I have 74 carpet tiles to arrange on the floor. I’m going to put 6 tiles in each row. I want to use as many tiles as I can. What will be the dimension of my carpet?
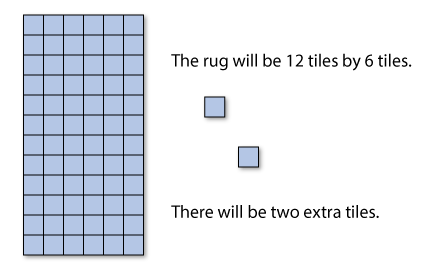
Splitting the Dividend
The following is an example of splitting the dividend to find the quotient of 74 ÷ 6.
Use groups of the divisor (for example, starts with 10 groups of 6)
- Break the dividend 74 into 60 + 14
- Start with 10 groups of 6. Why 10?
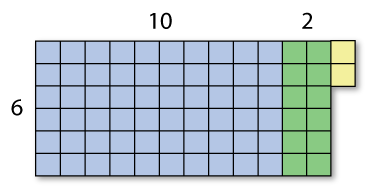
Students may say:
6 x 10 = 60, so 60 ÷ 6 = 10
6 x 2 = 12, so 14 ÷ 6 = 2 with 2 tiles left over
I can make 12 groups of 6 with two tiles left over.
74 ÷ 6 = 12 r 2
Others starting points for 74 ÷ 6
Students may:
- Start with 5 groups of 6
- Start with 11 groups of 6
- Start with 6 groups of 6
Remainders
What does the 2 or R2 mean?
What do you have to do with the 2 to answer the problem posed in your story context?
Depending on the question you are trying to answer, the remainder affects the answer in different ways. For example, in the story about the cookies the question was, “How many bags did she fill?” The answer is 12 bags. The 2 cookies left over are not in the bags she filled.
If the question had been “How many bags does she need to pack all her cookies?” the answer would have been 13 bags. She would have needed one more bag for the remaining 2 cookies. (This is assuming that the bags only fit 6 cookies. If they fit more you could still have 12 bags but two of those bags will have 7 cookies and 10 will have 6.)
Not all contexts have remainders. Think about the following contexts: time, money, measurement, food, object (balloons) or people.
Note: Students may at first write equations such as 74 ÷ 6 = 12 R2 to indicate their answer to the division problem this notation, however, is not correct mathematically because “12 R2” does not indicate a number (i.e., it cannot be placed on a number line). For example, the answer to 74 ÷ 6, expressed as 12 R2, can be interpreted as 12 groups of 6 plus 2 from the next 6.
However, 122 ÷ 10 also gives an answer of 12 R2, which now represents 12 groups of 10 plus 2 from the next 10. Even though both answers can be expressed as 12 R2, 74 ÷ 6 and 122 ÷ 10 are not equivalent. When students use fractions to express a quotient, they can use the equation format, for example, 74 ÷ 6 = 12 2/6 and 122 ÷ 10 = 12 2/10.
Steer students away from using the “R” notation as part of an equation as it encourages the interpretation of the equals sign as meaning “now write the answer” rather than as indicating equality. When they use the division “box” notation, they can write 31 R2 on top of the box; they can also just write 31 R2 separately as the result of their calculations.
In the next activity, you will continue to examine the operation of division as you focus on the strategies that you – and children – use to solve division problems.
Activity 2: Division Strategies
In this activity, you will solve a division problem. The context for the problem is counting around the room, a familiar activity for K-5 teachers. The focus is on naming the division strategies.
Counting Around the Class
Counting Around the Class starts in Kindergarten, when children are counting by 1, and continues throughout the grade levels.
Watch the fourth graders in the following video to get an image of Counting Around the Class. Notice the teacher asking, “How many people have said a number? How do you know?”
Ms. Chen's fifth graders have been counting around the class by different numbers. On this day she poses the following question:
“There are 32 students in our class. When we count by a certain number, the last student says 1,280. If each of you says only one number, by what number are we counting?”
Notebook
Solve the problem. Record your strategies in your notebook.
Examine the accordion below to see strategies that could be used to solve this problem.
Using groups of the divisor
- 1,280 ÷ 32
- 32 x 2 = 64
- 64 x 2 = 128 (that’s 4 x 32)
- 128 x 10 = 1,280 (4 x 32 x 10 = 40 x 32)
- 1,280 ÷ 32
- 32 x 10 = 320
- 32 x 20 = 640
- 32 x 40 = 1,280
- 1,280 ÷ 32
- 32 x 4 = 128
- 32 x 40 = 1,280
Breaking the dividend into parts
- 1,280 ÷ 32
- 1,280 = 640 + 640
- (640 ÷ 32) + (640 ÷ 32)
- = 20 + 20
- = 40
- 1,280 ÷ 32
- 1,280 = 960 + 320
- (960 ÷ 32) + (320 ÷ 32)
- = 30 + 10
- = 40
Making an equivalent problem
- 1,280 ÷ 32
- Dividing both numbers by 4:
- 1,280 ÷ 32 = 320 ÷ 8 = 40
- 1,280 ÷ 32
- Halving both numbers repeatedly:
- 1280 ÷ 32
- = 640 ÷ 16
- = 320 ÷ 8
- = 160 ÷ 4
- = 80 ÷ 2
- = 40 ÷ 1
- = 40
Solving an easier, related problem and then compensating
- 1,280 ÷ 32
- 50 x 32 = 1,600
- 1,600 – 1,280 = 320
- 320 ÷ 32 = 10
- 50 – 10 = 40
Students will use different strategies to solve division problems. Their strategies rely on the relationship between multiplication and division, breaking problems into smaller more manageable parts, and using what they know to find out what they don’t know.
The contexts in the stories help them keep track of the parts of the problem they have solved and in determining the final answer.
Activity 3: Starter Problems
You will mentally solve a division problem, watch video of grade 5 students sharing their division strategies and examine student work examples of students solving the problem 1,564 ÷ 36.
Read
EQUITY MOMENT
Some people feel overwhelmed doing mental math and it can be difficult to focus on the problem. We encourage you to mentally solve 159 ÷ 13, but if a mental strategy doesn’t feel comfortable feel free to solve it any way you wish, including paper-and-pencil strategies. Then try a new strategy.
159 ÷ 13
- Mentally solve the problem.
- Think about your strategy.
- Record your steps.
- Try a different strategy (see Activity 2).
- How are the strategies similar? How are they different?
Students Solving Division Problems
You will watch Thomas and Elaine solving this same problem. As you watch these students, pay attention to the strategies they are using to solve the division problem.
Videos
Notebook
Take notes while you view the students.
Write the steps of the students’ method to be sure you understand the logic of the approach.
Based on the strategies the students use, what does he/she understand about the operation of division?
Click the show link to review a few important ideas about these students’ strategies.
Each of the students has used a different strategy:
Thomas is breaking the dividend into parts. He solves it as a sharing situation. Elaine finds groups of the divisor, multiplying up by 13’s to 159.
While the representation of Thomas’ strategy appears cumbersome, his strategy is efficient as illustrated below.
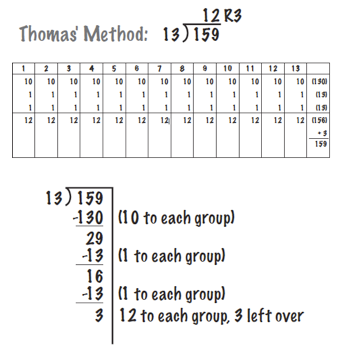
Students often use multiplication to solve this problem.
What do students need to understand in order to solve division problems this way?
500 ÷ 16
Notebook
Solve the problem.
Jot down your thinking in your notebook.
How would you solve 500 ÷ 16, by starting with 20 x 16?
Notice that the teacher begins by saying 20 ÷ 16. However, she means 20 x 16 and that is what is written on her chart paper.
Notebook
In what way did starting by 20 x 16 help students?
What did the teacher do to promote thinking?
Final thoughts…
By the end of fifth grade our benchmark for students is that they “solve division problems efficiently.” They are given the problem 1,564 ÷ 36 as an assessment. In their work we are looking that they can:
- break the problem into easily manageable parts,
- keep track of what has been solved and what remains to be solved,
- use their partial solutions to find the solution to the original problem,
- present their solutions clearly and concisely.
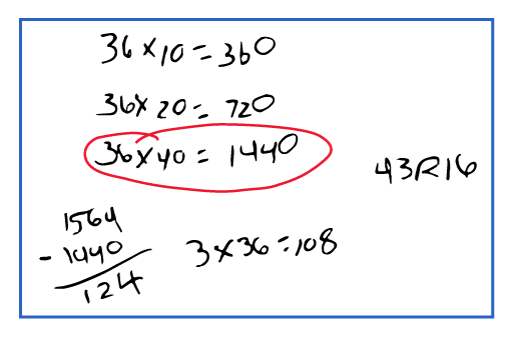
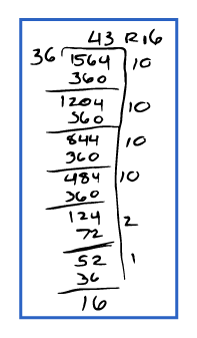
Shandra uses a strategy that is similar to Elaine’s. She begins multiplying by 10 and then quickly works her way up to 36 x 40. Perhaps she grouped 36s mentally and determined that 3 x 36 would get her as close as she could to 124.
Walter’s strategy is similar to Thomas’. Walter repeatedly subtracts 10 groups of 36 until he is at 124. Although he gets the correct answer, he is not solving the problem efficiently. At this point in grade 5 students should be able to handle larger, and thus fewer, groups of the divisor. We might ask Walter, “What is the largest group of 36 you can take without going over 1,500?” or “If 10 x 36 is 360, what is 20 x 36?”
Discussion
Session 5 Discussion Forum
How does the relation between multiplication and division help students understand division and help them develop efficient strategies?
In what ways do contexts and representations support students’ understanding the meaning of division?
Division Story Problems Share Forum
Share your division stories from Activity 1 here. You can write and illustrate the problem on paper, take a picture of the work and upload it into the forum.
Read and respond to other participant stories.
Remember to post early and return to the discussion forum throughout the week to read and respond to others’ posts.
Common Core Alignment
The content in this session is aligned to the following Common Core State Standards and Math Practices:
MATH PRACTICES
MP1: Make sense of problems and persevere in solving them.
MP2: Reason abstractly and quantitatively
MP5: Use appropriate tools strategically
MP6: Attend to precision
MP8: Look for and express regularity in repeated reasoning.
You may also wish to review the full set of Common Core State Standards in Math and/or videos of the Math Practices enacted in Investigations.
This chart was created by Bill McCallum in an attempt to provide some higher order structure to the practice standards, just as the clusters and domains provide higher order structure to the content standards.
MATH STANDARDS
Operations and Algebraic Thinking 3.OA, 3.OA.1, 2, 3, 4, 5, 6, 7, Represent and solve problems involving multiplication and division.
- Interpret whole-number quotients of whole numbers, e.g., interpret 56 ÷ 8 as the number of objects in each share when 56 objects are partitioned equally into 8 shares, or as a number of shares when 56 objects are partitioned into equal shares of 8 objects each. For example, describe a context in which a number of shares or a number of groups can be expressed as 56 ÷ 8.
- Use multiplication and division within 100 to solve word problems in situations involving equal groups, arrays, and measurement quantities, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem.
- Determine the unknown whole number in a multiplication or division equation relating three whole numbers. For example, determine the unknown number that makes the equation true in each of the equations 8 × ? = 48, 5 = ? ÷ 3, 6 × 6 = ?.
Understand properties of multiplication and the relationship between multiplication and division.
- Apply properties of operations as strategies to multiply and divide. Examples: If 6 × 4 = 24 is known, then 4 × 6 = 24 is also known. (Commutative property of multiplication.) 3 × 5 × 2 can be found by 3 × 5 = 15, then 15 × 2 = 30, or by 5 × 2 = 10, then 3 × 10 = 30. (Associative property of multiplication.) Knowing that 8 × 5 = 40 and 8 × 2 = 16, one can find 8 × 7 as 8 × (5 + 2) = (8 × 5) + (8 × 2) = 40 + 16 = 56. (Distributive property.)
- Understand division as an unknown-factor problem. For example, find 32 ÷ 8 by finding the number that makes 32 when multiplied by 8.
Multiply and divide within 100.
- Fluently multiply and divide within 100, using strategies such as the relationship between multiplication and division (e.g., knowing that 8 × 5 = 40, one knows 40 ÷ 5 = 8) or properties of operations. By the end of Grade 3, know from memory all products of two one-digit numbers.
Number and Operations in Base Ten 4.NBT, 4.NBT.3, 5, 6, Generalize place value understanding for multi-digit whole numbers.
- Use place value understanding to round multi-digit whole numbers to any place.
Use place value understanding and properties of operations to perform multi-digit arithmetic.
- Find whole-number quotients and remainders with up to four-digit dividends and one-digit divisors, using strategies based on place value, the properties of operations, and/or the relationship between multiplication and division. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.
Number and Operations in Base Ten 5.NBT, 5.NBT6, Understand the place value system.
- Find whole-number quotients of whole numbers with up to four-digit dividends and two-digit divisors, using strategies based on place value, the properties of operations, and/or the relationship between multiplication and division. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.
Key Learning
Student need to:
- understand that division is about equal-sized groups
- break the problem into easily manageable parts to efficiently solve division problems
- use contexts for a division problem - including both sharing and grouping situations
- find quotients using strategies based on place value, the properties of operations and/or the relationships between multiplication and division
- understand that while you can break numbers apart, for division it’s different than for multiplication
- use equations and arrays to explain their strategies
- know that the remainder impacts the answer in story problem contexts
Notebook
Fill out the Session 5 Notebook Page to reflect on your own learning and record ideas that you want to remember and/or try with students.
Select the following links to go to the Notebook.