Overview
Session Summary
In this session you will learn how starter problems and cluster problems help students develop flexible strategies for whole number computation. You will look for evidence of the CCSS (Content and Mathematical Practices) as you look at student work, watch students at work and read classroom cases.
Session Focus
In this session you will:
- Examine the connection between students strategies and the U.S. Standard Algorithm
- Experience Cluster Problems to understand how they help students develop flexible strategies
- Examine and sort student work according to the CCSS Math Content Standards
- Make connections between the development of computational fluency in the elementary grades and the CCSS Content Standards and the Standards for Mathematical Practice
Getting Started: Connecting to the U.S. Standard Algorithm
Algorithms are step-by-step procedures. The U.S. Conventional algorithm for multiplication is one that has traditionally been taught in the United States. Other places in the world use different algorithms. The partial product method you experienced in Session 1 is an algorithm as well. Some English Language Leaners may come from places where other standard algorithms for multiplication are used.
Two Algorithms: What do they mean?
In both algorithms* recorded below, the problem, 142 x 36, is solved by breaking the numbers apart by place.

Look closely at the solutions and make sense of what the notation shows.
Record the solution to 138 x 24 using Solution 1 and Solution 2
Notebook
Respond to the following questions in your notebook.
- How would you explain to someone else what the numbers in each solution show? What do the small 1’s and the small 2 in Solution 2 mean?
- How are these two notations different from each other? How are they the same?
Some points that could emerge from the discussion are*:
- Both algorithms are place-value strategies. As students compare the two algorithms side by side, students should notice that the first partial product in Solution 2 is 852, the product of 142 x 6. This is equal to 600 + 240 + 12 (the products of 100 x 6; 40 x 6; and 2 x 6) shown in solution 1. The same is true for the other partial products.
- The notation for Solution 2 combines multiplying and adding of partial products. Solution 2 is an example of the U.S. Standard Algorithm and was invented to save space and steps.)
- The notation of Solution 1 is more transparent than that of Solution 2. It is clear in the notation what each step is, and the full value of the numbers is written each time (e.g., 100 x 30 = 3000). In Solution 2, some of the steps are hidden by “carrying” numbers and by either moving over a space for the 2nd partial produce or write in a 0. Thus, Solution 2 provides an example of notation that is concise but not necessarily clear.
- In Solution 2, you have to start at the right and work toward the left, following the steps exactly. In Solution 2, you can calculate the partial products in any order, as long as you keep track of the parts.
Read
About the U.S. Standard Algorithm
These Teacher Notes focus on the U.S. Standard Algorithms (addition, subtraction and multiplication).
Notebook
Reflect on the following questions in your notebook.
- What prior experiences do students need to understand how the multiplication algorithm works? (Think about the math you have experienced in this course, as well as what you observed students doing in the videos and reading.)
Final Thoughts…
“If students are challenged to explain the reasoning (MP2) behind the variety of strategies that they use to solve multi-digit calculation problems and if they learn to pay attention to the structure (MP7) that they employ in these strategies, then the step to work the conventional algorithm is not such a great leap.
There may be some notational differences, but those algorithms are based on the same structures that the students have already encountered.”
Deborah Schifter
NCSM 2013
Readings
Computational Fluency and Place Value from Implementation Guide
Developing Computation Strategies That Make Sense from Number Puzzles and Multiple Towers (Grade 5)
Reasoning and Proof in Mathematics from Multiple Towers and Division Stories (Grade 4)
Readings About the U.S. Standard Algorithm
Why Study the U.S. Conventional Algorithms? from Landmarks and Large Numbers (Grade 4)
Working with the U.S. Algorithm from Thousands of Miles, Thousands of Seats (Grade 5)
Studying The Algorithm from Number Puzzles and Multiple Towers (Grade 5)
Computational Algorithms and Methods from Implementing Investigations
Readings About Starter and Cluster Problems
About Cluster Problems from How Many Packages? How Many Groups? (Grade 4)
Multiplication Clusters and the Properties of Multiplication from Multiple Towers and Division Stories (Grade 4)
Classroom Cases
The following cases appear in the Implementation Guide at the respective grade.
The Case of Ellen: Deciding What to Nudge (Grade 3)
The Case of Kyle and Asiah: Multiplying by Multiples of 10 (Grade 4)
Activity 1: Related and Cluster Problems
Cluster problems provide students different starting points to solve a problem. Students break up the problem using related problems. Students are given a few problems (a cluster). The problems in the cluster often are ones that students can mentally solve. Many involve landmarks such as multiples of ten or solving half of the problem and doubling that product.
Introducing the Cluster Problem 46 x 25
Solve the problem using one or more of the starter problems.
| 46 x 25 | |
4 x 25 40 X 25 |
10 x 25 50 X 25 |
Listen to the teacher, as she introduces the cluster problem (shown below) to her students.
Nashaya’s Strategy
Watch Nashaya share her strategy.
Notebook
After viewing the video, reflect on the following questions in your notebook.
- What does Nashaya understand about the base-ten number system?
- What property did Nashaya use when she solved the problem?
Stephen
Stephen successfully solved this problem one way. He realized his second way was incorrect. He chose 4 x 25 as his first step and continued using the following related problems: 4 x 25, 10 x 25, 6 x 25.
As you watch Stephen explain his thinking, jot down his steps.
Why is Stephen incorrect? What did Stephen learn from his error?
Stephen shares his incorrect steps and how listening to Nashaya helped him see his error.
Notebook
In your notebook, record your reflections on the following questions:
- Where do you see evidence of students looking for and making use of structure such as place value and the properties of operations? (Math Practice 7)
- Where do you see evidence of students constructing viable arguments and critiquing the reasoning of others, that is, explain the reasoning underlying a strategy or solution? (Math Practice 3)
Practicing Cluster Problems
| Use one or more of the following related problems to solve 42 x 19. | |
42 x 10 = 42 x 5 = |
42 x 2 = 42 x 20 = |
| Use one or more of the following related problems to solve 450 ÷ 16. | |
|
160 ÷ 16 = 80 ÷ 16 = |
320 ÷ 16 = 16 x 10 = |
Read
Developing Computational Strategies That Make Sense.
Notebook
In your notebook, record your reflections on the following question:
- In what ways do cluster problems support students’ development of computational fluency?
Activity 2
You will examine samples of student work and determine where they fall according to CCSS Math Content Standards. The purpose of this activity is to understand how related content standards develop across grades.
Looking at Student Work
Look at the student work across the grades and use the CCSS Math Content Standards to think about the critical phases in the progression for number and operations across the grades.
Multiplication and Division
The following student work samples represent the types of problems students are solving and how students represent their strategies in print. Look closely at the work from 2nd to 5th grade. Respond to the following questions in your notebook.
- How do the ideas of multiplication and division progress across the grades? (Cite examples from either the work or from your experiences in previous sessions in this course.)
- What ideas are critical for students to understand how the U.S. Standard Algorithms for multiplication and division work?
- In what ways will the experiences in the lower grades help students develop a solid understanding of the U.S. Standard Algorithm for multiplication?
- What generalizations will students make about multiplication and division that they can later apply beyond whole number computation situations?
Multiplication and Division Content Standards 2-5 Table
Multiplication and Division Student work
Click on the student work to enlarge the work.
| Multiplication and Division | |||||
|---|---|---|---|---|---|
| 5th |  |
 |
 |
 |
|
| 4th |  |
 |
 |
 |
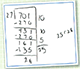 |
| 3rd |  |
 |
 |
 |
|
| 2nd |  |
 |
 |
||
Notebook
Use the student samples and descriptions of the CCSS grade level standards to craft your own description of how the ideas progress across the grades.
Cite specific examples. You may want to refer back to video clips or readings from previous sessions.
Activity 3
In this activity you will delve more deeply into the Mathematical Practices (MP). You will examine video and/or classroom cases for evidence of MP.
Bringing Math Practices to Life in the Classroom…
(adapted from http://investigations.terc.edu/curriculum_clrm/mathpracticestandards.cfm)
The teacher, the student, and the curriculum each have a role to play in making a classroom, that embodies the Standards for Mathematical Practice come to life.
The curriculum presents a sequence of tasks designed to focus on particular content standards and to foster the use of the Math Practices. When looking at a particular task, questions to think about include:
- What kind of task is it?
(e.g., a decontextualized computation problem, a problem set in a context, a problem with more than one answer) - What math does the task focus on?
- Does the task suggest the use of one or more MPs? In what ways do the MPs support students’ mathematical thinking and understanding of the math content?
Teachers must be able to see and recognize the various Math Practices, and they must be “mathematically proficient.”
- use their knowledge of the math, their students, and the curriculum to implement the curriculum.
- facilitate the creation of an environment in which the Math Practices can flourish.
- sometimes they purposefully focus on one particular Math Practice; other times, they capitalize on an opportunity that arises in the classroom.
Students are the critical piece of the puzzle. Where they are with an idea (developmentally and mathematically) and how they approach a problem affects how they employ the Math Practices. It’s important for all students to:
- - making sense of quantities and relationships
- - create a representation of the problem
- - apply prior knowledge
- - check to see if the solution is accurate
- - look for patterns and structure
- - communicate and defend reasoning using contexts, math tools and/or drawings
The teacher, the student, and the task each have a role to play. Successful implementation of the Standards for Mathematical Practice relies on the interaction of these three factors. A task might be rich and complex, but if students aren’t ready for the ideas or it’s taught very procedurally, it won’t result in deep and varied use of the Practices. On the other hand, what can seem like a simple computation problem can blossom into a rich and interesting task.
Examining Classroom Vignettes
In this activity you will examine classroom vignettes, (either video and/or classroom cases) for evidence of teacher moves/practices, student learning, the purpose of the task and identifying instances of specific CCSS Mathematical Practices (indicated on the table below). You will share your findings on the Vignette Discussion Board.
Choose at least two artifacts (video and/or a case).
For each vignette:
- Read the case or view the video several times, focusing each time on either the teacher, students, task(s) and/or MP.
- Respond to the following questions in your notebook after you read the case or view the video.
- What do you notice about what the teacher does (e.g., questions the teacher asks, the structure of the math experience and classroom environment)?
- What are the students doing and saying? How are they thinking about the relationship between the numbers in the problems and a strategy they can easily and accurately use?
- How did the experience engage students and help them understand the meaning of the operation(s)?
- What evidence in the case or video is there of the specific MP’s listed on the table?
- Go to the Vignette Discussion to share your overall findings for each of the Vignettes you examined.
| Classroom Cases | MP |
| The Case of Ellen: Deciding What to Nudge (Gr 3) | 1,5 |
| The Case of Kyle and Asiah: Multiplying by Multiples of 10 (Gr 4) | 1,3,6,7 |
| Videos | MP |
| Multiple Towers | |
| Ryshawn and Nicholas 4 x 29 (Gr 3) (Session 1 Multiplication, Activity 3) |
1, 7 |
| Jemea 29 x 12 (Gr 5) (Session 1 Multiplication, Activity 3) |
3, 6, 7 |
| Building Flexibility with Cluster Problem (Gr 4/5) (Session 6 - Click on Activity 1 tab at the top of this page)
|
1, 3, 7, 8 |
Discussion
Choose one Mathematical Practice (MP). Describe how the MP contributes to students’ computational fluency. Give examples from you personal experience or experiences from this course.
Share a take-away about computational fluency that you will integrate into your practice.
Remember to post early and return to the discussion forum throughout the week to read and respond to others’ posts.
Common Core Alignment
The content in this session is aligned to the following Common Core State Standards and Math Practices:
MATH PRACTICES
MP1: Make sense of problems and persevere in solving them.
MP2: Reason abstractly and quantitatively
MP3: Construct viable arguments and critique the reasoning of others
MP4: Model with mathematics
MP5: Use appropriate tools strategically
MP6: Attend to precision
MP7: Look for and make sense of Structure
MP8: Look for and express regularity in repeated reasoning.
You may also wish to review the full set of Common Core State Standards in Math and/or videos of the Math Practices enacted in Investigations.
This chart was created by Bill McCallum in an attempt to provide some higher order structure to the practice standards, just as the clusters and domains provide higher order structure to the content standards.
MATH STANDARDS
| Grade | CCSS Content Standards Multiplication and Division |
|---|---|
| 2 | 2.OA.4 Use addition to find the total number of objects arranged in rectangular arrays with up to 5 rows and up to 5 columns; write an equation to express the total as a sum of equal addends. |
| 3 | 3.OA.1 Interpret products of whole numbers, e.g., interpret 5 × 7 as the total number of objects in 5 groups of 7 objects each. For example, describe a context in which a total number of objects can be expressed as 5 × 7. 3.OA.2 Interpret whole-number quotients of whole numbers, e.g., interpret 56 ÷ 8 as the number of objects in each share when 56 objects are partitioned equally into 8 shares, or as a number of shares when 56 objects are partitioned into equal shares of 8 objects each. For example, describe a context in which a number of shares or a number of groups can be expressed as 56 ÷ 8. 3.OA.3 Use multiplication and division within 100 to solve word problems in situations involving equal groups, arrays, and measurement quantities, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem.1 3.OA.4 Determine the unknown whole number in a multiplication or division equation relating three whole numbers. For example, determine the unknown number that makes 3.NBT.3 Multiply one-digit whole numbers by multiples of 10 in the range 10–90 using strategies based on place value and properties of operations. |
| 4 | 4.NBT.5 Multiply a whole number of up to four digits by a one-digit whole number, and multiply two two-digit numbers, using strategies based on place value and the properties of operations. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models. 4.NBT.6 Find whole-number quotients and remainders with up to four-digit dividends and one-digit divisors, using strategies based on place value, the properties of operations, and/or the relationship between multiplication and division. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models. |
| 5 | 5.NBT.5 Fluently multiply multi-digit whole numbers using the standard algorithm. 5.NBT.6 Find whole-number quotients of whole numbers with up to four-digit dividends and two-digit divisors, using strategies based on place value, the properties of operations, and/or the relationship between multiplication and division. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models. |
Key Learning
- The foundational aspects of computational fluency – accuracy, efficiency and flexibility- develop from Kindergarten to grade 5. At each of those grade levels, what it means to be computationally fluent with one or more of the four operations in the base-ten number system is different (e.g., range of numbers, tools and representations, sophistication of strategies).
- The teacher’s role in supporting students’ development of computational fluency is critical. It’s not the activities that develop fluency, it’s how the teacher uses the opportunities they create to move the students in that direction.
- Starter problems and cluster problems help students develop flexible strategies for whole number computation.
- By making observations and posing well-timed questions, teachers can invite students into the CCSS Math Content Standards and Standards for Mathematical Practice.
Notebook
Fill out the Session 6 Notebook Page to reflect on your own learning and record ideas that you want to remember and/or try with students.
Select the following links to go to the Notebook.