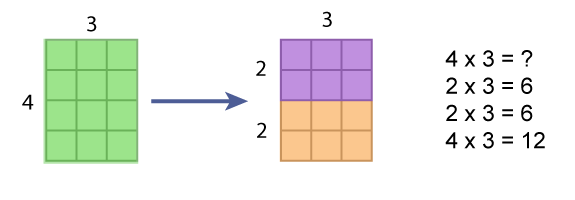
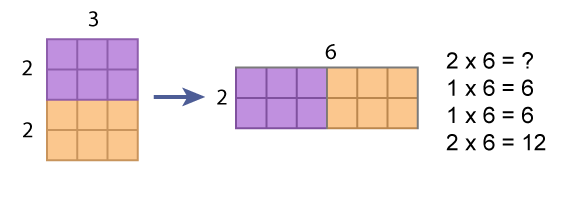
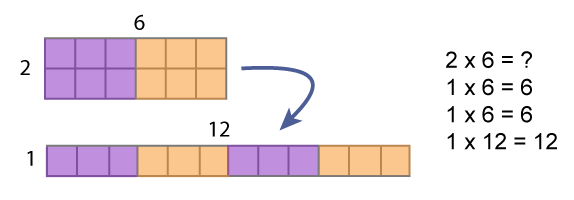
Overview
Session Summary
In this session you will have an opportunity to both solve multiplication problems yourself and examine how children make sense of the operation of multiplication and develop strategies for solving multiplication problems. You will engage in mental math, examine an area model of multiplication, write story contexts and view video clips of students working to develop strategies for multiplication.
The Common Core Standards set expectations for students to have both a solid understanding of multiplication situations, and several efficient strategies for solving problems by the end of fifth grade. You will consider how students build understanding of number and operations, and how this understanding leads to strategies for solving multiplication problems. Students formally study the U.S. Standard Algorithm for multiplication in grade 5.
Before you begin to look how students think about multiplication in the upper grades, consider the foundations they bring from their work with number in the lower grades. What mathematical ideas and experiences prepare young children for multiplication?
Think about what mathematical ideas and experiences prepare young children for multiplication.
Session Focus
In this session you will:
- Consider what students need to know in order to be able to multiply
- Understand and apply properties of operations as strategies to solve multiplication problems
- Consider contexts and representations that support understanding the meaning of multiplication (e.g., array and unmarked array model)
- Examine strategies that students use to solve multiplication problems
- Consider how students develop computational fluency for multiplying whole numbers
Getting Started: Equal Groups
Quick Images: Dot Image
In this activity you will use the quick images to think about the connection between these visual images and the operation of multiplication. The dot images you will be looking at are organized in equal groups of rows and columns. These arrangements can encourage students to think about equal size groups.
Record multiplication expressions that represent this dot image.

Click the show link to view multiplication expressions for this dot image. Check to see how each expression can be represented in the image.
3 x 3 x 2
9 x 2
3 x 6
3 x 2 x 3
Record multiplication expressions that represent this dot image.

Click the show link to view multiplication expressions for this dot image. Check to see how each expression can be represented in the image.
8 x 7 =
(8 x 6) + (8 x 1)
2 x (4 x 7)
(7 x 4) + (7 x 4)
(12 x 4) + (2 x 4)
Notebook
Reflect on the following prompts in your notebook.
- How would you define multiplication?
- How do experiences such as skip counting encourage multiplicative thinking?
- In what ways are multiplication and addition the same? How are they different?
Readings
Images of Multiplication, from Factors, Equal Groups (Grade 3)
Representing Multiplication with the Number Line, from Equal Groups (Grade 3)
Representing Multiplication with Arrays, from Equal Groups (Grade 3)
Finding the Number of Squares in an Array, from Equal Groups (Grade 3)
Visualizing Arrays, from Multiple Towers and Division Stories (Grade 4)
Multiplying by Multiples of 10 from Multiple Towers and Division Stories (Grade 4)
Solving 17 x 6, from Multiple Towers and Division Stories (Grade 4)
Multiplication Strategies, from How Many Packages? How Many Groups? (Grade 5)
How Did You Finish the Problem?, from How Many Packages? How Many Groups? (Grade 4)
Naming Multiplication Strategies, from Number Puzzles and Multiple Towers (Grade 5)
Multiplying with More Than Two Numbers from Number Puzzles and Multiple Towers (Grade 5)
The readings above are all published in Russell, S.J.; Economopoulos, K.; Wittenberg, L.; et al. Investigations in Number, Data, and Space®, Second Edition. Glenview: Pearson, 2012.
Activity 1: Arrays
In this activity, you will consider how students make use of arrays as they become fluent with multiplication combinations, and examine an 8 by 6 array and use it as a focus for a discussion of the array model.
Arrays
An array is a way to represent multiplication using an area model. You are going to be working with arrays that show each individual square unit and with unmarked arrays, which do not use a grid of units. Each side of an array or each dimension of an array represents one factor and the total area represents the product. Students decompose only one of the dimensions at a time.
Slideshow
Developing Fluency with Multiplication Combinations
In third grade, students begin working on developing fluency with multiplication combinations. One of the ways that students build fluency is by making connections among the different combinations. They begin to recognize how smaller combinations can be put together to make larger combinations.
Using multiplication combinations you know
When students learn multiplication combinations, they begin with known multiplication combinations (facts they can use easily) to determine the product of more difficult combinations.
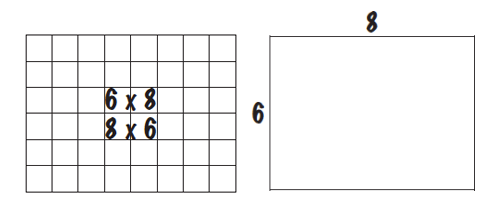
Make a list of multiplication combinations that might help students solve 8 x 6.
Use the 6 x 8 Array PDF to represent three ways 6 x 8 can be solved decomposing one factor at a time.
Example: The arrays below show how knowing 3 x 8 is useful for finding the solution to 6 x 8. Note that in the new array there are two arrays of the same dimension so we only need to compute 3 x 8 once and combine the partial products.
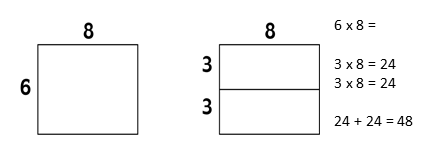
Click show to review other ways that students decompose the factor 6.
8 x 6 (decomposing the factor 6)
8 x 3 and 8 x 3 (the same combination twice)
8 x 5 and 8 x 1 (students learn their fives quickly)
8 x 2 and 8 x 2 and 8 x 2 (16 tripled)
8 x 4 and 8 x 2 (if you know 8 x 2 you can double that answer and add)
Click show to review other ways students decompose the factor 8.
8 x 6 (decomposing the factor 8)
6 x 4 and 6 x 4 (the same combination twice)
6 x 5 and 6 x 3 (students learn their fives quickly)
6 x 6 and 6 x 2 (students learn their doubles and square numbers quickly)
Click show to review other ways students extend the array 6 x 8.
Extending the Array
Students may extend the array to an 8 x 8 and then subtract 16.
Some students may extend the array and subtract 2 squares instead of 16 (2 groups of 8).
Activity 2: Mental Math
In this activity you will solve two multiplication problems using different strategies. You will make a representation with an array and connect a story context to the array and examine strategies to identify the decomposing moves that occur implicitly.
29 x 4
- Mentally solve the problem.
- Jot down your steps in your notebook after you have solved the problem.
- Represent the strategy using an unmarked array.
Strategy Sorting Activity
In this sorting activity, match the equation with the appropriate unmarked array.
Represent the strategy using an unmarked array.
Note: Each of the array representations you sorted is based on the distributive property. As students represent multiplication with arrays they develop strategies for breaking numbers apart and a mental model of how those parts combine to find the final product. When students decompose the factors, find and add all the partial products they are using the distributive property. Partial products are revealed in each of the arrays.
Partial products are revealed in each of the arrays.
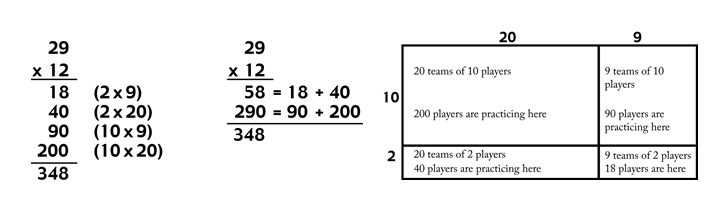
For example, 29 x 4 = (20 x 4) + (9 x 4)
The partial products are (20 x 4) and (9 x 4).
29 x 12
- Estimate the product.
- Solve the problem.
- Jot down your steps in your notebook.
- Write a story for the problem 29 x 12.
- Represent your strategy using an unmarked array indicating how it connects to your story.
Context Sorting Activity
In this sorting activity, match the story to the equation and array.
You examined different strategies for solving multiplication problems. As you solved these problems, you paid attention to how you decomposed the numbers you worked with so that you could operate in ways that were convenient and efficient.
Students in grade five spend time analyzing the U.S. Standard Algorithm and comparing it to their own strategies. Notice the connection between the array model and partial products and the U.S. Standard Algorithm. There are four partial products when both factors are decomposed -the distributive property is being applied twice.
Note: Adding a Zero
Many students say that, to multiply by a multiple of 10, they can ignore the zero, multiply the other digits, and then “add the zero” to get the answer. For example, to find 5 x 30, they can calculate 5 x 3 = 15, then “add a zero” to 15 to find the answer 150.
To ensure students understand the procedures they are using, some teachers react to such statements literally. For example, “Keith told me to add a zero. So 15 + 0. Wait a minute. Does 15 + 0 = 150?”
This “adding a zero” strategy is based on the associative property of multiplication.
In this case, 5 x 30 = 5 x (3 x 10) = (5 x 3) x 10 = 15 x 10.
Activity 3: Observing Students at Work
In this activity you will examine the strategies students typically use as they solve multiplication problems. You will watch video clips of third and fifth grade students solving multiplication problems. After each set of clips, you will reflect on questions that focus on how these students are making sense of multiplication and the number relationships that they use in their strategies.
Read
Read Multiplication Strategies.
Notebook
Take notes in your Notebook as you view each student. Look for similarities in these students’ strategies to the ones you were using to solve the mental math problems.
Ryshawn and Nicholas
View the video clips of students solving multiplication problems twice. Watch the complete clip the first time. The second time take notes about the students’ strategies.
Notebook
In your notebook, reflect on the following questions:
- What is similar about Ryshawn and Nicholas’ strategies? What is different?
- How would you apply Nicholas’ method to a number in the hundreds (e.g., 324 x 8)?
- Think of another problem that you could solve Ryshawn’s way. Are there other numbers like 25 that are convenient to use in multiplication?
Click show to review strategies that Ryshawn and Nicholas used.
- Ryshawn and Nicholas both decompose the 29 to multiply easier pieces by 4.
- Ryshawn understands multiplication as repeated addition and uses that knowledge is his computation. Nicholas, by contrast, is comfortable using multiplication notation.
- Nicholas decomposed 29 by place (into 20 + 9), and he would likely do the same for a three-digit number, such as 324 = 300 + 20 + 4.
Jemea
View the video clip of Jemea solving a multiplication problem twice. Watch the complete clip the first time. The second time take notes about Jemea’s strategies.
Use the following context to apply and analyze Jemea’s strategy:
Tennis Tournament Story Problem
There are 12 teams in a tennis tournament.
Each team has 29 players.
How many tennis players are in the tournament?

Jemea changed the problem from 29 x 12 to 30 x 12. Using the tennis tournament problem above
- how she changed the numbers to make the problem easier
- how she compensated for that change?
Thomas 36 x 17
Thomas’ method for solving 36 x 17 involves changing both numbers in the problem, but does not yield the right answer. Thomas may appear to be put on the spot in this video. The classroom culture that the teacher has created is one in which learning from mistakes is valued. Students are familiar with working this way.
Watch Thomas solving a multiplication problem at least two times. View the complete clip the first time. The second time take notes about Thomas’ strategy.
Building the Model
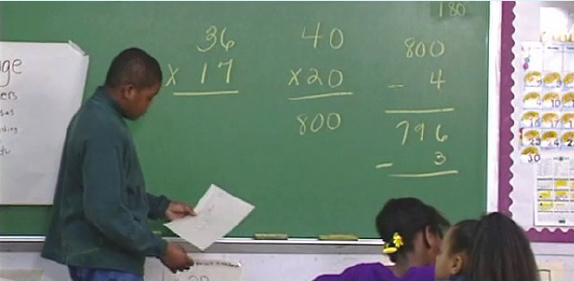

- Construct an array model to represent the action in Thomas’ solution.
- Use your model to show what went wrong with his strategy.
- Use your model and Thomas’ first step (40 x 20) to find the accurate solution for 36 x 17.
Notebook
In your notebook, reflect on the following questions:
- What does Thomas understand about multiplication?
- What does he not yet understand?
Final thoughts…
One aspect of the work that students do when solving computation problems in the four different operations is to see how different operations relate to one another. For example, addition and multiplication are commutative, both addends and factors can be “switched around,” but the same is not true of subtraction or division.
Students often try out strategies that worked in one operation when working on a new operation, as Thomas did in solving 36 x 17. His strategy, if applied to the addition problem 36 + 17, yields the right answer. When we add, we are combining amounts of like things, such as “36 players on one team and 17 players on another team.” If we add too many players, then we can subtract that number later. However, when we multiply, we are counting two different totals: the total amount of groups and the total amount in all the groups. If we change the size of the group and the size of each group, then it is more complicated to make adjustments.
Discussion
How does using strategies based on place value and properties of operations along with arrays, area models and equations help students efficiently solve multiplication problems?
Cite evidence of MP 5 (Use appropriate tools strategically) and MP 7 (Look for and make use of structure).
What multiplication ideas and experiences prepare children in the primary grades for multiplication?
Common Core Alignment
The content in this session is aligned to the following Common Core State Standards and Math Practices:
MATH PRACTICES
MP1: Make sense of problems and persevere in solving them.
MP2: Reason abstractly and quantitatively
MP5: Use appropriate tools strategically
MP6: Attend to precision
MP7: Look for and make use of structure
MP8: Look for and express regularity in repeated reasoning.
You may also wish to review the full set of Common Core State Standards in Math and/or videos of the Math Practices enacted in Investigations.
This chart was created by Bill McCallum in an attempt to provide some higher order structure to the practice standards, just as the clusters and domains provide higher order structure to the content standards.
MATH STANDARDS
Operations and Algebraic Thinking 3.OA
3.OA.1, 2, 3, 4, 5, 6, 7
Represent and solve problems involving multiplication and division.
- Interpret products of whole numbers, e.g., interpret 5 × 7 as the total number of objects in 5 groups of 7 objects each. For example, describe a context in which a total number of objects can be expressed as 5 × 7.
- Multiplication and division within 100 to solve word problems in situations involving equal groups, arrays, and measurement quantities, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem.
- Determine the unknown whole number in a multiplication or division equation relating three whole numbers. For example, determine the unknown number that makes the equation true in each of the equations 8 × ? = 48, 5 = ? ÷ 3, 6 × 6 = ?.
Understand properties of multiplication and the relationship between multiplication and division.
- Apply properties of operations as strategies to multiply and divide. Examples: If 6 × 4 = 24 is known, then 4 × 6 = 24 is also known. (Commutative property of multiplication.) 3 × 5 × 2 can be found by 3 × 5 = 15, then 15 × 2 = 30, or by 5 × 2 = 10, then 3 × 10 = 30. (Associative property of multiplication.) Knowing that 8 × 5 = 40 and 8 × 2 = 16, one can find 8 × 7 as 8 × (5 + 2) = (8 × 5) + (8 × 2) = 40 + 16 = 56. (Distributive property.)
Multiply and divide within 100.
- Fluently multiply and divide within 100, using strategies such as the relationship between multiplication and division (e.g., knowing that 8 × 5 = 40, one knows 40 ÷ 5 = 8) or properties of operations. By the end of Grade 3, know from memory all products of two one-digit numbers.
Number and Operations in Base Ten 3.NBT
3.NBT.3
Use place value understanding and properties of operations to perform multi-digit arithmetic.
- Multiply one-digit whole numbers by multiples of 10 in the range 10–90 (e.g., 9 × 80, 5 × 60) using strategies based on place value and properties of operations.
Number and Operations in Base Ten 4.NBT
4.NBT.3, 5, 6
Generalize place value understanding for multi-digit whole numbers.
- Use place value understanding to round multi-digit whole numbers to any place.
Use place value understanding and properties of operations to perform multi-digit arithmetic.
- Multiply a whole number of up to four digits by a one-digit whole number, and multiply two two-digit numbers, using strategies based on place value and the properties of operations. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.
Key Learning
- Multiplication is about equal-sized groups.
- Students use known multiplication combinations (facts) to determine the product of more difficult combinations.
- Students apply properties of operations to multiplication problems (distributive property, commutative property, associative property).
- When students solve multiplication problems, they most often use strategies that involve breaking numbers apart to create problems that are more manageable and that make use of familiar number relationships.
- Students use representations, models, such as arrays and contexts to help them make sense of and solve multiplication and division problems.
- Students become fluent with multiplication through practice with a variety of contexts and representations that attach meaning to the problems they are solving.
Notebook
Fill out the Session 4 Notebook Page to reflect on your own learning and record ideas that you want to remember and/or try with students.
Select the following links to go to the Notebook.
Please contact ETLO to report any broken links or other problems with this page.