Overview

Session Summary

To be added

Session Focus

In this session you will:

• Apply and extend previous understandings of multiplication to multiply a fraction by a whole number and a fraction by a fraction
• Understand a fraction a/b as a multiple of 1/b (unit fraction)
• Use this understanding (of unit fractions) to multiply a fraction by a whole number or by a fraction using visual models
• Solve word problems involving multiplication of a fraction by a whole number and fraction by a fraction, e.g., by using visual fraction models and equations to represent the problem

Getting Started: Ideas about Fraction Multiplication

Click the show to watch/listen to Investigations author Keith Cochran talking about the work of fraction multiplication.

Skip Counting by Fractions

Students skip count by fractions and use the number line as a visual representation to solve problems involving multiplication of a whole number by a fraction. For example, when they count around the room by 1/3s, they may notice:

• after 3/3 come 4/3, 5/3, ...
• fraction and whole number equivalents: 3/3 = 1, 6/3 = 2, 9/3 = 3, etc.
• whole numbers are fractions: 1 = 3/3, 2 = 6/3
• 4/3 is 4 times the unit fraction 1/3 (4/3 = 4 x 1/3); 7/3 = 7 x 1/3, etc.
• the 4th person will say 4/3 (1/3 x 4 = 4/3); the 7th person, 7/3, etc.
• the fractions they are counting are numbers on the number line

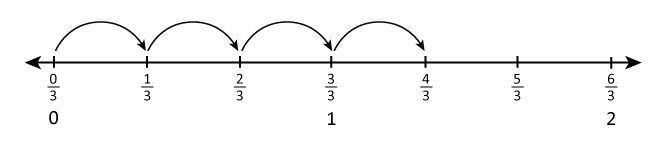
Skip Counting by 4/7

Start to count by 4/7, and place each count on a number line.

• What number will the 5th person say? How do you write that fraction as a mixed number?
• What number will the 14th person say? How do you write that fraction as a whole number?
• What multiplication equation would represent 14 people counting by 4/7?

Activity 1: Fraction Equivalencies

In this activity you will revisit fraction comparison and examine the role of multiplication and division in finding common denominators.

In a previous session, you compared fractions to decide which was larger. You did the comparison using your fraction cards and/or comparing both fractions to a landmark (e.g., 0, 1/2, or 1). You also put fractions in their appropriate containers and watched as students in one classroom determined into which containers to place given fractions. At the end of that lesson a student asked, “Could you make sevenths into another fraction?” The question provided an opportunity to deepen the students’ understanding about equivalent fractions. Later a student asked another question, “Can you use it on any other fractions?” This is the beginning of making a generalization about equivalent fractions. Watch as the teacher facilitates this conversation.

Finding Equivalent Fractions using Halves and Fourths

Finding Equivalent Fractions using Thirds and Sixths

Video

Video to be added

Finding Common Denominators

Equivalent fractions can be created by multiplying both the numerator and denominator by the same number or by dividing a shaded region into various parts. For example, looking at fractions equivalent to 1/2, you can think about the numerator being one-half of the denominator and you can also see it as multiplying 1/2 by 1, where 1 could be 2/2, 3/3, etc. Students’ experiences should focus on visual fraction models rather than algorithms.

Fraction Games - Addition and Subtraction

In this activity you will play three fraction games that give students a context to add and subtract fractions - a model for representing and combining fractions whose denominators are factors of 12. You will examine fraction computation in these games.

Fraction Cookies

Pattern blocks (virtual or real)

Demo: How to Play

Play Subtraction Version

Roll Around the Clock

You will play an addition game called "Roll Around the Clock" which involves another representation, clock fractions. The clock is a useful real world model for adding fractions. It is also important for students to use ideas they have learned earlier when they add fractions. Most students can rely on their knowledge of fraction equivalents and relationships to add fractions with like denominators (3/4 + 1/4) or to add halves and fourths or thirds and sixths without relying on the clock.

Students focus on the rotation rather than the area when they represent fractions on the clock. For example this clock shows a rotation from 12 to 3. That rotation could be represented using the following fractions: 3/12 of the way around the clock, 1/4 of an hour or 15/60 - 15 minutes out of 60 minutes in an hour.

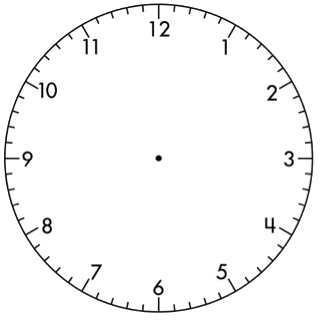
Use the Clock Fractions page from Session 4 Print Materials to record the fraction names and fraction equivalencies (halves, thirds, fourths, sixths, and twelfths) for each of the clocks on the page.

Use the Clock Fractions page from Session 4 Print Materials to record the fraction names and fraction equivalencies (halves, thirds, fourths, sixths, and twelfths) for each of the clocks on the page.

Adding Clock Fractions

Use the clock below to answer the following questions.

If the hand moves one third of the way around the clock, and then it moves one fourth more, what fraction will it have moved altogether? What fractional part of a full rotation is left?

Suppose we added on another half. Where will the clock hand end up? Rotations on the clock can show fractions greater than 1. What fraction names the total turn?

Roll Around the Clock Game

The object of this game is to roll a combination of fractions that add up to 1. For each turn you roll one cube at a time and strategize by deciding which cube to roll and when to stop rolling. The person who rolls closest to 1 gets one point.

Play the game! Click or tap a die to make it roll. If you are on an a mobile device, swipe a die in the direction you want it to spin.

NOTE: A word of caution about using the circle as an area model: Quick and accurate sketches of fractions on a circle are fairly simple to make for halves and fourths, but it can be challenging to partition a circle into equal-size parts for other fractional amounts. Keep in mind that the clock fraction work is intended to be interpreted as a rotation model, not an area model, and that the preprinted clock faces assist us in working with twelfths and their equivalents.

Activity 3

To be added.

Discussion

To be added.

Common Core Alignment

To be added.

Key Learning

To be added.

Notebook

To be added.