Overview
Session Focus
This session focuses on the complexities of making sense of fractions and fraction notation, and the use of representations in Investigations as a part of this process.
Making Sense of Fractions and Fraction Notation
Making sense of fractions and fraction notation is complex. As students move from working only with whole numbers to also working with fractions, they figure out how fractions fit in with what they already know about numbers. As students work with a variety of contexts and representations, they develop an understanding of fractions as equal parts of a whole and as numbers both between and equal to whole numbers. They make sense of fraction notation and the relationship between the numerator and the denominator when they have multiple experiences connecting fraction notation to fraction representations they have created.

Read the blog post Puzzling Through Making Fraction Sets about students puzzling about fractions and fraction notation as they represent unit fractions using an area model.
- What ideas about fractions are students working on making sense of in this blog post?
- What does this blog post highlight about the complexities of fractions?
Materials
Activity 2:
For Fraction Cards
- A pencil or colored pencils
- 20 index cards (4” x 6” preferable) or 20 slips of paper, if index cards are unavailable
- Scissors
- Ruler
- Glue stick
- Fraction Squares (print)
Looking at Student Work Protocol
Activity 3:Activity 1: Representing Fractions Using an Area Model
In this activity you will represent fractions using area models-- a 4 x 6 and a 5 x 12 rectangle-- and consider what students learn about fractions as they represent them on these rectangles.
Developing Meaning for Fractions
Students develop meaning for fractions and fraction notation over time. They work with different models and contexts that enable them to visualize fractions as both equal parts of a whole, and as numbers.
Read the 3rd grade Teacher Note, Developing Meaning for Fractions to learn about the aspects of fractions it is important to make sense of and the ways students work on these ideas in Investigations.
As you read, consider the following questions:
- What key ideas are important for students to make sense of in order to understand fractions?
- What is challenging about developing meaning for fractions and fraction notation?
- How can different fraction models help students makes sense of fractions as both equal parts of a whole and as numbers?
Representing Fractions on Rectangles
Throughout the grades, students use area models to represent fractions as equal parts of a whole. In Investigations students use a variety of area contexts including rugs, flags and brownies. They partition a variety of shapes of different sizes such as circles, rectangles, and pattern block shapes. Representing fractions in a variety of ways supports students in making sense of fractional ideas and developing visual images of fractions.
In fourth grade, students represent fractions on both 4 x 6 and 5 x 12 rectangles.

On 4 x 6 and 5 x 12 Rectangles, represent the following fractions on both a 4 x 6 rectangle and a 5 x 12 rectangle.
| 23 | 26 | 34 |
- How do you know that the amount you shaded in for 26 is 2 6 of the whole?
- How did your understanding of fraction notation help you represent the fractions?
- How is 2 3 of a 4 x 6 and a 5 x 12 rectangle the same and different?
- What do you notice about the relationship between 2 3 and 2 6 after shading in both on the rectangles?
Students represent the same fractions on a rectangle in different ways and then have an opportunity to compare the different ways they represented a fraction.
Click on [show] to see some ways students might represent 3 4 on a 4 x 6 rectangle.
- Did you shade in the rectangle in the same way as one of these?
- How could you prove that the shaded portion on each of the students’ representations shows 3 4?
As students represent fractions using area models and name them using fraction notation, they explore different ways to represent the same fraction, work on what the numerator and denominator represent, compare the same fraction of different size wholes, and notice relationships between fractions.
Activity 2: Representing Fractions Using 2 Different Models
In this activity, you will represent fractions using an area model and a linear model, examine student work on number lines and consider what different understandings students may gain from working with each model.
Using an area model and using a linear model to represent fractions highlight different aspects of fractions. An area model supports students in making sense of fractions as parts of a whole. Representing fractions on a number line supports students in making sense of fractions as numbers and as distances.
Making Fraction Cards
In fourth grade students make fraction cards. Students use the same whole on each card to represent fractions between zero and 2 1/2. Students then use the cards to compare and order fractions.
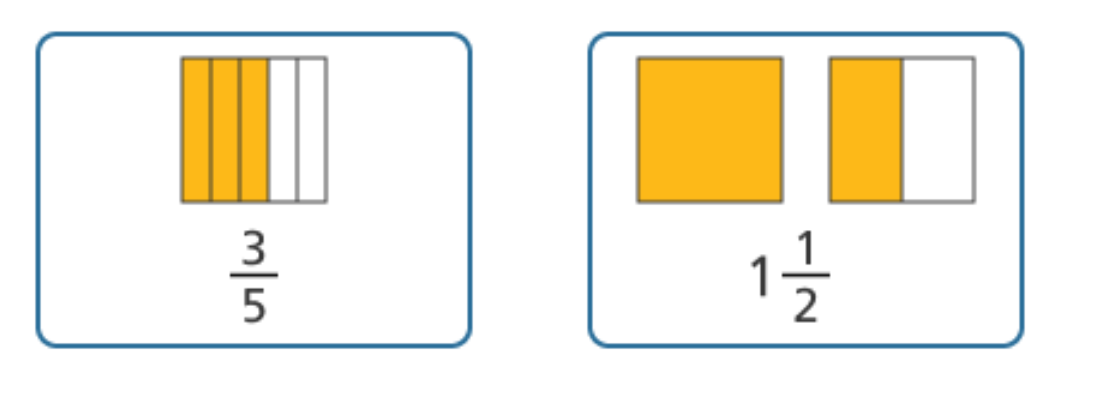
In this activity you will make some fraction cards like those above.
You will need the following materials:
- A pencil or colored pencils
- 20 index cards (4” x 6” preferable) or 20 slips of paper if index cards are unavailable
- Scissors
- Ruler
- Glue stick
- Fraction Squares (print)
Make fraction cards for the following fractions:
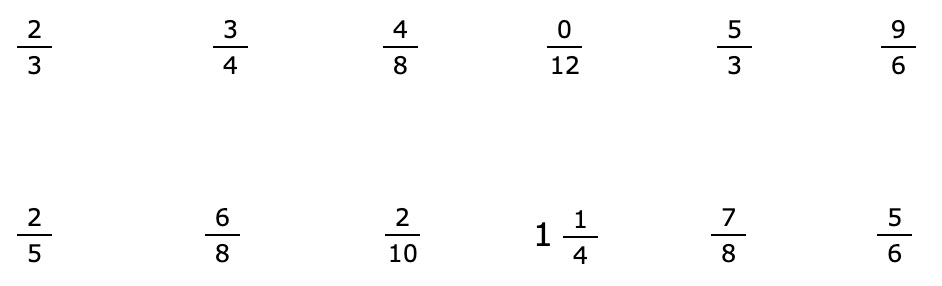
The whole for each of the fraction cards is the square found on the first page of Fraction Squares. Try to draw each fraction as precisely as possible. For some of the fractions you may choose to use the squares already divided into thirds and fifths to help you draw precisely.
For each fraction:
- Cut out a square from one of the pages of Fraction Squares
- Create the fraction by either folding or measuring the square(s) and shading in the appropriate amount
- Position all index cards so the long side of the card is at the top. Glue the square(s) onto the index card
- Label the fraction on the card
In addition, write each of the following landmark numbers on index cards: 0, 12, 1, 2. Save the cards. You will use these cards in Session 3.
Feature - Ongoing Assessment: Observing Students at Work
One feature of the Investigations curriculum found in nearly every session is Ongoing Assessment: Observing Students at Work which includes a set of questions to consider to help teachers focus their observations of students as they do an activity. Use the following Observing Students at Work questions and consider what you might learn about students’ understanding of fractions as they create fraction cards.

NOTE: Students make fraction cards for both fractions greater than one and mixed numbers (e.g., both 96 and 1 14). In Investigations the term “improper fractions” is not used because there is nothing improper about them! Fractional amounts greater than 1 can be represented as either fractions or mixed numbers.
Fractions on a Number Line
In addition to their work with fractions of an area, 3rd grade students also work with fractions on a number line. They are first introduced to fractions on a number line using the context of an ant traveling along city blocks.
Math Words and Ideas
Watch Math Words and Ideas, Fractions on a Number Line to see how students in 3rd grade work with fractions on a number line.
In 3rd grade, students first represent fractions on a 0 to 2 number line and then on a 0 to 3 number line. This highlights the idea that fractions are not just between 0 and 1, but are between (and equal to) whole numbers and that no matter the range of numbers on a number line the location of a fraction is located is always determined by its distance from 0.
Fractions on a Number Line Student Work
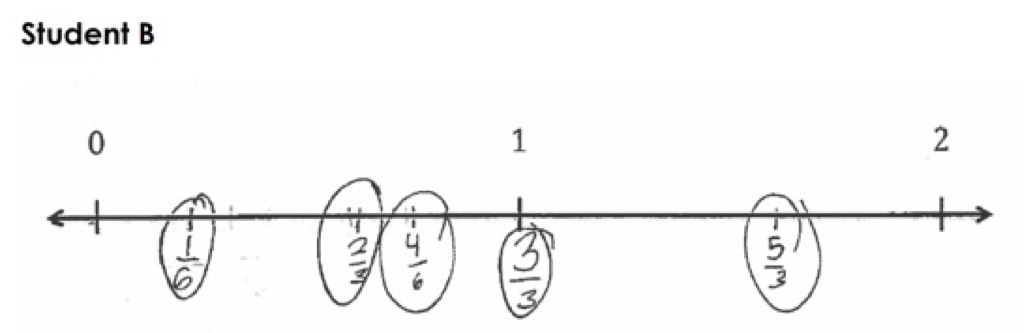
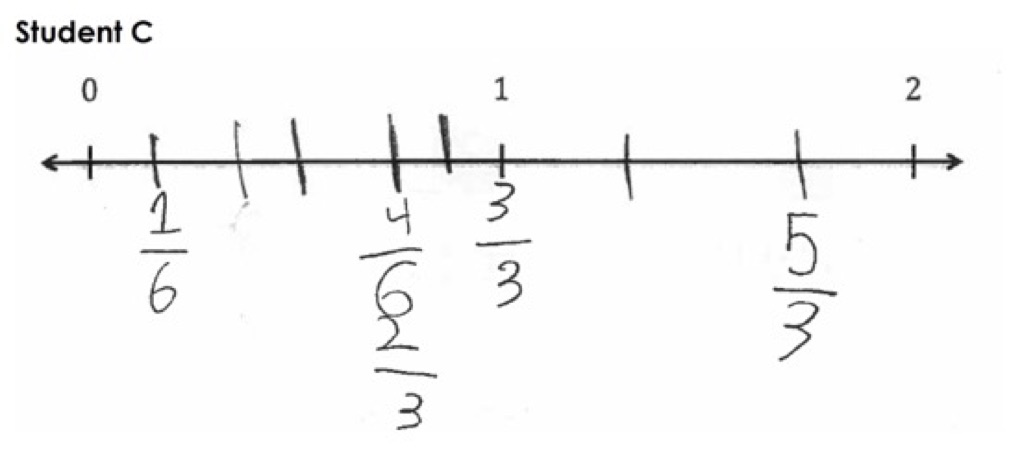
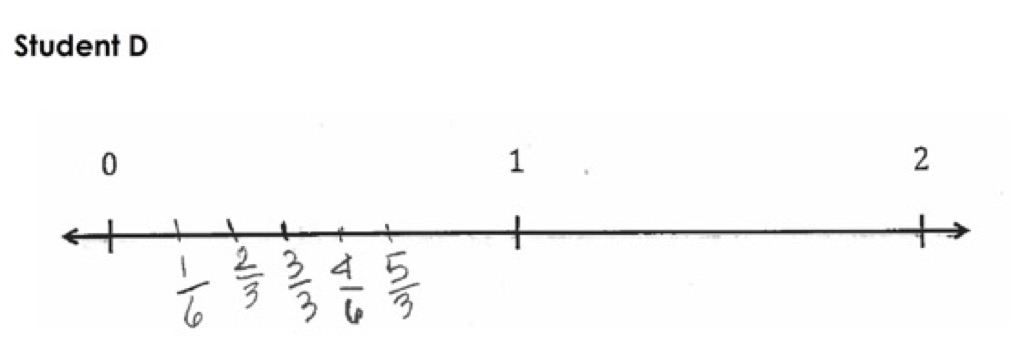
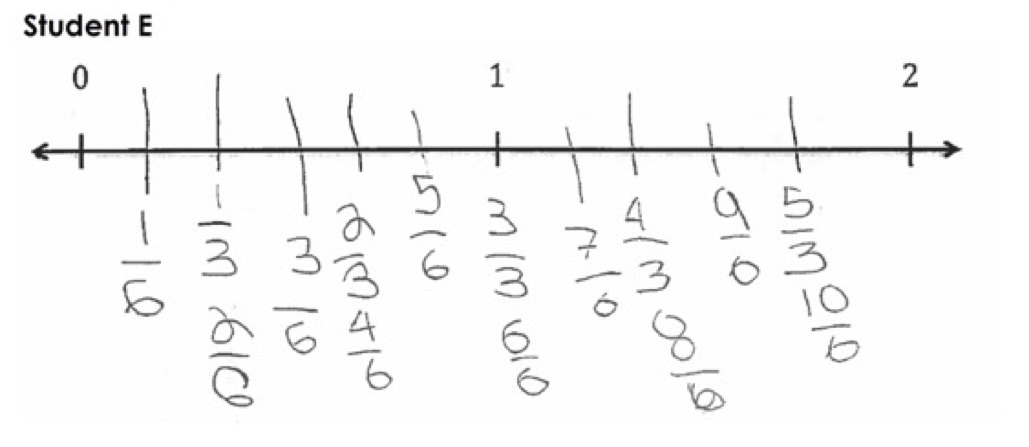
The student work below is from the following 3rd grade assessment:
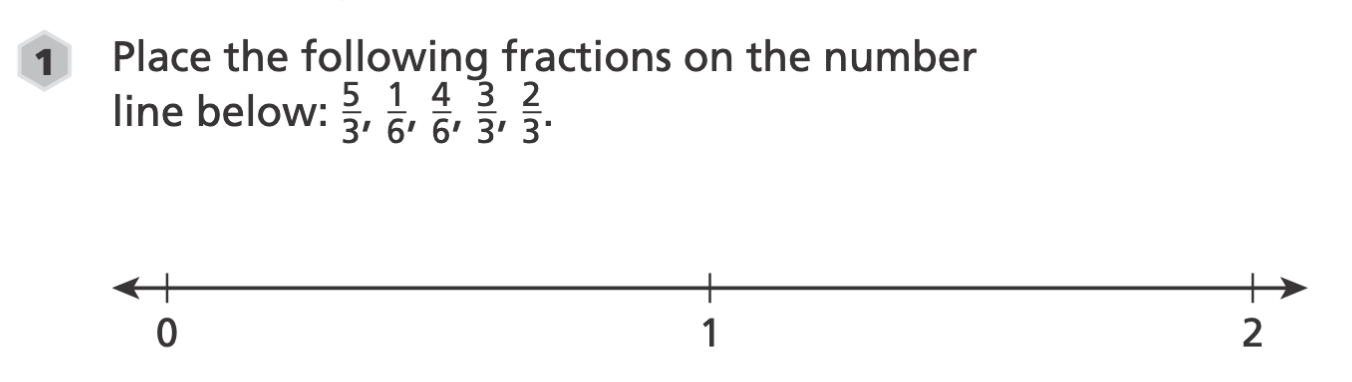
Look at each piece of student work using the LASW protocol.
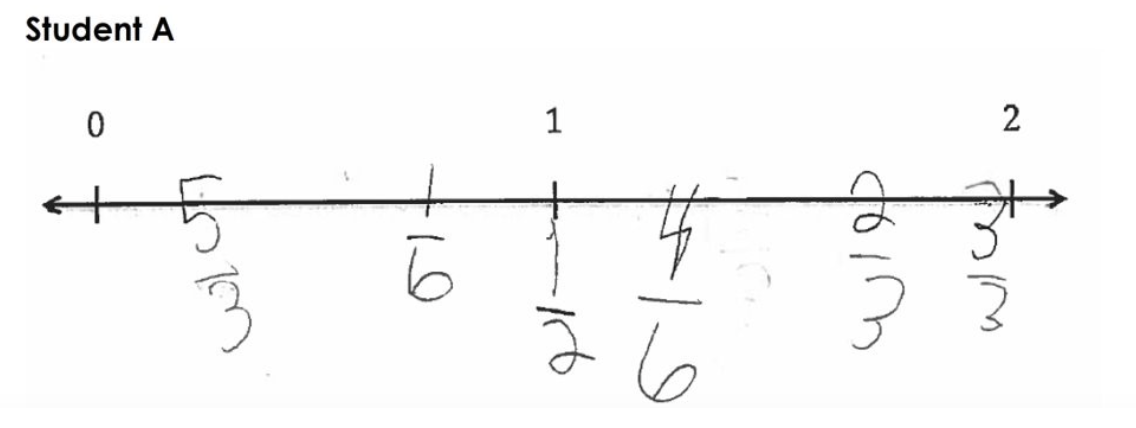
Student A
Student B
Student C
Student D
Student E
Student F
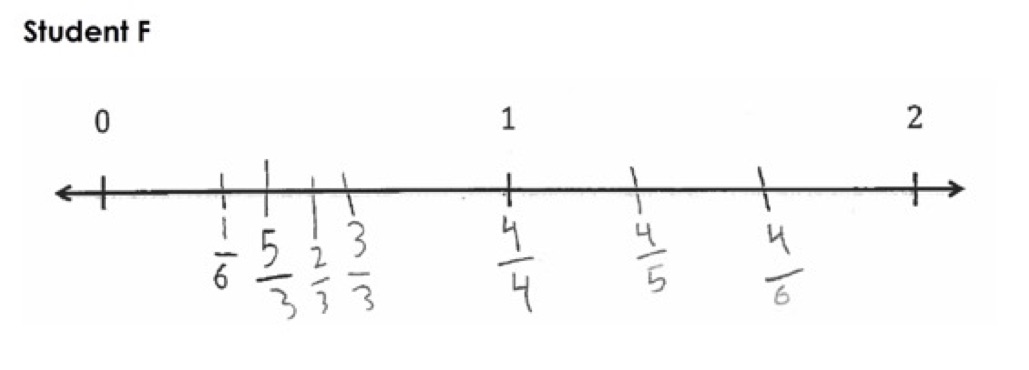
In the Number Line Student Work Forum share your thoughts about one student’s work:
- Describe what the student did in their work.
- Are there any questions you might ask the student to better understand their work?
- What do you think this student understands about fractions?
- What do you think this student is still figuring out about fractions?
Lens on Equity
Teachers have an important impact on students’ mathematical identities through the messages they send about their students’ competencies and abilities.
“The types of feedback that students receive on assessment can contribute to their developing identities as mathematics learners. We encourage more holistic, positive, and specific approaches that give meaningful feedback to students with different levels of understanding. These approaches include focusing students’ attention on making sense of mathematics, affirming evidence of mathematical progress… and providing students with opportunities to grow mathematically without sacrificing their mathematical confidence.” (Aguirre, Mayfield-Ingram, & Martin, 2013, p.68)
In the set of student work above, a number of students did not place all the fractions correctly on the number line.
What feedback might you give some of these students that affirms what they know and are able to do while also helping them move forward in their learning? How do you try to use what your students know to help them move forward?
Consider: What different understandings of fractions might students gain from representing fractions on a number line versus representing fractions with an area model?
Activity 3: Making Sense of Equivalent Fractions
In this activity you will consider how students visualize equivalent fractions as they play a game with pattern blocks and then determine equivalent fractions yourself and justify that they are equal using visual models and reasoning.
Students often notice fraction equivalencies as they use a variety of models to represent fractions. For example, 14 of a 4 x 6 rectangle divided into 2 parts makes 28, and 36 is located at the same point as 12 on a number line. In 3rd and 4th grade, students make lists of equivalent fractions they notice. As students continue to work with fractions, they begin to simply know some fraction equivalencies.
Fraction Cookie Game
In Kindergarten, 1st and 2nd grade, students notice equivalencies among the pattern blocks as they fill in shapes and build shapes. For example, they might notice that 3 green triangles equal 1 red trapezoid. In 3rd grade, students play the Fraction Cookie game where they collect pattern block pieces which they put together to make hexagon “cookies”. One rule of the game is that the players must always have as few pieces as possible at the end of their turn. Therefore, during most turns students need to trade in pieces so that they have the fewest pieces. On a recording sheet they record some of these trades.
Click on the image below to play Fraction Cookie online. If possible, play with a partner. Follow the directions at the top of the game screen. Pay particular attention to steps 4 and 5.

What might students notice about equivalent fractions as they play this game?
Read the 3rd grade Dialogue Box, Playing the Fraction Cookie Game in which a teacher asks some students about the trades they are making during the game.
How are students in the Dialogue Box thinking about equivalent fractions?
Visualizing Fraction Equivalencies
Some people only learn the following rule for determining equivalent fractions—multiply the numerator and the denominator by the same number. In Investigations, students determine equivalent fractions as they work with representations of fractions.
Read Teacher Note from Grade 3 Unit 6, Visualizing Fraction Equivalencies to learn how students use representations to build their knowledge of fraction equivalencies.Consider: How can different visual representations be used to determine and justify equivalent fractions?
Determine an equivalent fraction for each of the following fractions:
| 26 | 34 | 15 | 812 |
- one of the fraction representations explored in this session (4 x 6 or 5 x 12 rectangles, fraction cards, number line, or pattern blocks)
- AND using reasoning with words.
Do NOT use the rule of multiplying the numerator and the denominator by the same number as justification.

Forums
- Once you have completed the work in this session, go to the Session 2 Discussion Forum. Respond to one of the discussion threads in the forum, or start your own thread about a question, idea, or topic of interest that is related to the content of the session.
- After you have posted your comments, take time to read others' posts in the Session Discussion Forum and respond to at least 2 of your colleagues.
- Return to the Number Line Student Work Forum and respond to at least 2 of your colleagues' posts.
Key Learnings
- Representing fractions between 0 and 1 and greater than one using a variety of models helps develop meaning for fractions
- Students use visual models to develop an understanding of fraction notation and interpret the meaning of the numerator and the denominator of a fraction
- Area models help students focus on fractions as equal parts of a whole
- Representing fractions using a number line highlights fractions as numbers and distances
- Students identify equivalent fractions using visual models and justify that they are equivalent
Readings
Hollister, Arusha (2017, October 23). Puzzling Through Making Fraction Sets [Blog post]. https://investigations.terc.edu/puzzling-making-fraction-sets/.
The readings below are all published in Investigations in Number, Data, and Space®, 3rd ed. Northbrook, IL: Savvas Learning Company, LLC, 2017.
- Teacher Note 1: Developing Meaning for Fractions – from Grade 3 Unit 6 Fair Shares and Fractions on Number Lines.
- Dialogue Box 2: Playing the Fraction Cookie Game – from Grade 3 Unit 6 Fair Shares and Fractions on Number Lines.
- Teacher Note 2: Visualizing Fraction Equivalencies – from Grade 3 Unit 6 Fair Shares and Fractions on Number Lines.
