Overview
Session Focus
In this session you will focus on naming and representing fractions, create representations for a given list of fractions, consider the fraction relationship between part and whole when the size of the whole varies, and consider how students connect the meaning of the numerator and the denominator to the representation.
Materials You Will Need for this Session
Pattern Blocks (real or virtual)
Colored pencils
15 index cards (4” x 6” preferable)
Scissors
Ruler
Glue stick
Print the following:
- Crazy Cakes
- Rectangles
- Fraction Squares (print and cut)
There are three types of squares: wholes, thirds and fifths.
Optional Online Resource:
Apps for iPad:
- Virtual Manipulatives! (Fractions, Decimals, Percents)
- Pattern Blocks (Mandalar)
Getting Started: Representing Fractions
Students use a variety of materials to represent fractions across the grades. These representations are important references for students’ understanding of fractions and help students develop mental images of these numbers. They then can call upon these mental images when comparing and computing fractions.
Fraction Representations
Elementary students experience three different fraction representations. Click below to see examples of each.
Example 1: Fractions of an Area

Example 2: Fractions of a Set

Example 3: Fractions on a Number Line

Finding Halves of Crazy Cakes
Students need experiences where they explore fractions that are equivalent but not necessarily congruent. In this activity from Investigations students are given different shaped “crazy cakes” such as the one in Image A and asked to make one cut so two people can share the cake equally. They are asked to justify how they know each piece is the same size.
Example:
One way to cut Crazy Cakes into two equal parts is to cut horizontally so the pieces are a triangle and a square (see Image 2). I can prove the triangle and square pieces are equal. I know if I cut the triangle in half (Image 3) and rotated one of the smaller triangles so the two touch on their diagonal, it would make the square (Images 4 and 5).
Crazy Cake A


Cutting Crazy Cakes
Find a way to cut the cakes in Crazy Cakes so that two people can share each one equally. Remember you can only make one cut.
- How would you cut each cake to show that each person gets exactly half of it?
- Justify your reasoning.
- Post your solutions and justifications on the Sharing Crazy Cakes Solutions Forum. Upload images where appropriate. If you need help uploading an image, you may wish to view a tutorial.
Questions to Consider
Throughout this session, think about the following questions:
- How do models and representations help students focus on the meaning of fractions?
- What makes it challenging for students to interpret the meaning of the numerator and the denominator of a fraction?
- How does working with visual models help students develop an understanding of fraction notation?
- How are the following Math Practices enacted? Cite examples.
- MP5 Use appropriate tools strategically
- MP6 Attend to precision
Readings
Talking About Fraction Flags from Parts of a Whole, Parts of a Group, Gr. 2
Visualizing Fraction Equivalencies from Fraction Cards and Decimal Squares Gr. 4
Dividing Crazy Cakes from Size, Shape and Symmetry Gr. 4
Keeping Track of the Whole from Fraction Cards and Decimal Squares Gr. 4
Are These Equal? from Fraction Cards and Decimal Squares Gr. 4
Visualizing Fractions and Percents from What’s That Portion? Gr. 5
Finding Thirds and Sixths on the Grids from What’s That Portion? Gr. 5
The readings above are all published in Russell, S.J.; Economopoulos, K.; Wittenberg, L.; et al. Investigations in Number, Data, and Space®, Second Edition. Glenview: Pearson, 2012.
Activity 1: Finding Fractional Parts of Rectangles
Overview
In this activity, you will:
- Find fractional parts of rectangular areas
- Interpret the meaning of the numerator and the denominator of a fraction
- Identify equivalent fractions
- Write, read and apply fractional notation
- Compare the same fractional parts of different-sized wholes
In fourth grade, students are expected to extend their understanding of fractional equivalencies. Visual fraction models help them understand how the number and the size of the parts differ, even though two fractions are the same size. For example, 1/2 = 2/4 = 4/8.

Students work with 4 x 6 rectangles.
What fraction of each of these rectangles are shaded?

Consider the following shaded rectangles. How do you know that 1/4 of each is shaded?

Some students' reasons are shown below.
- – They all have six squares
- – I can see that they are each one of four equal pieces
- – I can see that six squares are shaded, and eighteen are not, so 6/18 is shaded.
NOTE: Students come to understand that the number on the bottom of a fraction shows the total number of pieces that make up the whole – the denominator. The number on the top shows how many of those pieces we are talking about – the numerator.
Use the Rectangles recording sheet to shade each of these fractions in a 4” x 6” rectangle and in a 5” x 12” rectangle.
2/3 2/6 2/12
Justify how you know that the region you shaded represents the fractions.
- How are the fractions the same in the different sized rectangles (4 x 6 and 5 x 12)?
- How are they different?
- Is 2/3 of the area of the 5 x 12 rectangle greater than, less than, or equal to (>, <, or =) 2/3 of the area of the 4 x 6 rectangle? How do you know?
Notebook
Record your response to the following questions in your notebook.
- List at least three fractional ideas students use and discover as they solve these problems.
- What do students come to understand when they compare the same fractional parts of different-sized wholes?
NOTE: Same parts, different wholes.
Working with same fractions and different wholes is important because it is at the heart of some complicated ideas of fractions. When represented on a number line, the number 2/3 always has the same relationship to 1 or to other numbers. However, the quantity represented by 2/3 depends on the size of the whole quantity. Two-thirds of a class of 24 students is 16. Whereas two-thirds of the fourth grade – 3 classes, equaling 60 students – is 40. Coordinating these two ideas about fractions and what they represent is complex. Students need time to develop this understanding further as they compare fractional parts.
Activity 2: Creating Fraction Representations
Overview
In this activity, you will:
- Make a Fraction Card set for given fractions including fractions greater than one
- Examine relationships among fractions and fraction equivalences
This work focuses on two ideas:
- 1) understanding that equal fractional parts must be equal sized; and
- 2) knowing that for any whole all the parts combined must equal the whole.
Materials
Colored pencils
20 index cards (4” x 6” preferable)
Scissors
Ruler
Glue stick
Fraction Squares (print and cut out)
Making Fraction Cards
In this activity you will make fraction cards. The whole for the fraction cards is this square. The squares are divided into different parts to help you make the cards: wholes, thirds and fifths.

Make the following fraction cards:

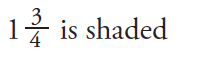
For each fraction:
- Cut the appropriate square(s).
- Create the fraction by either folding or measuring
- Glue the square(s) onto the index card
- Label the fraction
In addition, write each of the following landmark numbers on a separate index card: 0, 1/2, 1, 2.
Save the cards. You will use these cards in Session 3.
Notebook:
As you make the Fraction Cards keep the following questions in mind. Write your reflections in the notebook.
- Which of the fractions are easy to represent and which are more difficult?
- What relationships are you noticing?
- What are you learning about fraction notation?
Fraction Examples

What is the same and what is different about these two cards?
NOTE: Students are expected to quickly and accurately make partitions for halves, fourths and eighths, but to accurately partition the small blank whole squares into thirds or fifths can be challenging and distracting from the mathematical focus of the activity. When students make their cards they can choose from three kinds of wholes available: blank wholes, blank thirds and blank fifths to make their fraction cards. Students may struggle with these ideas at first. For example when students are asked to divide a rectangular area into thirds they sometimes make one of these two errors.
Student A made three unequal sized pieces

Student B cut off part of the whole in order to make the pieces equal; while the three pieces are equal they do not add up to the origianl sized whole.

Students need to have many experiences creating fraction representations in order to support their understanding of fraction concepts and notation.
One Piece is Missing
“A fourth grader was making Fraction Cards for 3/4 and 5/6 and said that she noticed that they both have ‘one piece missing’ so they must be the same size.” Do you agree with that?
Justify your thinking in your notebook.

Note: This idea (the smaller the piece missing, the larger the fraction) is not a rule we want students to memorize. Rather, the idea is connected to the visual representations they have created so that they can reason through this comparison.
Activity 3: Half Yellow
Overview
In this activity you will:
- name and represent fractions on a number line
- identify equivalent fractions
Fractions on a Number line

- Draw a number line
- Label 0 and 2 at each end of the number line
- Starting at 0, mark and label thirds on the number line
- Starting at 0, mark and label sixths on the number line
Look at the fractions on the number line and answer the following questions.
- What do you notice?
- Which if any of the fractions are equal? How do you know?
Imagine two ants are traveling along this number line. Ant A traveled 1/3 the distance from 0 to 2. Ant B traveled 2/3 the distance from 0 to 2.
- Where did each ant stop on the number line?
Imagine ants C and D are traveling along this number line. Ant C traveled 1/3 the distance from 0 to 2. Ant D traveled 1/6 the distance from 0 to 2.
- Where did each ant stop on the number line?
- Which of the four ants traveled the farthest?
The Importance of the Number Line Model
Examining fractions using area representations models is useful. However, reliance on part-whole alone leaves how fractions are related to whole numbers unclear. The number line illustrates fractions as numbers. One of the Common Core standards for third grade students is to understand a fraction as a number on the number line. Using number lines, students learn that:
- Fractions at the same point on the number line are equivalent
- Whole numbers can be represented as fractions
- Fractions are numbers with magnitudes (values) that can be either ordered or considered equivalent
- Fractions provide a unit of measure that allows more precise measurement than whole numbers
- An infinite range of numbers exists between successive whole numbers or between any two fractions
- Two equivalent fractions are the same point on a number line
- Fraction comparison can be notated using symbols >, <, =
Notebook
In the final field of your notebook, reflect on the key take-aways from this session for your own learning and record ideas that you want to remember and/or try with students.
Discussion Forum
- How did making your own fraction cards illuminate for you the meaning of the whole and the parts of a fraction? In what ways will this activity help you assess students’ understandings and misconceptions?
- How does working with visual models help students develop an understanding of fraction notation?
Common Core Alignment
3.NF.A.1 Understand a fraction 1/b as the quantity formed by 1 part when a whole is partitioned into b equal parts; understand a fraction a/b as the quantity formed by a parts of size 1/b.
3.NF.A.2 Understand a fraction as a number on the number line; represent fractions on a number line diagram.
- 3.NF.A.2a Represent a fraction 1/b on a number line diagram by defining the interval from 0 to 1 as the whole and partitioning it into b equal parts. Recognize that each part has size 1/b and that the endpoint of the part based at 0 locates the number 1/b on the number line.
- 3.NF.A.2b Represent a fraction a/b on a number line diagram by marking off a lengths 1/b from 0. Recognize that the resulting interval has size a/b and that its endpoint locates the number a/b on the number line.
3.NF.A.3 Explain equivalence of fractions in special cases, and compare fractions by reasoning about their size.
- 3.NF.A.3a Understand two fractions as equivalent (equal) if they are the same size, or the same point on a number line.
- 3.NF.A.3b Recognize and generate simple equivalent fractions, e.g., 1/2 = 2/4, 4/6 = 2/3. Explain why the fractions are equivalent, e.g., by using a visual fraction model.
- 3.NF.A.3c Express whole numbers as fractions, and recognize fractions that are equivalent to whole numbers. Examples: Express 3 in the form 3 = 3/1; recognize that 6/1 = 6; locate 4/4 and 1 at the same point of a number line diagram.
- 3.NF.A.3d Compare two fractions with the same numerator or the same denominator by reasoning about their size. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with the symbols >, =, or <, and justify the conclusions, e.g., by using a visual fraction model.
4.NF.A.1 Explain why a fraction a/b is equivalent to a fraction (n × a)/(n × b) by using visual fraction models, with attention to how the number and size of the parts differ even though the two fractions themselves are the same size. Use this principle to recognize and generate equivalent fractions.
CCSS Documents
Mathematical Practices Chart
Standards for Mathematical Practice: Commentary and Elaborations for K–5
Key Learning
- Students make meaning of fractions as they name, represent and later compare them.
- Models and representations help students focus on the meaning of fractions as equal parts of a whole.
- Number lines illustrate fractions as numbers.
- Students use visual models to interpret the meaning of the numerator and the denominator of a fraction.
- Students learn that the same parts of different-sized wholes are not the same.
Notebook
Complete the Session 2 Notebook page using the indicated prompts.