Overview
Session Focus
In this session you will apply and extend previous understandings of multiplication to multiply a fraction by a whole number and a fraction by a fraction; understand a fraction as a multiple of a unit fraction and use that understanding to multiply a fraction by a whole number or by a fraction using visual models; and solve story problems involving multiplication of a fraction by a whole number and fraction by a fraction using visual fraction models and equations to represent the problem.
Getting Started: Ideas about Fraction Multiplication
Watch Investigations author Keith Cochran talking about the work of fraction multiplication
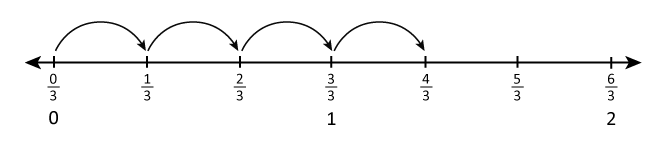
Skip Counting by Fractions
Students skip count by fractions and use the number line as a visual representation to solve problems involving multiplication of a whole number by a fraction. For example, when they count around the room by 1/3s, they may notice:
- after 3/3 come 4/3, 5/3, ...
- fraction and whole number equivalents: 3/3 = 1, 6/3 = 2, 9/3 = 3, etc.
- whole numbers are fractions: 1 = 3/3, 2 = 6/3
- 4/3 is 4 times the unit fraction 1/3 (4/3 = 4 x 1/3); 7/3 = 7 x 1/3, etc.
- the 4th person will say 4/3 (1/3 x 4 = 4/3); the 7th person, 7/3, etc.
- the fractions they are counting are numbers on the number line
Skip Counting by 4/7
Start to count by 4/7, and place each count on a number line.
- What number will the 5th person say? How do you write that fraction as a mixed number?
- What number will the 14th person say? How do you write that fraction as a whole number?
- What multiplication equation would represent 14 people counting by 4/7?
Notebook
Respond to the following questions in your notebook.
- How does using a number line as a visual model and asking questions like the ones you answered for 4/7s contribute to students’ sense making of multiplication of fractions?
Closest Estimate
Another opportunity that allows students to reason about fraction operations is Closest Estimate. Students use mental math as they estimate the closest whole number. This “Number Talk” experience provides students opportunities to discuss their strategies for good estimates and to justify their thinking.
Find the closest estimate for each of the following. Justify your choice for each one.
Notebook
In your notebook, reflect on the following prompts and questions.
- How did you think about each of the numbers?
- How might students make these estimates?
- How are the following Math Practices enacted?
- MP 3 Construct viable arguments and critique the reasoning of others
- MP 8 Look for and express regularity in repeated reasoning
Questions to Consider
Throughout this session, think about the following questions:
- How do contexts and representations help students make sense of multiplying whole numbers by fractions?
- How does using strategies based on properties of operations along with number lines, fraction bars and arrays help students solve fraction multiplication problems?
- How are the following Math Practices enacted? Cite examples
- MP2 Reason abstractly and quantitatively
- MP3 Construct viable arguments and critique the reasoning of others
- MP6 Attend to precision
- MP8 Look for and express regularity in repeated reasoning
Readings
Use of Arrays with Whole Number Multiplication from Factors, Multiples and Arrays and Multiple Towers and Division Stories Gr 4
Using Representations in Brownie Problems: What do you call a third of a half? from Implementation Guide Gr 3
Assessment Finding Fractional Parts and Common Denominator from Fraction Cards and Decimal Squares Gr.4
The readings above are all published in Russell, S.J.; Economopoulos, K.; Wittenberg, L.; et al. Investigations in Number, Data, and Space®, Second Edition. Glenview: Pearson, 2012.
Finding Equivalent Fractions Case
Adapted and reprinted with permission from Connecting Arithmetic to Algebra: Strategies for Building Algebraic Thinking in the Elementary Grades by Susan Jo Russell, Deborah Schifter, and Virginia Bastable. Pp. 30-31. Copyright© 2011 by TERC. Published by Heinemann, Portsmouth, NH. Students’ and teacher’s names are pseudonyms.
Optional Resource / Video
Activity 1: Fraction Equivalencies
In this activity you will revisit fraction comparison and examine the role of multiplication and division in finding common denominators.
In a previous session, you compared fractions to decide which was larger. You did the comparison using your fraction cards and/or comparing both fractions to a landmark (e.g., 0, 1/2, or 1). You also put fractions in their appropriate containers and watched as students in one classroom determined into which containers to place given fractions. At the end of that lesson a student asked, “Could you make sevenths into another fraction?” The question provided an opportunity to deepen the students’ understanding about equivalent fractions. Later a student asked another question, “Can you use it on any other fractions?” This is the beginning of making a generalization about equivalent fractions.
Read Finding Equivalent Fractions by Susan Jo Russell, Deborah Schifter and Virginia Bastable, to see how students in one classroom build on each other’s arguments as they work on a conjecture about the relation between the numerator and the denominator in fractions equivalent to unit fractions.
Notebook
Reflect on the following question in your notebook.
- What did you notice about the teacher’s questions, the use of representations, and how students go from specifics to a more general idea?
Finding Common Denominators
Equivalent fractions can be created by multiplying both the numerator and denominator by the same number or by dividing a shaded region into various parts. For example, looking at fractions equivalent to 1/2, you can think about the numerator being one-half of the denominator and you can also see it as multiplying 1/2 by 1, where 1 could be 2/2, 3/3, etc.
Students’ experiences should focus on visual fraction models rather than algorithms.
Click on the show link to see a set of representations for 1/2 with different denominators.
Click on the show link to see a set of representations for 1/3 with different denominators.
Notebook
Respond to the following question in your notebook.
- How does the work on equivalent fractions lead to an understanding of common denominators?
Activity 2
Overview
In this activity you will multiply a whole number by a fraction, and a fraction by a fraction using fraction bars and arrays as representations. The visual models make the relationship between the denominators of the factors and the denominator of the product explicit.
Note: Students’ Approaches to Solving Fraction Multiplication Problems
The student work and video clips you are about to watch are examples of the ways in which students approach solving fraction multiplication story problems. It is important to ask students to write an equation that matches action in the story. The models and context they use help make the action of fraction multiplication more explicit.
Students often use another operation to solve the problem. For instance, students who solve 120 ÷ 12 may solve this problem using multiplication ideas 12 x 10 = 120 so 12 ÷ 12 must be 10. When students solve fraction multiplication problems they often see division and solve with division. Students’ representations visually lead them to division. In fact fractions themselves have division inherent in the notation 1/12 of 120 is 120/12 which also can be expressed as 120 ÷ 12.
It is important for the teacher to ask questions that focus the students back to the story or problem. When you listen to the video and screencasts in activities 2 and 3, pay attention to the questions the teachers ask to focus students on the meaning of the operation.
Fraction Multiplication: Fraction By Whole Number
Solve each of the following problems. Use a representation to show your thinking.
- Maya runs 1/2 of a mile each day for 12 days. How many miles does Maya run in all?
- K.C. runs 1/4 of a mile each day for 12 days. How many miles does K.C. run in all?
- Joey ran 3/4 of a mile each day for 12 days. How many miles does Joey run in all?
Reflection
For each problem, where in your representation do you see:
- the fraction? fraction of what?
- the whole number?
- the answer?
In what ways might solving the first two problems help with solving the third problem?
Jay’s and Harry’s Representation
Joey ran 3/4 of a mile each day for 12 days. How many miles did Joey run in all?
Look at the following poster created by Jay and Harry.
Reflect on the following questions.
- Where in the representation do you see:
- the fraction? fraction of what?
- the whole number?
- the answer?
- How do they get to the idea that this is a multiplication problem?
Joey’s Run
The students in the following video were given the same three problems you solved. They made posters in preparation for a class discussion of their reasoning. The teacher is facilitating the conversation where students are justifying and making sense of the representation and the solution shared by one pair of students.
Class Discussion about Jay’s and Harry’s Poster
Watch this video twice – first, to understand how the students solved the problem and second, to pay attention to how the teacher probed to illuminate the mathematics.
Making Sense of Isabel's Work
As you watch the next video, reflect on the following questions:
- In what ways did Isabel use the first two problems to help her solve the third problem?
- How did she explain the multiplication ideas?
Notebook Students Sharing: Jay, Harry and Isabel
Respond to the following questions in your notebook.
- What did you notice that the teacher did to promote students’ understanding of fraction multiplication?
- How does the classroom culture help students enact MP3: Construct viable arguments and critique the reasoning of others.
Activity 3
Overview
In this activity you will learn about and experience two representations, fraction bars and arrays, to make meaning of fraction multiplication. You will first multiply whole numbers by fractions and later experience contexts where you will multiply a fraction by a fraction.
Fraction Bars: Multiplying Whole Numbers by Fractions
Fraction bars are used as a representation for fraction multiplication. They are especially useful for multiplying fractions by fractions. To establish and use a fraction bar as a representation, it is helpful to introduce students to fraction bars in a whole number by whole number context first.
Click on the show link to see an example using a bicycle race context.
Emily is in a 50-mile bike race. The fraction bar would look like this.
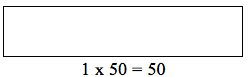
If she ran two such races, the representation would be:
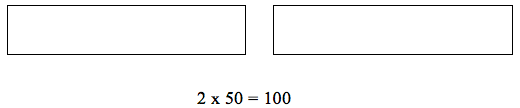
If Emily’s bike broke down, and she only biked half of the 50-mile race, the representation would be:

For the 2 races, the equation is 2 x 50 = 100
For half of the 50-mile race, the equation is 1/2 x 50 = 25
‘1/2 of’ indicates multiplication; just like 2 groups of 50 is multiplication.
Students often use what they know about division to find the solution. They divide the total, 50 miles, into 2 parts, and say that Emily rode 25 miles. They use the fraction bar and divide it into 2 equal pieces, and one of those pieces, because they understand equal shares, would be 25 miles. They may solve it that way, but if you ask them to write an equation that represents the story, the equation is 1/2 x 50 = ?
Bike Race
- Use a fraction bar to represent the following problem.
- Write an equation that represents the story problem.
John is in a bike race. The total distance he bikes is 180 miles. If he biked 1/6 of the distance in one day, how far did he bike?
- What do the three numbers in your equation represent?
- Where do you see 180 and 1/6 in your representation?
- Explain how this is a multiplication problem.
- Where do you see the number of miles he raced in one day in your representation?
Making Sense of Representations, Contexts and Notations
Listen to Investigations author Keith Cochran as he talks about the importance for students to use representations and contexts to make meaning of how fraction multiplication operates.
Students Share Their Thinking
Grace
Watch as Grace shares her solution using the app Explain Everything.
Click on the show link to read the teacher’s reflection on what the student did and next steps.
Grace says she has to divide 180 into 6 pieces. She goes right to using the partial quotients strategy. She clearly understands that 1/6 of 180 means that you are splitting 180 into 6 equal pieces. She never thinks of the problem as 1/6 of 180 or 16/ x 180 even though her class has spent lots of time talking about how finding a fraction of a number can be written as a multiplication problem. She uses an inverse operation but I am not certain that if I gave her this equation 1/6 x 180 = 180 / 6 she would be able to explain if it was true or might even say it isn't true.
Next steps: I would like to see how she would create contexts for the following expressions 1/5 x 60 and 60 x 1/5. Would she create two different contexts? Would the solution paths be different?
Haley
Watch as Haley shares her solution using the app Explain Everything.
Click on the show link to read the teacher’s reflection on what the student did and next steps.
Haley uses the fraction bar model they have used in the Investigations lessons. She begins by showing the whole amount and then attempts to partition the bar into sixths (she does not make equal partitions). She uses 1/2 as a landmark to begin (I loved that!) and then thinks of 90 as being partitioned into 3 parts with each part being 30. I see that work as using a related cluster problem like they do with whole numbers. So I start with 1/2 of 180 or 180/2 then 1/3 of 90 is 30 etc.
Next steps: I wonder if she recognizes that 1/3 of 90 is equal to 1/6 of 180 and why that might be true.
Fraction Bars: Using Arrays to Represent and Solve Fraction Problems
The following screencast shows a fraction bar for multiplying fractions by fractions.
Solve the following problems.
For each problem:
- draw a fraction bar to show your solution
- write an equation
In the problems below, assume one third of each bar is shaded.

- If 1/2 of the shaded part is striped, how much of the bar is striped?
- If 2/3 of the shaded part is striped, how much of the bar is striped?
- Lisa has a bouquet of flowers. A third of the bouquet is roses. Three-fourths of the roses are red. What fraction of the flowers are red roses?
Notebook
Respond to the following questions in your notebook.
- What is happening with the denominators as you multiplied the fractions?
- What do you notice about the denominators of the factors and the denominator of the product?
- Write a generalization that would apply to any product of two fractions
Arrays: Multiplying Whole Numbers
Students use arrays to solve whole number multiplication problems. Arrays can also be used to solve fraction multiplication problems. If this is a new model for you, read Use of Arrays with Whole Number Multiplication to familiarize yourself with how the array models are used for whole number multiplication.
Examples:
Multiplying a Fraction by a Fraction
Watch the following screencast to see how students use the array to solve fraction multiplication problems.
Answer the following questions.
- What fraction of Grandpa’s land does Ed own?
- What fraction of Grandpa’s land did Ed plant with potatoes? How do you know?
- Write an equation that represents this story.
Use an array to solve each of the following problems.
- Cecilia owns 1/3 of a section of land. She plants tomatoes on ½ of her land. What fraction of the entire section is planted with Cecilia’s tomatoes?
- Renaldo owns 1/2 of a section of land. He plants corn on 3/4 of his land. What fraction of the entire section is planted with Renaldo’s corn?
- One wall in Talisha’s bedroom is painted 4/5 green. She put flower stickers on ¾ of the green part of this wall. What fraction of this wall has flower stickers?
- James went to the school fundraiser. He wanted to buy brownies. By the time he reached the table with the brownies, only 2/3 of the pan was left. He bought ¼ of the remaining brownies. What fraction of the original full brownie pan did he buy?
The problems above are adapted from grades 4 and 5 Investigations and the Common Core State Standards © Copyright 2010.
Notebook
In the final field of your notebook, reflect on the key take-aways from this session for your own learning and record ideas that you want to remember and/or try with students.
Discussion
- In what ways do the fraction bars and the arrays illustrate the meaning of fraction multiplication? Cite examples.
- How does the classroom culture help students enact MP3: Construct viable arguments and critique the reasoning of others.
Common Core Alignment
Build fractions from unit fractions.
4.NF.B.4 Apply and extend previous understandings of multiplication to multiply a fraction by a whole number.
-
4.NF.B.4.A Understand a fraction a/b as a multiple of 1/b. For example, use a visual fraction model to represent 5/4 as the product 5 × (1/4), recording the conclusion by the equation 5/4 = 5 × (1/4).
-
4.NF.B.4.B Understand a multiple of a/b as a multiple of 1/b, and use this understanding to multiply a fraction by a whole number. For example, use a visual fraction model to express 3 × (2/5) as 6 × (1/5), recognizing this product as 6/5. (In general, n × (a/b) = (n × a)/b.)
-
4.NF.B.4.C Solve word problems involving multiplication of a fraction by a whole number, e.g., by using visual fraction models and equations to represent the problem. For example, if each person at a party will eat 3/8 of a pound of roast beef, and there will be 5 people at the party, how many pounds of roast beef will be needed? Between what two whole numbers does your answer lie?
Understand decimal notation for fractions, and compare decimal fractions.
4.NF.C.5 Express a fraction with denominator 10 as an equivalent fraction with denominator 100, and use this technique to add two fractions with respective denominators 10 and 100. For example, express 3/10 as 30/100, and add 3/10 + 4/100 = 34/100.
Apply and extend previous understandings of multiplication and division.
5.NF.B.4 Apply and extend previous understandings of multiplication to multiply a fraction or whole number by a fraction.
-
5.NF.B.4.A Interpret the product (a/b) × q as a parts of a partition of q into b equal parts; equivalently, as the result of a sequence of operations a × q ÷ b. For example, use a visual fraction model to show (2/3) × 4 = 8/3, and create a story context for this equation. Do the same with (2/3) × (4/5) = 8/15. (In general, (a/b) × (c/d) = ac/bd.)
-
5.NF.B.4.B Find the area of a rectangle with fractional side lengths by tiling it with unit squares of the appropriate unit fraction side lengths, and show that the area is the same as would be found by multiplying the side lengths. Multiply fractional side lengths to find areas of rectangles, and represent fraction products as rectangular areas.
5.NF.B.5 Interpret multiplication as scaling (resizing), by:
-
5.NF.B.5.A Comparing the size of a product to the size of one factor on the basis of the size of the other factor, without performing the indicated multiplication.
-
5.NF.B.5.B Explaining why multiplying a given number by a fraction greater than 1 results in a product greater than the given number (recognizing multiplication by whole numbers greater than 1 as a familiar case); explaining why multiplying a given number by a fraction less than 1 results in a product smaller than the given number; and relating the principle of fraction equivalence a/b = (n × a)/(n × b) to the effect of multiplying a/b by 1.
6.NF.B.6 Solve real world problems involving multiplication of fractions and mixed numbers, e.g., by using visual fraction models or equations to represent the problem.
CCSS Documents
Mathematical Practices Chart
Standards for Mathematical Practice: Commentary and Elaborations for K–5
CCSS Video from Illustrative Site
Fraction Progression Unit 5 - Multiplication of Fractions, pt.1
Fraction Progression Unit 6 - Multiplication of Fractions pt. 2
Key Learning
- Multiplying a fraction by a whole number is an extension of multiplication of whole numbers
- Understanding a fraction a/b as a multiple of 1/b helps make sense of multiplication of whole numbers by fractions
- Contexts and representations – number lines, rectangles, and arrays – help students make sense of fraction multiplication
- Fraction equivalencies are a result of multiplying by 1, where 1 = a/a, and a is any number, not 0
Notebook
Complete the Session 5 Notebook page using the indicated prompts.