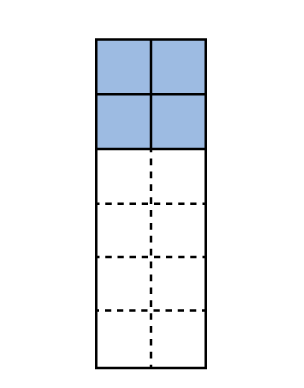
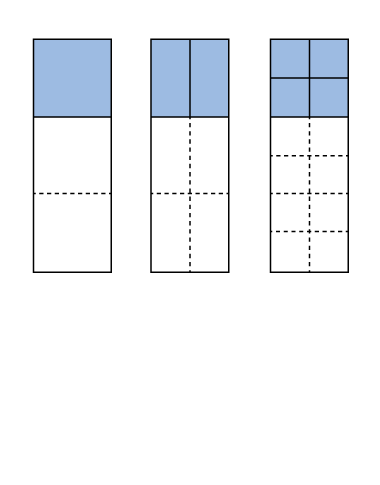
Overview

Sentence above to show you where it is relative to the fractions.

This is a sample fraction in a normal line of text. 1/2 + 3/10 The current limitation is that to be large enough to be this size, the fractions need to be taller than your normal font, so they will bleed into any above lands. To make the fraction fit, it needs to be this size: 1/2 but they may be too small to see.

Session Summary

To be added

Session Focus

In this session you will:

• Apply and extend previous understandings of multiplication to multiply a fraction by a whole number and a fraction by a fraction
• Understand a fraction a/b as a multiple of 1/b (unit fraction)
• Use this understanding (of unit fractions) to multiply a fraction by a whole number or by a fraction using visual models
• Solve word problems involving multiplication of a fraction by a whole number and fraction by a fraction, e.g., by using visual fraction models and equations to represent the problem

Getting Started: Ideas about Fraction Multiplication

Click the show to watch/listen to Investigations author Keith Cochran talking about the work of fraction multiplication.

Skip Counting by Fractions

Students skip count by fractions and use the number line as a visual representation to solve problems involving multiplication of a whole number by a fraction. For example, when they count around the room by 1/3s, they may notice:

• after 3/3 come 4/3, 5/3, ...
• fraction and whole number equivalents: 3/3 = 1, 6/3 = 2, 9/3 = 3, etc.
• whole numbers are fractions: 1 = 3/3, 2 = 6/3
• 4/3 is 4 times the unit fraction 1/3 (4/3 = 4 x 1/3); 7/3 = 7 x 1/3, etc.
• the 4th person will say 4/3 (1/3 x 4 = 4/3); the 7th person, 7/3, etc.
• the fractions they are counting are numbers on the number line

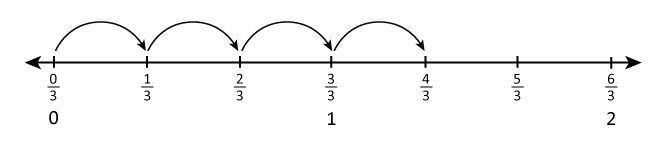
Skip Counting by 4/7

Start to count by 4/7, and place each count on a number line.

• What number will the 5th person say? How do you write that fraction as a mixed number?
• What number will the 14th person say? How do you write that fraction as a whole number?
• What multiplication equation would represent 14 people counting by 4/7?

Readings

To be filled in

Activity 1: Fraction Equivalencies

In this activity you will revisit fraction comparison and examine the role of multiplication and division in finding common denominators.

In a previous session, you compared fractions to decide which was larger. You did the comparison using your fraction cards and/or comparing both fractions to a landmark (e.g., 0, 1/2, or 1). You also put fractions in their appropriate containers and watched as students in one classroom determined into which containers to place given fractions. At the end of that lesson a student asked, “Could you make sevenths into another fraction?” The question provided an opportunity to deepen the students’ understanding about equivalent fractions. Later a student asked another question, “Can you use it on any other fractions?” This is the beginning of making a generalization about equivalent fractions. Watch as the teacher facilitates this conversation.

Finding Equivalent Fractions using Halves and Fourths

Finding Equivalent Fractions using Thirds and Sixths

Video

Video to be added

Finding Common Denominators

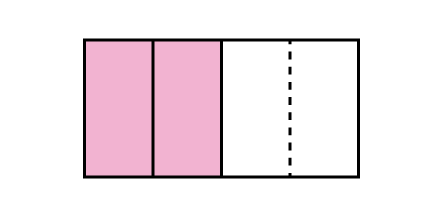
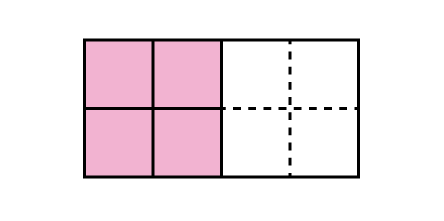
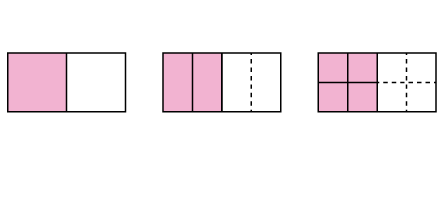
Equivalent fractions can be created by multiplying both the numerator and denominator by the same number or by dividing a shaded region into various parts. For example, looking at fractions equivalent to 1/2, you can think about the numerator being one-half of the denominator and you can also see it as multiplying 1/2 by 1, where 1 could be 2/2, 3/3, etc. Students’ experiences should focus on visual fraction models rather than algorithms.

Activity 2

To be added

Activity 3

To be added.

Discussion

To be added.

Common Core Alignment

To be added.

Key Learning

To be added.

Notebook

To be added.