Overview
Session Focus
In this session you will consider contexts and representations that support understanding the meaning of fractions; see how students’ everyday knowledge of fractions contributes to their fraction work at school, examine ideas and connections students are making as they work with fractions, and work with unit fractions.
Materials You Will Need for this Session
Scissors
Color pencils or markers
Handouts to print
Optional Online Resources
Apps for iPad:
- Virtual Manipulatives! (Fractions, Decimals, Percents)
- Pattern Blocks (Mandalar)
Getting Started: Young Students’ Ideas about Fractions
Students enter school with their own fraction ideas. You will hear them say things like, “I got the smaller half” or, “I have the big half.” Watch and listen as young students share their ideas about a half.
Early Fraction Experiences
Most students enter Kindergarten with ideas about fractions. Their ideas are grounded in personal experiences. They know what it means to share half a sandwich, half their toys, etc. In Kindergarten, they explore ways to build one shape with other shapes (e.g., a hexagon pattern block can be created with two trapezoid pattern blocks). The CCSS list fractions as a standard starting in first grade.
In this session you will read about and experience how first and second grade students explore the following ideas:
- Fractions are equal parts of a whole
- Fractions of a set
- Fraction terms and notation
NOTE: By fraction terms and notation for first and second grade, we mean reading and writing fractions such as 1/2 and 2/3, not learning terms such as “numerator” and “denominator.” Although teachers may use the terms, students are not expected to use these terms at this stage.
Readings
Learning About Fractions from Parts of a Whole, Parts of a Group, Gr. 2
End–of–Unit Assessment from Parts of a Whole, Parts of a Group, Gr. 2
What is One Half? from Parts of a Whole, Parts of a Group, Gr. 2
Fourths: Same or Different? from Parts of a Whole, Parts of a Group, Gr. 2
The readings above are all published in Russell, S.J.; Economopoulos, K.; Wittenberg, L.; et al. Investigations in Number, Data, and Space®, Second Edition. Glenview: Pearson, 2012.
Activity 1: Fold and Fold Again
Overview
In this activity, you will:
- experience an activity called Fold and Fold Again
- focus on an area model for fractions
- prove equivalences among different shaped fourths
Materials
Two More Fourths
Scissors
Markers
Fold and Fold Again is a second grade activity from Investigations. You will use paper squares as one whole.
Fold one square in half using one straight line (fold). To make your fold more visible, trace over the fold line with a marker. Think of two other ways to fold the remaining two pieces of paper in half with one straight line. Make sure you have three different ways.
A horizontal fold and vertical fold are considered one way since they are congruent.
View the following screencast to see different ways students might fold their paper squares.
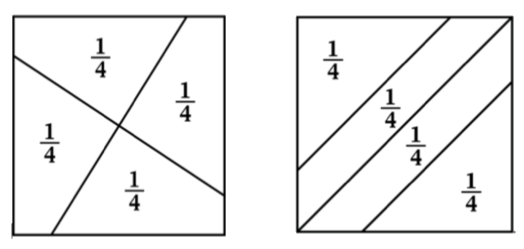
You are going to do the same thing using the following fourths. Using the fourths in Two More Fourths:
- Determine whether each of the two squares is separated into four equal parts.
- Prove that each segment of the whole is equivalent. You may want to use scissors.
Notebook
Respond to the following questions in your notebook.
- Justify how you know if each of the four parts in the square are equal.
- What understandings about fourths are young students developing with experiences such as the Fold and Fold Again activity?
Note
Not all first and second graders will come to agreement about the equivalence of the different shaped fourths. For example, using the context of sandwiches, some students may see some of the pieces as “bigger” than others. This idea may be new to many students and they will revisit this idea in later grades.
Activity 2: Naming Fractional Amounts
Overview
In this activity, you will:
- Use pattern blocks to work on fraction names and relationships among pattern blocks always in relation to a whole
- Use visualization to make sense of fractions and equivalence, working with halves, fourths, sixths, and twelfths
Materials
Pattern Blocks (real or virtual)
Print Materials
Optional Online Resources:
Apps for iPad:
- Virtual Manipulatives! (Fractions, Decimals, Percents)
- Pattern Blocks (Mandalar)
Determining Unit Fractions
Young students use pattern blocks to explore fraction names and relationships before using them as a tool to explore fractional ideas explicitly. They fill in puzzles and build designs with different pattern blocks. They often use fractional ideas and language to describe their work.
It is likely that you have worked with pattern blocks in the context of fraction work where the hexagon is identified as the whole and students are asked to find the fractional value of the other pattern blocks shapes. In this activity you are going to use the following design as one whole.

Fractions with Pattern Blocks
For this part of the activity, you will need pattern blocks and the Naming Fractional Amounts Chart to record your answers to the following questions.
- What fractional part of the whole does each of these pieces represent?
- How do you know?
Using Unit Fractions
Each of the pattern block fractions 1/2, 1/4, 1/16, and 1/12 are unit fractions because the numerators are all equal to one. Students start by naming unit fractions to help them see the part-whole relationship and how those relationships are expressed in fraction notation and in spoken language. They use their knowledge of unit fractions to name fractions that involve more than one part of a whole.
- How would you name the fractional amount covered by the trapezoids?
- How could this amount be recorded?
Equivalent Fractional Amounts
Use pattern blocks to make and record the fractions listed on the Equivalent Fractional Amounts Chart.
Notebook
Record your responses to the following question in your notebook.
- What relationships did you notice as you named the fractions in the Equivalent Fractional Amounts Chart?
View the video below to see an example of how one student filled in 1/4 and justified his reasoning.
Click the show link to see examples of relationships that students have noticed.
“All the ways to make 1 have the same number in the numerator as the denominator.”
“When I made 2/6 I used twice as many twelfths as sixths.”
“The top number in the fraction is the same as the number of pattern blocks.”
“I could’t make fourths using just sixths.”
NOTE
Visualizing fraction equivalencies gives students mental images to draw upon when they are working with fractions and answering questions such as “Which is larger, 3/4 or 5/6?” or adding fractions such as 1 1/2 + 3/4, which are ideas you’ll come back to in upcoming sessions (Comparing Fractions and Adding and Subtracting Fractions).
Activity 3: Half Yellow
Overview
In this activity you will:
- Create a design and consider how the size of a fractional part is determined by its relationship to the whole
- Determine whether half of the area of a pattern block design is yellow
One Third Green Discussion
Melissa and Andrew were building pattern block designs. Andrew made the following design and shared, “I made a hexagon with three pattern blocks. One-third of the pattern block design is green.” Melissa said, “I think your design is one-sixth green.” They continued to discuss and justify their thinking.
Notebook
Respond to the following questions in your notebook.
- Why does Andrew think his design is one third green? What might he have said to justify his thinking?
- Why does Melissa think Andrew’s design is one sixth green? What might she have said to justify her thinking?
Half Yellow
Students use pattern blocks in the primary grades to explore geometric relationships. For example, they learn that two trapezoids equal one hexagon in the set of pattern block shapes. In later grades, they connect their early geometric experiences to their study of fractions concepts, equivalencies and operations.
It is likely that you are familiar with pattern block fractions when one hexagon equals one whole. If the hexagon is the whole then the trapezoid is equivalent to 1/2, the blue rhombus is equivalent to 1/3, and the triangle is equivalent to 1/6.
In other pattern block activities, such as the following activity, the whole is not determined by the yellow hexagon. These types of activities help students pay attention to the whole.
The following activity engages students in creating designs where they make a portion of the design a designated fraction. For this experience, the task is to build a design that is half yellow.
Material
Pattern Blocks (real or virtual)
Pattern Block Design
Determine if the design below is half yellow.
You may want to use pattern blocks to justify your thinking.
Note: Common Misconception
Students may mistakenly say that this design is 2/7 yellow because two out of 7 pieces are yellow. Or they may mistakenly say that this design is 1/3 yellow because yellow is one out of three colors used in the design. In the earlier discussion about 1/3 green, Andrew might have thought his design was 1/3 green because there were three pieces or possibly because there were three different colors. It is important for students to have conversations with others and for teachers to listen to student conversations about the fractional parts of their designs as they make sense of the fractional relationships of the whole design.
One Third Yellow Pattern Block Design
- Make a one third yellow design using pattern blocks.
- You will share your design in this week's Discussion Forum.
Read the following case of Mary and Tamara, Shifting understanding from one third of a discrete whole to one third of a group.
Note: This activity provides an opportunity for students to engage in discussions in which they justify how the size of a fractional part in their design (e.g., yellow hexagons), is determined by its relationship to the whole design; in other words, half of one design can be two hexagons and half of another different-sized design can be three hexagons or more.
Notebook
In the final field of your notebook, reflect on the key take-aways from this session for your own learning and record ideas that you want to remember and/or try with students.
Discussion Forum
- Share your one third yellow design by uploading a picture or screen shot of your design. You may wish to view a tutorial to help you with this part.
- Prove that your design is in fact one third half yellow.
- How might activities like the ones you experienced in this session help students like Andrew understand the importance of the relationship between fractional amounts and the whole?
Remember to post early and return to the discussion forum throughout the week to read and respond to others’ posts.
Common Core Alignment
K.G.B.6 Compose simple shapes to form larger shapes. For example, “Can you join these two triangles with full sides touching to make a rectangle?”
1.G.A.3 Partition circles and rectangles into two and four equal shares, describe the shares using the words halves, fourths, and quarters, and use the phrases half of, fourth of, and quarter of. Describe the whole as two of, or four of the shares. Understand for these examples that decomposing into more equal shares creates smaller shares.
2.G.A.3 Partition circles and rectangles into two, three, or four equal shares, describe the shares using the words halves, thirds, half of, a third of, etc., and describe the whole as two halves, three thirds, four fourths. Recognize that equal shares of identical wholes need not have the same shape.
CCSS Documents
Mathematical Practices Chart
Standards for Mathematical Practice: Commentary and Elaborations for K–5
Key Learning
- Young students develop understandings and ideas about representing fractions through geometry, measurement and real-world experiences.
- Ideas about fractions include unit fractions (e.g. 1/2) and non-unit fractions, such as fractions with numerators greater than 1 (e.g. 3/4).
- Fractional parts are determined by their relationship to the whole.
Notebook
Complete the Session 1 Notebook page using the indicated prompts.