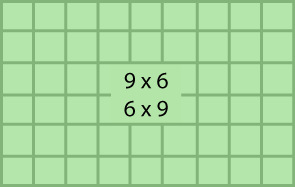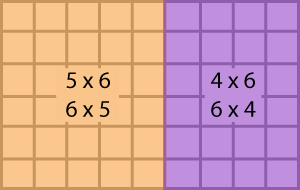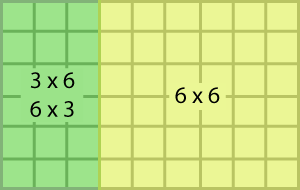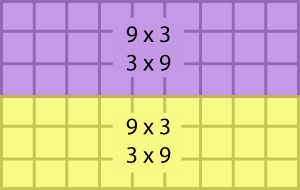This session focuses on the operations of multiplication and division, and the ways in which Investigations supports students in developing an understanding of these operations, the relationship between them and fluency with them.

In this session you will:

• look at various contexts and models students use to make sense of multiplicative relationships and solve multiplication and division problems
• solve some multiplication and division problems, and consider the different strategies students use to solve them
• play multiplication and division games that involve arrays
• learn about activities in Investigations that support students in developing fluency with multiplication facts and efficient problem-solving strategies

Materials

• pennies (12)
• connecting cubes (optional)
• grid paper

Getting Started: Estimating and Solving Multiplication Problems

In this activity, you will mentally solve two multiplication problems and think about how you used your knowledge about the numbers, place value, and the operation of multiplication.

Click on each problem to complete the activity.

Consider:

• What did you understand about multiplication, the numbers, and place value to estimate and later solve the two problems?
• How did estimating the solution first help you solve the problem?

In this activity, you will look at activities from Investigations that support students in building an understanding of multiplication and division through the use of contexts and representations; consider the early strategies students use to solve multiplication problems; and think about the relationship between multiplication and division.

Modeling Equal Groups

Counting by equal groups helps lay the foundation for the work students do in third grade and beyond as they build their understanding of the operations of multiplication and division. Second grade students make a shift from working with and counting by ones to working with and counting by groups.

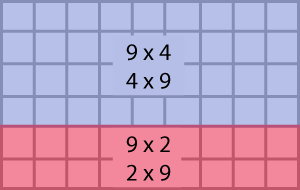
Arrays

An array is an arrangement of objects in equal rows and columns that form a rectangle. Students begin working with arrays in second grade both within a geometry context, when they examine the properties of rectangles that they construct using color tiles, and in the foundations of multiplication unit when they make Cube Buildings.

Solving a “Cube Building” Problem

Students use connecting cubes to create arrays that represent cube buildings. Each cube represents one room, and each floor must have the same number of rooms as the floor below it.

Use the image of the cube building below to solve the following problem. You might want to use connecting cubes to model the problem. Record how you solved the problem.

Think about how you solved this problem. Write an addition equation that represents the total number of rooms in the 10-floor building.

Read Equal Groups: Arrays and Multiplication which discusses how students might solve cube building problems.

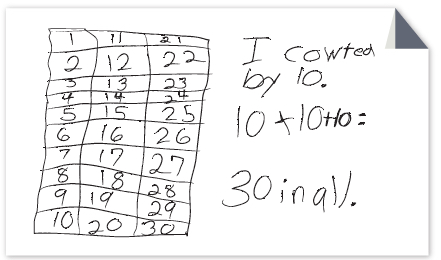
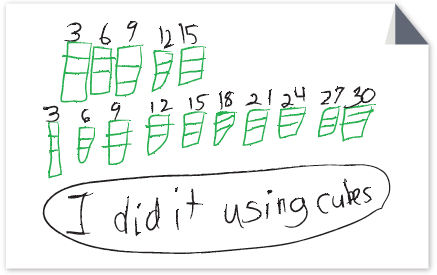
Look at the following student work samples to see how second grade students solved the problem:

For each piece of student work [click to enlarge] consider:

• How did the student solve the problem?
• Where in the student’s representation can you see how many rooms are added for each floor? Where can you see the total number of floors?
• What connections do you see between this activity and the operation of multiplication?

Student A	Student B	Student C

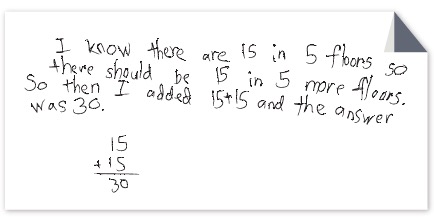As students begin work on situations that involve multiplicative relationships it is helpful for them to work on these relationships in contexts. In this case, maintaining the connection between the context of rooms, floors and buildings, the physical model of the cube building and what is happening with the numbers can help students make sense of the different units, the number of groups (floors) and the number in each group (rooms) and their multiplicative relationship.

Connecting quantities and their relationships in a problem context is directly related to Math Practice 2: reason abstractly and quantitatively.

Read the Math Practices in this Unit essay from second grade about Math Practice 2, reason abstractly and quantitatively, to learn more about how students engage in this math practice as they work with the Cube Buildings context.

Foundational Contexts for Multiplication and Division

Third grade students continue to develop their understanding of the meaning of multiplication. This work begins with modeling and solving multiplication problems in familiar contexts.

After brainstorming contexts for things that come in equal-sized groups of 2 to 10, students use this information to write and solve multiplication problems.

Jot down some things that come in groups of 3. Then read the following problem about things that come in groups of three.

Watch and listen to the following slideshow to learn how students solve this problem at the beginning of third grade.

Consider the ways in which you could use the solutions to Problem 1 to help you solve the following problem:

Watch and listen to the following slideshow to learn some of the ways students might use the solution to the first problem to solve the second problem.

Students use similar contexts as they begin to work on division. They see how these operations are related: that they both involve equal groups, but that different things are known and unknown.

Relating Multiplication and Division

Look at the following Math Words and Ideas: Relating Multiplication and Division. Complete the Try It activity.

Early division strategies closely resemble early strategies for solving multiplication problems, and may include directly modeling the problem using cubes or pictures, skip counting, or using a known multiplication fact.

Read The Relationship Between Multiplication and Division to find out how students use the relationship between multiplication and division to solve problems.

In this activity, you will find all the factors of a number by making arrays; examine ways students use arrays and story problem contexts to represent and make sense of multiplication; and learn about the strategies students use in Investigations to solve multiplication problems.

Students use representations and contexts to:

• make sense of ideas about multiplication and division such as the distributive property
• help them solve problems
• understand and develop strategies
• represent and keep track of their solutions
• develop computational fluency with these operations

Read Images of Multiplication about some of the images and representations of multiplication that students encounter.

Arranging Chairs

Material: 12 coins or similar objects

Third grade students solve “Arranging Chairs problems” as a context to construct the array model for multiplication. Use your coins or other 12 objects you collected to solve the following problem:

• How many different ways could you do this?
• How many chairs would be in each row?
• How many rows would there be?
• What arrangements of chairs will not make an array?
• Did you find all arrays for 12? How do you know?

As students work on Arranging Chairs problems for totals up to 30, they learn about factors and are introduced to the concepts of square numbers (a number with a square array, e.g., 16) and prime numbers (a number with only 2 arrays, e.g., 7 only has 2 arrays: 1 x 7 and 7 x 1).

Array Cards

Third and fourth grade students work with array cards and play a variety of games with them. Array cards have the array on one side with the dimensions and the product and one factor on the other side.

They use these cards to learn multiplication facts, to see how larger problems can be broken into smaller parts and to help them solve multiplication problems.

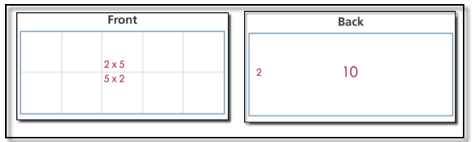
Read Representing Multiplication with Arrays about how students in Investigations use arrays to represent and make sense of multiplication.

Breaking Apart Arrays

Third and fourth grade students work on activities that involve covering larger array cards with two or more smaller array cards. As they do these activities they visually see how larger multiplication problems can be broken into smaller problems.

Material: print grid paper

How can this 6 x 9 array be broken into two smaller arrays? Use the grid paper to show several ways.

Watch the slideshow below to see possible solutions.

Play the following three array card games from third and fourth grade.

Consider:

How does playing these games provide students with opportunities to learn multiplication facts, and see how multiplication problems can be solved by breaking the problems into smaller problems?

Multiplication Cards

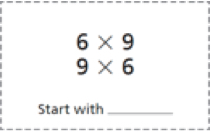
Students are expected to learn the multiplication facts to 10 x 10 by the end of third grade. They learn multiplication facts as they play games with array cards and solve multiplication problems. They also practice multiplication facts using multiplication cards like this one.

Throughout third grade, students work with these cards. They sort the cards into piles of facts they “just know” and facts they are “working on.” Then they look at each fact in their “working on” pile and think of a multiplication fact they already know as a clue. They record the related known fact on the bottom of each fact card - “Start with ________.”

Based on the ways that you saw to break apart the 6 x 9 array what are some possible "start with" clues a student might use to help them with this fact?

Read Learning Multiplication Facts to learn about how students work on multiplication facts in Investigations.

Using Contexts and Representations with Multi-Digit Multiplication Problems

A major focus of fourth and fifth grade students’ multiplication and division work is developing and refining strategies for solving problems with 2-, 3- and 4- digit numbers. Keeping track of the parts of these problems by thinking of equal groups is critical for many students. Story contexts and visual representations help them do that.

One of the story contexts Investigations uses in fourth and fifth grade is teams and players. This simple context can help students visualize the multiplication and division in a problem, make sense of strategies and keep track of the parts when solving a problem.

Solve the following problem.

Multiplication Strategies for 29 x 6

Watch and listen as students share their solutions and later relate their solution to 29 x 6 back to the players and teams story problem context.

Unmarked Arrays

An unmarked array is an array without the grids marked in it. Students use unmarked arrays to help them solve multiplication problems, to represent their solutions, or to help them keep track of the parts of their solution. Watch how students represent their solutions to 6 x 29 on an unmarked array.

Read Multiplication Strategies to learn about the categories of strategies students use to solve multiplication problems.

U.S. Standard Algorithm

Fifth grade students study the U.S. standard algorithm for multiplication and are expected to be able to use it, as well as other strategies, to solve multiplication problems. They begin studying the U.S. standard algorithm by comparing it to other strategies.

Comparing Multiplication Algorithms

Watch the following: Math Words and Ideas: Comparing Multiplication Algorithms.

Consider: How does comparing multiplication algorithms help students develop meaning for the U.S. Standard Algorithm?

Read Studying the U.S. Standard Algorithms to learn about how the study of the U.S. standard algorithms is approached in Investigations.

In this activity, you will examine the Ten-Minute Math Activity, Counting Around the Class, and reflect on how it connects division and multiplication; use a multiple tower to solve problems and relate skip counting work to how students build their understanding of multiplication and division; and examine student work for a division problem.

Understanding that multiplication and division are related operations is important for students to develop efficient and effective division strategies as laid out in the reading The Relationship Between Multiplication and Division, that you read in Activity 1. Many problem situations that we may view as division problems, can be solved using either multiplication or division – a student may view a problem as a multiplication problem with a missing factor, or a division problem with the quotient, or result, unknown.

Counting Around the Class

In the Ten-Minute Math activity, Counting Around the Class, students count around the class by a particular number. Before the count starts, they estimate the ending number of the count and the number the last person in the class will say. During and after the count, students discuss relationships between the chosen factor and its multiples.

Counting Around the Class provides students with practice counting by different numbers and reasoning about the relationships among factors and their multiples. This activity helps students connect multiplication and division equations to multiplicative situations, and supports students in multiplying and dividing with larger numbers. Students also use what they know about multiplication and division to find missing factors.

As you watch the video of a class of 4th grade students engaged in part of the Counting Around the Class activity, pay particular attention to the questions the teacher asks as the students count.

Think about an imaginary class counting by 25.

• What equation represents what the 13th person said?
• When the class finished counting, the last number was 475.
• How many students are in that class?
• What equation represents the number of students in the class?

How does this Ten-Minute Math activity help students see connections between division and multiplication?

Multiple Towers

Multiple Towers is a fourth and fifth grade activity. Students write the multiples of a chosen two-digit number on a roll of adding machine tape. They start from the bottom of the tape and work upward.

In this activity, students examine the relationship between multiplication and division. They focus their thinking on the 10th, 20, 30th (and so on) multiples of a number. Knowing how to find these multiples is useful when breaking apart multi-digit multiplication and division problems.

Multiple towers emphasizes reasoning about multiples as students notice patterns in their towers. Students use landmarks such as the 10th, 20th, 30th or 40th multiple in the sequence – to determine other multiples or factors.

Multiple Towers

Watch the Math Words and Ideas: Multiple Towers.

Use the Multiples of 21 Tower below to solve the following multiplication and division problems.

Watch the following students solve multiplication and division problems using a Multiples of 21 Tower. Notice how the teacher probes the students’ thinking as they justify their solution and discuss connections between other students’ solutions.

Consider: How can the work with Multiple Towers help students understand the relationship between multiplication and division and solve multi-digit multiplication and division problems?

Division

Students use what they learn about the operation of division, the base-ten number system and the relationship between multiplication and division to develop and then become more efficient with strategies for solving division problems.

Solve this division problem from fifth grade. You may want to solve it in more than one way.

Read Division Strategies, which discusses strategies students use when solving division problems.

Look at and analyze the following examples of student work. You may wish to review the LASW protocol for looking at student work to guide your analysis.

Consider for each student.

Does the student:

• break the problem into easily manageable parts?
• solve all the sub-problems (using either division or multiplication) correctly?
• combine the products or quotients of their partial solutions to find the solution to the original problem?
• present his/her solution clearly and concisely?
• correctly identify the remainder?

[Click on each piece of student work to enlarge]

Student A	Student B	Student C

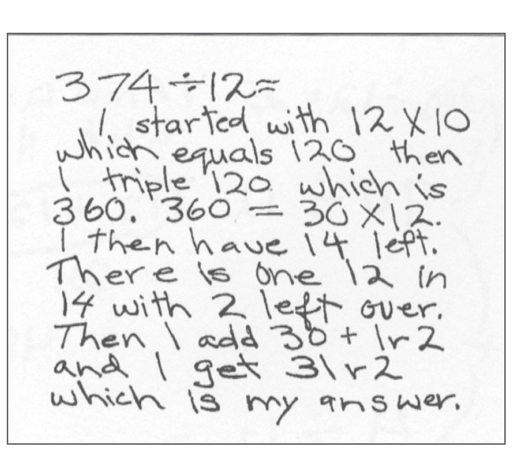In many ways, division is the culmination of work that elementary students do on whole numbers and their operations. For some students, it is also the hardest, and for good reason. To solve division problems accurately and efficiently, students need to be able to hold on to ideas about both numbers and operations, not just the operation of division but the other three as well.

In the Division Solutions Forum share one way you solved 374 ÷ 12, and compare your solution to one of the students’ solutions (Student A, B or C). Once you’ve posted, take a look at other participants’ solutions in the forum.

Once you have completed the work in this session, go to the Session 4 Discussion Forum.

Describe one new thought you had in this session regarding the use of contexts and representations in working with multiplication and division. How might that help you in your work with your students?

• Students use representations and models such as arrays and contexts to help them make sense of and solve multiplication and division problems.
• When students solve multiplication and division problems, they most often use strategies that involve breaking numbers apart to create problems that are more manageable and that make use of familiar number relationships.
• Students learn multiplication and division facts in Investigations by using what they already know about numbers and number relationships and about the properties of multiplication and division and not just simply by rote memorization.
• Understanding the relationship between multiplication and division is important for students to develop efficient and effective strategies to solve division problems.