This session focuses on the areas of geometry and measurement including description and classification of shapes, linear measurement and measurement of area and volume.

You will:

• learn about how students identify and use attributes of shapes to compare and classify shapes
• consider the important aspects of measuring accurately to solve a perimeter problem
• learn how students make sense of area over the grades as they compose and decompose shapes and find the area of rectangles and non-rectangular shapes
• develop a generalizable strategy for finding the area of a rectangle
• look at the work students do around volume

Materials

• Print Area of Polygons

Getting Started: Geometry and Measurement in the Real World

Take a look at your surroundings (e.g., your classroom, your bedroom or any room in your home, in the street or in the world around you), and write down the geometric shapes you notice.

Questions to consider as you do this:

• What attributes does the shape you are noticing have?
• How might you sort the shapes you are noticing?
• How are the shapes you notice related?
• How would you describe a particular shape to someone over the phone?

Next, think about where you use measurement:

• What do you measure?
• How would you measure what you are thinking about?
• Aside from using a unit of measure, what math is involved?

While we study geometry and measurement in school, it’s important to connect that with what we see outside of school. When buying fabric for a sewing project, making a recipe, or building something, you are using what you know about geometry and measurement.

Geometry in Investigations

In Investigations students work on describing, identifying attributes of and classifying shapes from Kindergarten through grade 5. To get a sense of what this work looks over this span of grades read the information below from the Implementation guide for Kindergarten and grade 5.

In this activity, you will look at games and activities in which students examine the attributes of 3-D shapes; sort 2-D shapes by their attributes; consider what students understand about what makes a rectangle; and examine how students’ work on the classification of shapes develops over the grades.

Attributes of 2-D and 3-D Shapes

Kindergarten through fifth grade students describe, sort and classify 2-D and 3-D shapes. They begin by identifying shapes in the world around them, using their own words to describe each shape’s general appearance.

Watch the Kindergarteners in the following clip as they search for and later describe 3-D shapes and relate them to real-world objects. As you watch the video, think about what the students are noticing about the attributes of the shapes.

Geoblocks

A set of Geoblocks consists of rectangular prisms, triangular prisms, and pyramids. K-2 students explore the 2-D shapes on 3-D objects by tracing the faces of Geoblocks and matching those faces to 2-D outlines. As students describe, compare and match faces, and draw Geoblocks, they begin to develop an understanding of attributes of 3-D shapes.

Find a Block

In Find a Block, second grade students match a Geoblock to a 2-D representation of its faces. While a Geoblock is a 3-D solid, each face is a polygon. The 2-D shape of the faces are the focus of this activity. For example, a cube has six square faces. Its Geoblock Task Card has six squares representing each cube face. Its Geoblock Task Card has six squares representing each cube face.

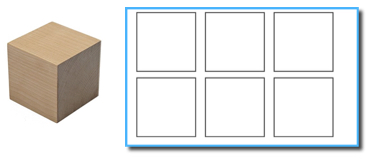
Match the Geoblock image to each Geoblock Task Card in the Geoblock Flipbook.

Sorting 2-D Shape Cards

Students have many opportunities to sort shapes throughout Investigations. First, second, fourth and fifth grade students work with shape cards. These shape cards are different at each grade. Students use these sets and subsets of shape cards in a variety of ways. One of the ways students work with shape cards is to sort the shape cards into categories. As they sort shape cards, they:

• think about their similarities and differences
• begin to identify important geometric characteristics of shapes

Watch as second grade students describe and sort their cards in the following video. Pay attention to the questions the teacher asks as she facilitates this lesson.

Consider:

• How does the teacher in the video encourage students to engage in conversations about the attributes of the shapes?
• What are the students noticing about the similarities and differences among shapes?

Guess My Rule

In Investigations, first, fourth and fifth grade students play Guess My Rule with Shape Cards, a game that focuses on sorting shapes by attributes.

Play Guess My Rule. Find someone to be your partner.

• Click on the Guess My Rule image below to go to the fifth grade online version of Guess My Rule.
• Read and follow the directions located in the tab at the top of the page.
• Play the game at least three different times.

Share one round on the Guess My Rule Forum.

• Take a screen shot of the page with the sorted shapes at the end of the round and upload it onto the Guess My Rule thread in the Forum.
• Try to figure out the rules for three of the Guess My Rule screen shots posted by other course participants. Post your guess or ask the creator some questions to help you determine the rule.

How will this game help the students toward the goal of being able to classify shapes?

Defining Attributes of Shapes

Classifying and defining shapes are important but complex processes in geometry. Students’ work focuses on these processes throughout the grades. For example:

• first grade students consider what makes a triangle a triangle
• second grade students consider what makes a rectangle a rectangle
• third grade students categorize quadrilaterals based on their attributes and compare the properties of rectangles, squares and rhombuses.

Read What is a Rectangle? to learn about the complexities of understanding what a geometric shape is and how it is classified.

Watch as Kindergarten students select squares from a variety of shapes and describe the attributes of a square. Pay attention to how they are deciding whether a shape is a square.

Defining a Rectangle

After sorting shapes in a variety of ways, second grade students work on determining what makes a rectangle a rectangle. They are then assessed on this knowledge.

Feature - Embedded Assessments

Embedded Assessments in Investigations are written activities that provide information on students' progress towards the Benchmarks in a unit. For these assessments students solve problems and show or explain their solutions. These assessments are accompanied by Teacher Notes which provide examples of student work and guidelines for assessing whether students meet, partially meet or do not meet the Benchmark.

Read Assessment: Rectangles which includes pieces of student work sorted into the categories of Meeting the Benchmark, Partially Meeting the Benchmark, and Not Meeting the Benchmark with information about why these pieces of work meet or do not meet the Benchmark.

As you look at the student work samples in the reading, Assessment: Rectangles, think about what it means to meet, partially meet, and not meet the benchmarks, and how that helps the teacher.

Classifying Shapes Across the Grades

As students move through the grades, they work on classifying shapes and defining them in more sophisticated and complex ways.

After the students have had multiple opportunities to build, draw and sort quadrilaterals, they share what they’ve learned and create classification charts based on their discussion.

Look through the FlipBook below for examples of K-5 classification of quadrilateral charts.

As you look through the examples, notice how the work with classification of quadrilaterals develops over the grades.

Quadrilateral FlipBook

Read this Math Practices in this Unit essay which describes how some third grade students engage in Math Practice 3: Construct viable arguments and critique the reasoning of others, as they discuss whether a specific shape belongs in a particular category.

Look at the teacher’s questions/interjections in the vignette in the essay. What was the teacher’s role as students listened to and built on each other’s arguments about what a rhombus is and how it’s related to other shapes?

In this activity, you will learn about the elements of measuring accurately with non-standard and standard units; determine possible perimeters for a given area; and consider how students come up with generalizable methods to determine the perimeter of a rectangle.

Foundations of Measurement

Kindergarten and first grade students learn what attributes of objects can be measured and the techniques, tools, and units used to measure the attributes through their measurement work. Gradually over time, they develop an understanding that length is a stable, continuous, measurable dimension that can be described, compared and quantified.

Students begin by directly comparing objects to determine which is longer and then by measuring the length of objects using non-standard units such as shoe-lengths, craft sticks, cubes and paper clips. As they measure with non-standard and then with standard units they learn and practice foundational skills for accurate linear measurement. These include knowing when to start and stop measuring, lining up units so as not to create gaps or overlaps, and measuring in a straight line from point to point.

Read Learning About Length: Lining Up Units about how Kindergarten students learn about length.

As you read, consider the following questions:

• What are some of the challenges young students face in learning about length?
• How can you support young students in developing their understanding of length, and accurate strategies for measuring length?

Strategies for Measuring Accurately

Watch Math Words and Ideas: Strategies for Measuring Accurately. Make sure to do the ‘Try It’ at the end.

Standard Measurement Tools

Second grade students begin using rulers, yardsticks, and meter sticks to measure lengths in U.S. standard and metric units. Their earlier experiences with nonstandard measurement tools lay the foundation for their work with standard units of measure. They continue to develop the mechanical skills and conceptual understandings needed to measure length with accuracy in third and fourth grade.

Read Making Careful Linear Measurements about the mechanical skills and conceptual understandings students need to measure accurately.

Perimeter

Third grade students learn that perimeter is the distance around the outside edges of 2-D shapes. Third and fourth grade students:

• measure the perimeter of various 2-D objects in the classroom using U.S. standard and metric units
• determine unknown side lengths given the perimeter and the other side lengths of a shape
• create multiple shapes for a given perimeter

Pilar's Yard

Solve the following third-grade problem:

The perimeter of Pilar’s yard is 100 feet.
Draw a picture of what her yard might look like.
Label each side.

Then draw a different yard with a perimeter of 100 feet.

Making generalizations about perimeter

Fourth graders work together to determine generalizable methods for finding the perimeter of rectangles. After finding the perimeter of multiple rectangles given the dimensions of the rectangle, students discuss strategies for finding the perimeter of any rectangle. As they share their ideas for rules and revise and clarify these rules, students engage in Math Practice 6, Attend to precision.

Read the fourth grade Math Practices in this Unit essay about how students enact Mathematical Practice 6: Attending to Precision as they work together to come up with generalizable strategies for finding the perimeter of a rectangle.

In the Math Practices in this Unit essay, what are some examples of students engaging in Math Practice 6?

In this activity, you will learn about K-2 activities that lay the foundation for finding area in later grades; see how students find the area of rectangles and later move towards determining a generalizable method for finding the area of rectangles; and find the area of a non-rectangular shape.

Pattern Block Fill-Ins

Area is the amount of space covered in two-dimensional space. While students do not formally work on measuring area in Kindergarten, first and second grade, as they examine, cover and break up the area inside shapes in various ways, they are working on ideas related to area.

Kindergarten and first grade students fill in outlines of shapes and designs with pattern blocks in a few different activities, including as they play the game Fill the Hexagons. Play a few rounds of Fill the Hexagons.

In the activity, Filling with More and Fewer, students fill in the same design outline with pattern blocks in two different ways, using a smaller number of blocks in one and a larger number of blocks in the other.

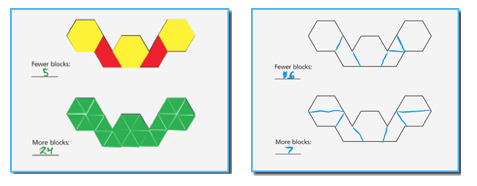
Consider the questions from the Filling with More and Fewer Ongoing Assessment: Observing Students At Work as you look at the following pieces of student work. [click to enlarge]

As students compose and decompose shapes in activities like Filling with More and Fewer and Fill the Hexagon, they:

• notice relationships between shapes
• recognize that you can break up a shape into smaller shapes
• recognize that you can put together shapes to make larger shapes

How do experiences like these help students begin to work on ideas related to area?

Area of Rectangles

A square unit is the standard unit used to measure area. Other units can be used to measure area as long as the same size unit is used to cover the whole area without any gaps or overlaps.

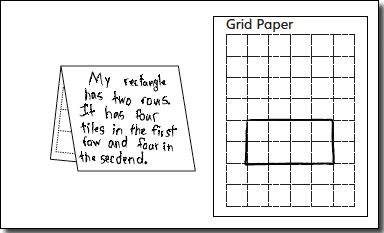
Second grade students touch on the idea of finding the area of rectangles as they begin working with arrays. They draw a rectangle on grid paper and then write a description of it so another student can build it.

In third grade students begin finding the area of rectangles by covering them with square inch tiles. Look at the following strategies for determining the area of the rectangle using tiles.

Read Finding the Area of Rectangles in which the teacher facilitates a discussion where the fourth grade students work together to come up with a generalizable method for finding the area of any rectangle.

• In what ways did examining students’ strategies for a specific problem help them come to a generalizable method?
• Look carefully at the teacher’s questions. How did the teacher’s questions help students move towards finding a generalizable method for finding the area of a rectangle?

Perimeter and Area

Third grade students consider the ideas that shapes with different areas can have the same perimeter and shapes with different perimeters can have the same area as they find the areas and perimeters of a variety of rectangles.

Each of the shapes below has an area of 4 square units. Find the perimeter of each shape.

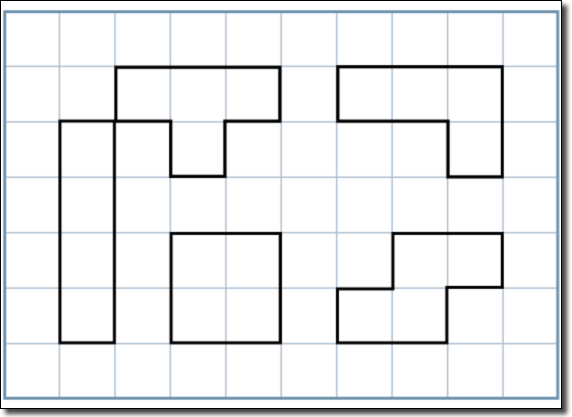
What do you notice about the different perimeters of these shapes that all have the same area?

Finding the Area of a Non-Rectangular Shape in Square Units

Students find the area of shapes that are not rectangles by decomposing the shape into smaller rectangular parts and then combining the areas of the parts.

Print Area of Polygons and find the area of these shapes using the small square as the unit of measure (square centimeters).

In this activity you will examine how students in Kindergarten engage in  work with 3-D shapes that relates to finding the volume of 3-D shapes; find the volume of a rectangular prism; and learn how students engage in MP4: Model with Mathematics as they find the volume of rectangular prisms.

Volume is an essential concept in students’ learning of 3-D geometry. The work students do with volume happens primarily in fifth grade. Kindergarten, first and second grade students become familiar with the structure of 3-D shapes which helps them later with finding the volume of 3-D shapes.

Build a Block

Kindergarten students play a game called Build a Block. They build a block using different combinations of blocks.

Build a Block

Watch Math Words and Ideas: Build a Block. Complete the ‘Try It’ activity.

How might activities like Build a Block help students with finding the volume of solids in 5^th grade?

Volume of a Rectangular Prism

Students learn that the volume of a solid is the space that the solid occupies. To understand the measurement of volume and why it is measured in cubic units, students first develop strategies for determining the number of cubes in 3-D arrays.

Determine how many cubes make up this solid.

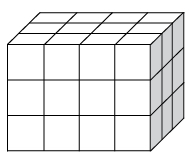
How did you determine the volume of the solid?

Look at the responses below from a fifth grade class with limited exposure to 3-D geometry activities. Select at least three student responses below to examine. How do you think students might have arrived at their predictions?

Read Strategies for Finding the Number of Cubes in 3-D Arrays to learn how students may mentally construct an image of a 3-D array.

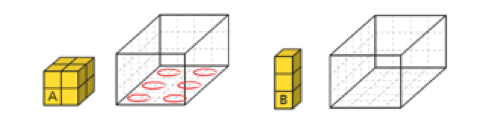
In Investigations, fifth grade students work on volume using the context of a packaging factory. They determine how many cubes fit in open-top boxes without the box lid and then check by building the box and filling it with cubes.

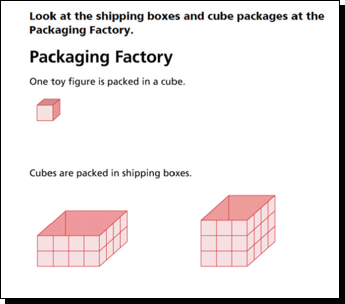
Next, they determine how many packages made up of multiple cubes fit in the open boxes.

They also find the volume of their classroom using cubic meters, yards or feet.

Read the fifth grade Math Practices in this Unit essay. It describes how fifth grade students engage Math Practice 4: model with mathematics, as they find the volume of rectangular prisms.

Consider: How does the work students do building the 3-D arrays and using the layering approach described in the reading help students make sense of the volume formulas: V = b x h or V = l x w x h?

Once you have completed the work in this session, go to the Session 5 Discussion Forum.

What do you think students need to be able to understand in order to classify shapes and measure them? (You can focus on a few different elements in your post, or focus on one element).

• Students identify important attributes of shapes as they sort and compare shapes. They use this knowledge to then classify and define shapes.
• As students measure with non-standard and standard units they learn what is involved in measuring accurately.
• Gradually over time, students learn that length is a stable, continuous, measurable dimension that can be described, compared, and quantified.
• Students learn about geometric relationships as they compose and decompose shapes. Composing and decomposing shapes are foundational ideas that students apply to find the area and volume of shapes.
• Students measure the perimeter, area and volume of shapes by first measuring with tools - rulers, one inch tiles and cubes - and counting. They gradually move towards using generalized methods involving addition and/or multiplication as they find measurements of perimeter, area and volume.