
Overview
Session Summary
This session focuses on the operations of addition and subtraction in the Investigations curriculum for Kindergarten through second grade. Participants consider how students work on important aspects of solving story problems: making sense of the action of the problem, solving the problem in ways that make sense, and recording their strategies so that others can see how they solved the problem. They examine the different strategies students use to solve addition and subtraction problems and how those strategies develop over time. They learn about the work students do with number composition, addition combinations and place value, and how these are building blocks for the development of strong, efficient strategies for solving addition and subtraction problems.
This session is part one of two sessions about addition and subtraction in the Investigations curriculum. This session focuses on addition and subtraction in Kindergarten through second grade. We will look at how students work on story problems, the strategies students use to solve addition and subtraction problems, and the work students do with decomposing numbers and place value that helps them develop efficient strategies for solving addition and subtraction problems. In the second session on addition and subtraction you will look at the work that students do in grades three through five of Investigations.
Mathematics in this session
- Visualize, retell and model the action of addition and subtraction situations
- Examine strategies for solving addition and subtraction story problems
- Decompose numbers in different ways
- Work with place value, including breaking numbers up into tens and ones
- Consider how students develop fluency with two-addend combinations up to 10 + 10
Common Core Alignment
The content in this session is aligned to the following Common Core State Standards and Math Practices:
Operations and Algebraic Thinking
- Understand addition as putting together and adding to, and understand subtractions as taking apart and taking from (K)
- Represent and solve problems involving addition and subtraction (1 and 2)
- Understand and apply properties of operations and the relationship between addition and subtraction (1)
- Add and subtract within 20 (1 and 2)
- Work with addition and subtraction equations (1)
- Work with equal groups of objects to gain foundations for multiplication (2)
K.OA.1-5
1.OA.1-8
2.OA.1, 2
Number and Operations in Base Ten
- Work with numbers 11-19 to gain foundations for place value (K)
- Extend the counting sequence (1)
- Understand place value (1 and 2)
- Use place value understanding and properties of operations to add and subtract (1 and 2)
K.NBT.1
1.NBT.2abc
1.NBT.4-6
2.NBT.1ab, 2.NBT.5-9
2.MD.5
MATH PRACTICES
MP1: Make sense of problems and persevere in solving them.
MP5: Use appropriate tools strategically
MP6: Attend to precision
You may also wish to review the full set of Common Core State Standards in Math and/or videos of the Math Practices enacted in Investigations.
Readings
Story Problems in Kindergarten, from Unit KU2 – Counting and Comparing (Grade K)
Three Approaches to Story Problems, from Unit IU3 – Solving Story Problems (Grade 1)
Adding With Stickers, from Unit 2U6 – How Many Tens? How Many Ones? (Grade 2)
Place Value in Grade 2, from Unit 2U6 - How Many Tens? How Many Ones? (Grade 2)
Additional Resources
ELL resources - TBD
In this introductory activity you are asked to solve a problem mentally. After you have solved it, write down your steps (on paper or electronically) to remember them.
School Assembly Problem:
475 students attended an assembly at the Mitchell school. 89 students left early to go on a field trip. How many students were still at the assembly?
What strategy did you use to solve the problem? Can you think of a different approach than the one you used?
Once you have brainstormed one or more strategies, click the Show link to review other possible solutions.
Some possible solutions include:
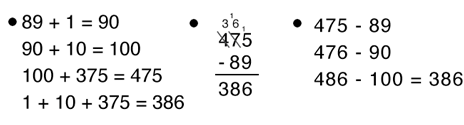
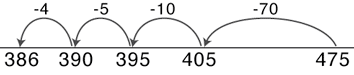
NOTE: The open number line is a tool that people sometimes use to solve and/or record an addition or subtraction strategy.
What did you need to know or understand about addition or subtraction or about numbers in order to solve this problem using these strategies?
Note: We want 4th and 5th graders to have a few different strategies they can efficiently and flexibly use to solve addition and subtraction problems.
In order to solve problems efficiently and flexibly students need to develop building blocks of computation. This work is begun in the early gradesBeginning in Kindergarten, students solve addition and subtraction story problems. This work on addition and subtraction story problems continues throughout the grades and is an essential part of the Investigations curriculum. In this activity you will learn about the focus of the story problem work students do in Investigations. You will view a video and sort student work according to the approaches students used to solve some story problems.
You will begin by viewing a video that illustrates how a teacher might introduce a story problem to a group of students.
Here is a story problem students might solve in first grade:
Last night I picked up 12 pencils from the floor. I put 4 of the pencils in the pencil box. How many were left in my hand?
When students are introduced to a problem they are asked to visualize what happened in the story, retell the story and think about whether there are going to be more or fewer pencils at the end of the story.
As students work on story problems, the focus is on students making sense of the action of different types of addition and subtraction problems and developing strategies to solve them. Listen to the comments in the VoiceThread below for additional insight on the focus in helping students solve story problems.
EQUITY MOMENT
Story problems can be particularly challenging for students whose first language isn’t English. Brainstorm different ways to support English language learners. Some ideas you touch on could include: acting out stories, using manipulatives, reviewing new vocabulary, using pairs or small groups to explain the story, and having students write their own stories.
You may also wish to explore the following optional resources to leawrn more about supporting ELL students in working with story problems: (Add additional resources when they are ready)
Three Approaches to Solving Story Problems
When students solve problems in ways that make sense to them, they use a few different approaches. These approaches are based on each student’s understanding of number and of the specific operation.
Young students commonly take one of three approaches to solving a story problem: counting all, counting on or back, or numerical reasoning. Learn more about these three approaches by clicking the Show link.
Include in the Show/Hide the three slides associated with Transparency 5, and please make the edits included in the AS1_Session_2009_with comments for team.doc document.
More in depth explanations and additional student work illustrating each approach can be found in Teacher Note, Three Approaches to Story Problems.
EQUITY MOMENT
Studies suggest that there seem to be gender differences in problem solving strategies. Carr and Jessup found that girls were more likely to use overt strategies (counting on fingers or with counters), while boys were more likely to use retrieval (from memory) to solve addition and subtraction problems. In the group sessions, all children were more likely to use covert strategies, e.g., mental calculation and retrieval. What ideas do you have about how to support all students in being flexible problem solvers?
[SORTING STUDENT WORK ACTIVITY FROM MIKE AND CAROLYN GOES HERE]
NOTE: Research has shown that children tend to begin to use counting on more often than counting all and then reason numerically more often than counting. However, just as we do, they use a range of approaches at the same time depending on the difficulty of the problem.
EQUITY MOMENT
When looking at student work, teachers often use the adjective “better” when comparing and assessing student work. This is a subjective description; instead, we are trying to look for levels of mathematical efficiency. All students should be expected to achieve at high levels and to master more efficient strategies. One way to think about high expectations for all students is to: 1) appreciate and acknowledge where a student currently is and 2) figure out where you want the student to go and how you can help him/her get there.
The strategies students use in later grades to solve problems with larger numbers grow out of the strategies students are using in the early grades. You will examine strategies that students use to solve addition problems with larger numbers at the end of this session and the strategies students use for solving subtraction problems with larger numbers in the Addition and Subtraction, part 2, session.
In this activity you will practice using two games focused on number composition and discuss the mathematics in the games. You will also look at examples of how students use addition cards and think about how the games help students develop fluency with addition combinations.
In Kindergarten through second grade, students work a lot on number composition. For example, in first grade when students solve a problem about 12 crayons - some are red, some are blue - they may find out that 12 is composed of 6 and 6, but it can also be 5 and 7. In a game called Ten Plus students see that 8 + 4 or 12 is equivalent to 10 + 2. When Today’s Number is 12 they might break it into three parts: 4 + 4 + 4.
Working on number composition encourages flexibility with numbers, helps students learn addition and subtraction facts and exposes them to ideas about place value.
You will now view sample “hands” of two games that focus on number composition: How Many Am I Hiding? - a 1st grade game, and Make Ten – a game that is in both 1st and 2nd grades (a version of this game called Make 6 is in Kindergarten).. Games are an integral part of the Investigations curriculum. When students play games multiple times they can deepen their understanding of numbers and the operations and practice computation.
- What are students practicing in this game?
- What other math ideas do students encounter in this game?
- What are the range of strategies you expect students to use to play this game?
As students compose and decompose numbers they are learning about number composition and the operations of addition and subtraction. As they play games like these they are also beginning to learn addition combinations or facts. For example, after students play Make 10 multiple times they often remember many of the combinations that make 10: 1 + 9, 2 + 8, 5 + 5, etc.
In 2nd grade students also use addition cards to work towards becoming more fluent with addition facts. They learn addition facts in categories (all of the doubles combinations, all of the 10s combinations, etc.). As they work with the addition cards for a category they also do activities that focus on those particular combinations (e.g., playing Make Ten while practicing the 10s combinations). They use the addition cards to think about what combinations they already know and to practice those they don’t know. To help practice the combinations they find difficult they write clues to help them remember them.
Students learn combinations best by using strategies and not just simply rote memorization. If students use their understanding of numbers and number relationships to work on combinations then they have ways to figure out combinations when they can’t remember them.
Refer to Teacher Note, Learning the Addition Combinations for more information on how students learn the combinations.
EQUITY MOMENT
Are there some students that typically do better in math when activities are framed in terms of competition? Cooperation? Does this break down along gender lines? In what ways can you help students feel more comfortable in various situations? What management techniques do (or can) you employ?
In past workshops, many participants have said that typically boys engage more readily when the activities involve competition and girls “do better” when activities involve cooperation. However, many participants have said that over the last few years, girls have become more competitive in classrooms.
Some students naturally work more slowly than others. What role does speed play in how students approach and complete math problems? What implication does this have for classrooms? Does the person who completes an activity faster “win”? Do you notice issues of speed breaking down along gender lines or other variables (including confidence and experience)? How can you provide opportunities for students working at various paces to work at their pace while also being participatory in whole group work and discussions?
In this activity you will solve an addition problem in the Sticker Station context and look at students’ strategies for solving the same problem. Then you will solve another problem using one of the strategies the students used.
Work on number composition includes work on breaking numbers into tens and ones. This is a part of learning about place value. Earlier we saw an example from the game Ten Plus in which students find an equivalent expression with one of the addends being ten. In grade 2 students are introduced to a sticker station context to work on ideas about place value and the way numbers are structured using tens and ones. This context is revisited in grade 3.
Sticker Station
In the Sticker Station context, there is a store that sells stickers and the stickers are sold in different ways: single stickers, strips of 10 stickers, and pages of 100 stickers (which students are introduced to later). Students in second and third grade solve a variety of problems based in this context of the Sticker Station.
Students begin by finding all the different ways someone can have 46 stickers. What is one way you can have 46 stickers? How many strips of ten? How many singles? What is a different way?
Here are two different ways to make 46 stickers using sticker notation. The lines stand for one strip of ten and each dot stands for a single sticker.
Students find out that, for example, the number 46 is not only 4 tens and 6 ones but also 3 tens and 16 ones.
Note: While the visual representation of the stickers is nearly the same as the Base Ten Blocks, the field test for the revision of Investigations showed that second graders are more likely to connect with the specific context of stickers.
Next, please solve the following problem mentally in any way that works for you.
Franco had 66 car stickers. Jake gave him 52 car stickers. How many car stickers does Franco have now?
Click through the screencast below to see several options for how this problem can be solved.
[BEGIN SCREENCAST ACTIVITY HERE] 66 + 50 = 116 [IMG] 116 + 2 = 118Other strategies participants might share include:
• 60 + 50 = 110 [IMG] 6 + 2 = 8 110 + 8= 118 • 52 + 50 = 102 [IMG] 102 + 16 = 118Students’ Strategies
Earlier we saw how students solved problems using counting all, counting on, and numerical reasoning. As students gain a better understanding of the structure of the base ten number system, they apply this knowledge to develop strategies for solving addition and subtraction problems.
[INCLUDE STUDENT WORK/ANNOTATION ACTIVITY HERE]Display Transparency 14: Addition Strategies: Holly’s and Henry’s Work.
Display Transparency 15: Addition Strategies: Chen’s and Simon’s Work.
Holly and Henry used the strategy of breaking up both numbers into tens and ones. In Investigations this strategy is called adding tens and ones or adding by place. Holly added the tens and ones separately while Henry added the tens together and then added on the ones from one number and then the ones from the other number.
Both Simon and Chen used the strategy of keeping one number whole and breaking the other number into parts. In Investigations this strategy is called keeping one number whole. Simon and Chen broke up the 52 in different ways – Chen broke it up into 5 tens and a 2 and Simon broke it up into 4, 40 and 8.
There are other strategies that students may use to solve addition problems but these two are the main ones.
Solving Another Problem
Finally, solve the following problem using either an adding by place strategy or a keeping one number whole strategy.
48 + 37Note how you solved the problem. Which strategy did you use?
Discussion
In this session, you explored a number of different strategies students may use when solving addition and subtraction problems. Pick one of the strategies that emerged from this session and share what you learned about the mathematics students are using when engaging that particular strategy. In thinking back to the building blocks of computation (link to slide) that were introduced at the beginning of the session, how does this strategy support students’ development of these building blocks?
Key Learning
- We want 4th and 5th graders to have a few different strategies they can efficiently and flexibly use to solve addition and subtraction problems.
- In order to solve problems efficiently and flexibly students need to develop building blocks of computation. This work is begun in the early grades.
- (We can add more bullets – this is just a start)
This session is aligned with the following K-2 Units in Investigations