Overview

Session Summary

In this session you will learn how, in the Investigations curriculum, students work on some of the important ideas in 2-D Geometry: decomposing and composing 2-D shapes, finding the area of a 2-D shape and sorting and defining shapes. You will explore a game for sorting a variety of quadrilaterals according to their attributes. You will then fill in shape outlines with smaller shapes in different ways. Finally, you will determine the area of a set of shapes including the area of two different triangles and consider the concepts about area that students work on throughout the grades. Throughout the session you will have the opportunity to see student work.

We all have had different experiences in working with geometry. For some of you, geometry may have been an area you gravitated towards, while for others geometry may have been a math subject you found more challenging. This is true for your students as well. You may find that there are some students in your class who struggle in working with numbers, but who flourish in the area of geometry. It might help these students to try to link what they are learning in geometry to their work in number. You may also have students who work with numbers with ease, but find geometry difficult. We hope that providing students with rich experiences in geometry from an early age will help all students develop their spatial understandings and visualization skills.

Why Study Geometry?

There are a number of ways students are likely to use geometry and visual thinking in "the real world,” in work, and in school. These include:

• Geometric models are critical in understanding number relationships
• Visualizing models is essential throughout the study of mathematics and science
• Visual skills are central in many occupations, including design, engineering, manufacturing, and construction
• Interpreting 2-D representations of 3-D models becomes more and more important as tools (such as computer-aided design) become more and more visual

Mathematics in this session

• Compose and decompose shapes in different ways
• Find and compare the areas and perimeters of shapes
• Sort shapes according to their attributes
• Identify important features of a shape

Common Core Alignment

The content in this session is aligned to the following Common Core State Standards and Math Practices:

CONTENT STANDARDS

Measurement and Data - K.MD, 3.MD

Classify objects and count the number of objects in each category.

3. Classify objects into given categories; count the numbers of objects in each category and sort the categories by count. (K)

Geometric measurement: understand concepts of area and relate area to multiplication and to addition. (3.MD)

5. Recognize area as an attribute of plane figures and understand concepts of area measurement. (3)
   1. A square with side length 1 unit, called “a unit square,” is said to have “one square unit” of area, and can be used to measure area.

7. Relate area to the operations of multiplication and addition. (3)
   4. Recognize area as additive. Find areas of rectilinear figures by decomposing them into non-overlapping rectangles and adding the areas of the non-overlapping parts, applying this technique to solve real world problems.

Geometric measurement: recognize perimeter as an attribute of plane figures and distinguish between linear and area measures.

Geometry - K.G, 1.G

Identify and describe shapes (squares, circles, triangles, rectangles, hexagons, cubes, cones, cylinders, and spheres). (K)

1. Describe objects in the environment using names of shapes, and describe the relative positions of these objects using terms such as above, below, beside, in front of, behind, and next to. (K)
2. Correctly name shapes regardless of their orientations or overall size. (K)

Analyze, compare, create, and compose shapes

6. Compose simple shapes to form larger shapes.

Reason with shapes and their attributes - 1.G, 2.G, 3.G

1. Distinguish between defining attributes (e.g., triangles are closed and three-sided) versus non-defining attributes (e.g., color, orientation, overall size); build and draw shapes to possess defining attributes. (1)
2. Compose two-dimensional shapes (rectangles, squares, trapezoids, triangles, half-circles, and quarter-circles). (1)
3. Partition circles and rectangles into two and four equal shares, describe the shares using the words halves, fourths, and quarters, and use the phrases half of, fourth of, and quarter of. Describe the whole as two of, or four of the shares. Understand for these examples that decomposing into more equal shares creates smaller shares. (1, 2)

1. Understand that shapes in different categories (e.g., rhombuses, rectangles, and others0 may share attributes (e.g., having four sides), and that the shared attributes can define a larger category (e.g., quadrilaterals). Recognize rhombuses, rectangles, and squares as examples of quadrilaterals, and draw examples of quadrilaterals that do not belong to any of these subcategories. (3)

Draw and identify lines and angles, and classify shapes by properties of their lines and angles. - 4.G

2. Classify two-dimensional figures based on the presence or absence of parallel or perpendicular lines, or the presence or absence of angles of a specified size. Recognize right triangles as a category, and identify right triangles. (4)

Classify two-dimensional figures into categories based on their properties. - 5.G

3. Understand that attributes belonging to a category of two dimensional figures also belong to all subcategories of that category. For example, all rectangles have four right angles and squares are rectangles, so all squares have four right angles. (5)

MATH PRACTICES

MP1 Make sense of problems and persevere in solving them.

MP3 Construct viable arguments and critique the reasoning of others.

MP6 Attend to precision.

You may also wish to review the full set of Common Core State Standards in Math and/or videos of the Math Practices enacted in Investigations.

Sorting Shapes

Overview

In this activity you will explore a game for sorting shapes according to their attributes. You will then look at some second grade student work in which students explain how they know whether a shape is a rectangle.

Guess My Rule

Throughout the grades, students sort shapes according to their attributes. One of the activities that focuses on sorting by attribute which is used in first, fourth and fifth grades is Guess My Rule. Watch the VoiceThread below to explore sample rounds of Guess My Rule.

After watching the VoiceThread, you may want to cut out your own quadrilateral shape cards to play Guess My Rule with a colleague or students.

Sorting Shapes

Students sort shapes in first, second, fourth and fifth grade. These are the work of first graders who were asked to sort a set of shape cards in different ways and then to display on a poster one way they sorted the cards.

Students are encouraged to describe shapes and attributes of shapes in ways that make sense to them. They may describe shapes using

• conventional geometric vocabulary ("triangle,” “vertex," "acute angle") or
• non-mathematical terms ("looks like a roof,” “ pointy," "corner").

As you model the use of geometric terms while students work on the activities in a geometry unit, they will begin to use some of those geometric terms themselves.

Students have many opportunities to sort shapes throughout the Investigations curriculum. As they sort shapes they

• think about their similarities and differences and
• begin to identify important characteristics of shapes.

This focus leads to classification and definition of shapes – important processes in geometry. For example, first graders consider what makes a triangle a triangle. Second graders consider what makes a rectangle a rectangle. And fourth graders consider what makes a polygon a polygon.

Video

In this video, Kindergarten students are selecting squares from among a variety of shapes, and describing the attributes of a square when they are not sure whether an object is a square.

Defining Shapes

In second grade, after sorting shapes in a variety of ways, students work on defining what makes a rectangle. They are then assessed on this knowledge.

These are two students’ work on the 2nd grade assessment. As you review the work, consider the following questions:

• What does Student A understand about the definition of a rectangle?
• What does Student B understand about a rectangle?
• What doesn’t Student B understand about a rectangle?

You may wish to review the DIET protocol for looking at student work before reviewing the examples above.

Pattern Block Fill-Ins

Overview

This activity focuses on the work students do filling in shape outlines with pattern blocks in Kindergarten, first and second grades. Using an applet, you will fill in the same shape outline with more and fewer blocks and consider the mathematics in this activity. You will then learn about other activities that focus on decomposing and composing shapes using shape outlines and pattern blocks that students do.

Filling with More and Fewer

In this activity, you are going to fill a shape outline in two ways – with more blocks and with fewer blocks. Take a look at the shapes on these pages, print them if you wish, and start with any one you like. Using the Pattern Blocks applet, recreate the shape with “fewer blocks” and “more blocks”. When you have finished working on the first shape, choose another one.

To fill a shape with more blocks, some of you may have replaced a block with some smaller blocks. For example, you may have replaced a hexagon with six triangles. You could say that you decomposed the hexagon shape into six triangles. Some of you may have filled in an outline with fewer blocks by combining blocks. For example, you might have put a rhombus and a triangle together and replaced them with a trapezoid. You could say that you were composing shapes.

Composing and decomposing shapes is an important part of the geometry work that students do throughout the grades in Investigations, but particularly in the lower grades. One of the ways that students work on composing and decomposing shapes in Kindergarten, first, and second grades is by filling in shape outlines with pattern blocks like in the activity you just did. While students do pattern block fill-in activities in all three grades the emphasis of each activity is different.

Looking at Student Work: Different Ways to Fill

One of the activities students do in first grade is called Different Ways to Fill. Students fill in the same shape in different ways. The emphasis is on finding different combinations of shapes that fill the same area. Review one student’s work from this activity. This leads to the activity Filling with More and Fewer. The emphasis of Filling with More and Fewer is on using different shapes to fill in the same area with more and fewer pieces.

Students also have an opportunity to fill in shape outlines with smaller shapes on the computer. In grades K-2 there is a computer program called the Shapes Software. One activity in this software is called Puzzles for which students fill in shape outlines with pattern blocks, Power Polygons or Tangrams. These puzzles not only give students more opportunities to work on filling in shape outlines, but also require them to be more precise and aware of their actions – for example, instead of intuitively turning a block with their hand to fit, they have to select a tool to turn or flip it and decide how much of a turn is needed.

Area and Perimeter of Shapes on a Geoboard

Overview

In this activity, you will partition dot paper 4 x 4 squares (or geoboards) into halves, and consider how you know the areas of the halves are the same. You will also find the area of a polygon drawn on dot paper.

This is an activity focused on measurement. Geometry and Measurement are interconnected strands. In Investigations students measure the area of shapes, the perimeter of shapes, the angles of shapes and, in 3-D geometry, the volume of shapes. When students fill in shape outlines with pattern blocks this is also beginning work on the concept of area. They are covering the area of a shape with smaller shapes. Beginning in second grade, students find the area of shapes using a standard unit, usually a square unit.

In this activity, you are going to be measuring and comparing the area and perimeter of shapes. One way to distinguish between area and perimeter is to think about work you might do in your home. If you wanted to get a carpet to completely cover the floor of a room you would need to know the area of the room. If you wanted to install trim along the base of the wall all around the room you would need to know the perimeter of the room.

Using Geoboards

You can practice with Geoboards either using a printed handout and/or by using an online Geoboard applet.

Try filling the square in many different ways, with no two halves that are just rotations or mirror images of one another. The cuts may be zigzags but they must be made of straight lines between dots as if the lines are rubber bands stretched between pegs on the geoboard. The cuts should result in only two parts. If you cut on the lines you draw, the square should break into only two pieces.

After you have spent 5-10 minutes creating halves in different ways, click the Show button below to see examples of how other teachers have created halves. Look carefully. Are there any examples that aren’t halves? How do you know?

In Investigations, Second Edition, students find halves and fourths of a 4 by 6 rectangle. In the fraction session you will be working on fractions of a 4 by 6 rectangle.

Area of a Quadrilateral on a Geoboard

Using the small square as the unit of measure, find the area of the quadrilateral in this diagram and explain on paper how you know the area. You can print out the diagram and write and draw on it as part of your explanation.

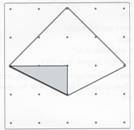
When you have finished, find the area of this triangle (shaded, at right).

Watch the videos below to see examples of how others solves this problem.

There are several main concepts having to do with area that students work on in the Investigations curriculum. What concepts did you work on as you found and compared the areas of shapes on the geoboard?

Perimeter of Halves

Finding the perimeter of a shape on the geoboard that includes a diagonal line is much more complex since the measure of a diagonal line between two pegs is not 1 (it is actually the √2).

When you have finished, find the perimeter of the two halves in this diagram.

Discussion

What have you learned about the connections between students’ work with geometry and work with number?

Key Learning

• Visual skills are central in many occupations, including design, engineering, manufacturing, and construction. Geometric models are critical in understanding number relationships.
• As students sort shapes they think about their similarities and differences and begin to identify important characteristics of shapes. This focus leads to classification and definition of shapes – important processes in geometry.
• A major idea of geometry is that shapes can be combined or decomposed to make other shapes. As students compose and decompose shapes they learn about geometric relationships. Much of what we understand about shapes is based on our knowledge of how shapes are related.
• Different shapes can have the same area. A shape can be decomposed into smaller shapes, and the area of the smaller shapes can be combined to find the area of the larger shape.

This session is aligned with the following K-2 Units in Investigations.

Note about software

The computer software that can be used throughout the year at each grade level is introduced in the 2-D Geometry units. The software used in Kindergarten through second grade is called the Shapes Software. In this software, students work with pattern blocks, power polygons and tangrams to build on the work they are doing in the 2-D Geometry unit and to experiment with geometric transformations (rotations, translations, reflections), explore patterning, and investigate symmetry.

The software used in third through fifth grade is called Logo Paths. In this software students write commands to direct a turtle (a cursor) to move and turn to make shapes and designs. This builds on the work they do with 2-D geometry and measurement and gives them the opportunity to explore geometrical relationships, especially focusing on angle, length and perimeter, patterns in sides and angles, and characteristics of specific shapes.