Overview
Session Focus
In this session you will consider ongoing assessment for learning and its impact on instruction. You will watch teachers as they assess their students’ understanding in different settings –playing a game, solving a problem, during a whole group share and by looking at their written work. You will consider what a teacher can learn through these interactions that informs their teaching and reflect on your own teaching practices.
It’s not enough just to ask the questions. You have to listen and be able to make sense of what kids are saying and what it tells you about what the students understand.”
In mathematics, as in any subject, teachers continually assess students’ strengths and needs and think through how best to accommodate differences to involve all students in substantive and challenging work. All students should be expected to achieve at high levels and to master more efficient strategies.
One way to think about high expectations for all students is to appreciate and acknowledge where a child currently is, and to figure out where you want her to go and how you can help her get there. To accomplish this, teachers must:
- Know the curriculum. Study how the mathematical ideas build over many lessons. Take the time to understand the mathematics focus in each unit and of each lesson.
- Know the mathematics. It’s important to understand how mathematical concepts ideas develop across the grades. Develop a solid understanding of mathematics content, how students learn, and effective, age appropriate pedagogy.
- Know the students. Observe students at work, listen to their discourse, and develop an understanding of their mathematical ideas by analyzing what they say and do.
- Have a plan. To find out what students are doing, and find examples of different strategies to share during the discussion, having a ‘game’ plan is key.
- Establish classroom norms early on. Students work independently alone or in groups, they are expected to communicate their reasoning and listen to that of others, and they see mistakes as opportunities for learning. The environment is one where students can take risks and learn.
- Ask questions that push students to explain their solution, clarify their thinking, or uncover a mistake.
Read Formative Assessment (NCTM)
How are summative and formative assessments different?
The difference between summative and formative assessments is not a function of types of either. It is about how they are used.
- Formative applications of assessment are used to help student and teacher know where the student is headed, where they are now and how to close the gap.
- Summative uses ask, “did the student get there?”
- Any assessment can be used either way, depending on the context. But I prefer to keep them separate. When in a formative context, I want the grade book closed.”
Formative assessments help the teacher learn what students know and understand – a snapshot in time. This information enables the classroom teacher to make appropriate instructional decisions and provide tangible feedback to students during learning. Students can also self assess and play an active role in their learning.
Gathering information
A teacher may gather information by:
- watching students engaged in their work, individually or as part of a group
- listening to student conversations as they work in small groups or pairs
- asking students to share their work and justify their thinking– in print and/or with tools; in the context of a game or story problem
- asking clarifying or probing questions to better understand their thinking
Deciding which students to observe
Teachers may select a student or a group of students to observe as they work with a targeted focus in mind, such as:
- What do they know so far?
- What strategies are they using?
- How do students communicate their thinking and reasoning?
- Are they able to extend their thinking?
- Can students use what they know to make generalizations?
- How flexible are they in their reasoning?
Getting Started: Assessing in the Moment
Teacher observations are an important part of ongoing assessment. Although individual observations may be little more than snapshots of a student's experience with a single activity, when considered together over time, they can provide an informative and detailed picture. These observations can be useful in documenting and assessing a student's growth and offer important sources of information when preparing for family conferences or writing student reports.
Before the lesson, review the lesson and consider what you want to learn about your class or a group of students. Identify a focus and a few questions you think about as you observe. Example: “What strategies are the students using?” As you observe you may use or rephrase the focus question to ask students to clarify or better what they are doing and thinking. Examples: “What strategies are you using?” “Show me how you solved the problem.”
Decide how you plan to record and keep track of your observations of students. The most important aspect of a record-keeping system is that it be both manageable and useful for you. Some teachers:
- Jot down observations of students’ work on a class list of names. Because the space is somewhat limited, it is not possible to write lengthy notes; however, when kept over time, these short observations provide important information.
- Place stick-on address labels on a clipboard. Take notes on individual students and then peel these labels off and put them in a file for each student.
- Jot down brief notes at the end of each week. Some teachers find that this is a useful way of reflecting on the class as a whole, on the curriculum, and on individual students. Planning for the next week's activities can benefit from these weekly reflections.
- Use technology such as a camera, smartphone, tablet or audio to document students as they work. The advantage of documenting is that you can review the student working at a later time. Most schools require parental permission to record students.
- Collect portfolios that might include observation checklists, digital recordings of students at work, student work on written assessments, and other examples of students’ written work.
The first step of an assessment plan is preparing to begin with the end in mind. This means deconstructing the curriculum outcomes or standards into groups of 'big ideas' that make sense for you and your learners. Then think about how best to express the collection of standards in each grouping in learner-friendly language. Research and practice support this powerful idea.”
The second grade teacher in this video describes what he does to informally assess students as they work.
From the Field
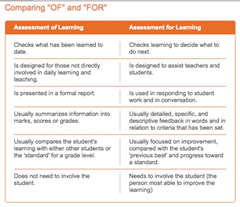
Assessment for Learning and Assessment of Learning
- Assessment for learning is the big deal, while assessment of learning is the done deal.
- Assessment for learning is formative, while assessment of learning is summative.
- Assessment for learning is supportive, while assessment of learning measures.
- Assessment for learning uses descriptions, while assessment of learning uses scores.
- Assessment for learning happens day by day, moment by moment, while assessment of learning happens at the end.
The assertion is that neither one is better than the other, but both need to be used within a students learning so that the student is able to understand not only the work that is being asked of them, but also how their own learning occurs. Assessment for learning is intended to be both diagnostic and formative to help students improve their learning.
Assessing for Learning, Bryan Funk (2009) This Page was edited by Kari Duffy (January 2010)
Table developed by Ann Davies, PH.D. author Making Classroom Assessment Work, Solution Tree, 2011
Readings
- Assessment for Learning
webpage created by Bryan Funk (2009) and edited by Kari Duffy (January 2010) - Formative Assessment: Position of the National Council of Teachers of Mathematics
Question: What is the role of formative assessments in mathematics education? - From Formative Assessment to Assessment FOR Learning: A Path to Success in Standards-Baased Schools Rick Stiggins, Phi Delta Kappan, December 2005
- My Favorite No, Leah Alcala, Teaching Channel
Interview Assessments
Assessing Math Concepts K-3
These assessments were developed by Kathy Richardson
Math Reasoning Inventory
The MRI assessments were developed by Marilyn Burns
The following video clips used in this session are included with My Kids Can: Making Math Accessible for All Learners, K-5, Judy Storeygard, editor, Heinemann 2009
Overview: Teacher interview
Activity 1: 2nd Grade Story Problem
3rd Adding with Three Digit Numbers
CCSS MP Documents
Activity 1: Observing Students - Listening and Noticing
In this activity you will watch teachers assess in three different settings – during a game, as students work independently on a problem and in a small guided group setting. The students are engaged in their regular math work of the day. These teachers represent different grades, different settings, different situations, and they have different goals. Still you will notice some commonalities.
You will do some math and predict how students might approach the same tasks before you watch the video clips. As you engage in the math activities and watch the classroom video clips, think about:
- the math the students are working on
- anticipate what they might do and say
- how you would support their learning
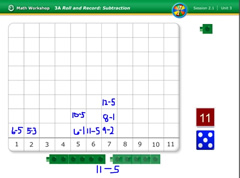
Part 1: Subtraction Roll and Record
In this game, students roll a 6 to 12 number die and a 1 to 6 dot die to generate subtraction problems. They record the difference on their gameboard.
Read: Subtraction Roll and Record Directions
Read: Ongoing Assessment: Observing Students at Work
Subtraction Roll and Record
The first grade teacher in this video clip circulates as her students play Roll and Record. She checks in with two different pairs of students. Keep in mind the Ongoing Assessment for Roll and Record questions.
Notebook
As you watch this clip, consider why the teachers focused on Daniel and then later Rebecca and Elizabeth. Use your notebook to respond to the questions below.
- What do you think she learns?
- What does she need to know/do in order to assess students in this way?
- What questions do you still have about the students' understanding?
Part 2: Observing Students as They Solve a Story Problem
In this session’s Overview, you listened to a second grade teacher describe his system for informally assessing students. He spoke about watching what his students are doing, and jotting notes.
The following video clip takes place at the beginning of the year. The class is working on a set of related addition problems. As the teacher prepared for the lesson, he drew from a component in the Investigations lesson called Ongoing Assessment: Observing Students at Work to guide what to look for as he observed students at work.
Read: Ongoing Assessment: Observing Students at Work
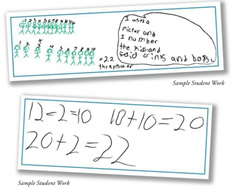
The students began by solving Problem 1:
There were 12 children playing tag on the playground.
Then 10 more children joined the game.
How many children are playing tag now?
Click on image to enlarge
The students are now working independently on Problem 2:
There were 22 children playing tag on the playground.
Then 10 more children joined the game.
How many children are playing tag now?
Did the Problem 1 help you with Problem 2?
Explain how.
The teacher walks around the classroom to observe and take notes of how students solve the problem. He stops and asks students to share how they solved Problem 2. He focuses on the last two bullets from Observing Students at Work.
Notebook
Record your observations about each student and how the teachers interact with them in your notebook. Use the Observing Students as a guide as you reflect on each student.
Observing Students as They Solve a Story Problem
Part 3: Adding Three-Digit Numbers
Mentally solve each of the following problems and record your thinking.
As you solve each of the three-digit addition problems, consider how problems such as these help you assess students as they meet one of the Common Core Gr. 3 standards for Number and Operations in Base 10: NBT.A.2.
623 + 249
930 + 377
Grade 3 – Adding Three-Digit Numbers
This teacher’s students have been working with three-digit plus three-digit problems and discussing the question: How many hundreds will there be in the answer? She knows that these three students can fluently add 3-digit numbers by place. She wants to make sure they can apply the same ideas when the sums are in the thousands. She also challenges the students to make sense of and use another strategy.
Pay special attention to the questions the teacher is asking. Think about why she is asking these questions.
Video
930 + 377 and 623 + 249
In this video clip, the teacher starts this small group session with 930 + 377 and the follows up with the problem 623 + 249.
Notebook
Record the strategies the students use. Review the questions the teacher asked. Respond to the following in your notebook.
- How did the teacher’s questions help her understand her students’ thinking?
- What did you learn about these students based on how they approached and solved the two problems?
- What could the teacher do next based on the information she gathered?
Part 4: Looking for Commonalities
Notebook
In your notebook, describe the commonalities you observed among the three teachers and students. If you want to revisit the video clips, use the links below.
Final Thoughts...
Teacher observations are an important part of ongoing assessment. Individual student observations are snapshots of that student's experience with a single activity. Over time, they provide an informative and detailed picture.
A classroom culture where students work in pairs, groups, and independently allows the teacher to observe students working in different ways. This culture must be established at the beginning of the year.
Points to consider when making observations:
- Do the math and think about strategies that may come up ahead of time – this is key to making sense of what students understand and what they don’t yet understand
- Classroom management – students working independently, no interruptions – allows you to observe them
- Observations are a time for understanding; not for teaching
- Decide on 4 or 5 students to observe and make a note about each one; do this repeatedly over the week to get a picture of your whole class
- Not sure what to ask? Start with, “How did you know?” or “What was your first step?”
From the Field
Start With Learning Targets
The foundation of a formative classroom must be learning targets in learning progressions. Any formative assessment can inform teacher and student where the student is now so both can know what comes next in the learning.
My recommended starting place is learning targets. Remember, we want learners to know where they are headed from the very beginning of the learning. Just start instruction with student-friendly versions of the target and watch what happens. Students can hit any target they can see and that holds still for them.”
Conversation between two teachers:
Teacher A Shares
“Since the students I have are Gifted/Enrichment, I informally assess (clipboard cruising, create a similar problem with the same contextual elements as what was discussed or learned in class, etc..). I also use Socratic Round Table with these kids every week so all students are able to express their thoughts and where they believe they are at with their learning. Students gain ownership, a sense of value and the ability to share their thoughts on a level playing field.”
Teacher B Replies
“I found myself wondering how I would apply this for my lower level and non-verbal students. I have really worked on having students reflect on their thinking recently and the idea of a Socratic Round Table was very intriguing, despite the fact that not all of my students are verbal. We tried this after a math lesson one day and I provided picture symbols and voice output devices for the students that needed the support. It was fascinating to see what my students could share when given the time and appropriate materials.”
from Discussion Forum Implementing Investigations online course
Activity 2: Watching and Listening to Students at Work
In this activity, you will experience two first grade experiences, both are focused on adding by groups.
- In the first experience will watch students as they share their work and consider what you learned from the students’ verbal descriptions.
- In the second experience, you will match a set of student work with written descriptions of what the students did and said as they organized a set of squares. After you match the students with their work, you will pair students based on what you’ve learned.
First Grade Students Share Their Work
To fully understand what students know, you have to listen, observe them in action, and ask clarifying questions to help them justify their thinking. Written artifacts alone tell only part of the story. Watch these first grade students as they share their work. Pay attention to what they have recorded and what they share verbally. They are solving the problem:
I see 4 people and 2 cats.
How many legs?
Notebook
Pause after watching each student.
In your notebook, describe what you learned about each student’s strategy and understanding of adding groups. Did the student’s verbal description help?
The teacher chose the students for a reason before the whole group met. He thought about the order of the student presentations. Describe why you think he chose this order?
Video
How Many Squares?
The following set of student work is from a counting problem, How Many Squares? In this activity students are asked to organize and count paper squares organized in groups of 5’s, 2’s and 1’s.
Use the virtual groups of squares to organize and count the squares. When you drag the squares you will see that there's a handle. That handle allows you to rotate them.
Notebook
Record how you counted them in your notebook. Then think about other ways the squares could be organized.
Matching Work with Student Descriptions
The work in the next two experiences represents a range of approaches in a 1st grade classroom.
- Read what the students did and said as the teacher observed them.
- Match each description with the student work.
- What, if any, new information did you glean from the descriptions?
You may proceed to this activity via the links below.
Note: You may want to print out the How Many Squares Student Work and Descriptions pdf to use as you complete this activity
Next steps...
Use what you learned from matching the student work to pair students. Explain how the partnerships could deepen the students’ understandings about organizing and finding a total number of objects.
Click here to begin.
Go to the sort Forum to share who you paired together and your reasons why.
Final thoughts…
The information from the written work without observing students as they work shows only part of students’ understandings and misunderstandings.
From the Field
If you can both listen to children and accept their answers not as things to just be judged right or wrong but as pieces of information which may reveal what the child is thinking, you will have taken a giant step toward becoming a master teacher, rather than merely a disseminator of information.”
Activity 3: Looking at Student Work Using a Rubric
Find the Product of Two 2-Digit Numbers
The following multiplication problem is part of an End-of-Unit Assessment in Investigations. Students have engaged in similar work throughout the unit. The Math Focal Points of the class work are solving 2-digit by 2-digit multiplication problems, breaking up multiplication problems efficiently, multiplying fluently by multiples of 10 and using clear and concise notation. For this assessment, students work independently to solve this problem.
The goal of all math teaching and learning is to promote a deep understanding of mathematics and develop mathematically proficient students who can think, reason, model and solve problems.”
Solve 57 x 83
Read: Multiplication Strategies
Solve 57 x 83 using two or more strategies you read about in the reading, Multiplication Strategies.
Benchmark: Students solve multiplication problems efficiently
Create a Rubric
Create a rubric
You will categorize the Levels of Understanding Descriptions for solving 57 x 83 : Meets the Benchmark, Partially Meets the Benchmark, Does Not Meet the Benchmark
Which statements describe:
- Understanding
- Accuracy
- Strategy
- Communication
Record the descriptions in the corresponding box on the blank Rubric Table.
Student Work Sort
You will look at seven pieces of student work for 57 x 83 and decide if the student meets, partially meets or does not meet the benchmark.
Read DIET protocol
This protocol helps teachers look closely at their students’ work before determining their levels of understanding for Understanding, Accuracy, Strategy and Communication.
In this sorting activity you will review the student work samples and drag each one into the corresponding bin: meets, partially meets, does not meet the benchmark.
For each piece of student work, you will:
- Use the DIET protocol to examine the student work.
- Use the rubric you created to determine whether each student meets, partially meets, or does not meet the benchmark for understanding, accuracy, strategy, and communication.
- Justify your decision
Note: It’s possible that students will meet the expectations in one category and partially meet or not meet the benchmark in another. For example a student:
Example: The results for one student might look like…
| Category | Description | Level of Understanding | Evidence |
|---|---|---|---|
| Understanding: | Clearly understood the problem | Meets | This is the place where you would indicate what part of the students work you used to decide the level of understanding. |
| Accuracy: | made a calculation mistake when adding the subproducts | Partially meets | |
| Strategy: | Broke the problem in manageable parts | Meets | |
| Strategy: | Information was disorganized and difficult to follow | Does not meet |
DIET Protocol
Students communicate their thinking through verbal descriptions, demonstrations with tools, written work and a combination of all three.
Notebook
In your notebook, describe how the rubric helped you look at the student work.
Sam and Charlie
Record your response to the following questions in relation to your Sam and/or Charlie in your Sam and Charlie Journal.
- When assessing Sam and/or Charlie, what are you hearing?
- How is what you’re hearing informing what you do to support his/their learning?
From the Field
Another form of assessment is one-on-one assessments with students. Here are examples from the field.
Kathy Richardson is one of the nation’s leading educators of elementary mathematics. She has developed a collection of assessment called Assessing Math Concepts. Her assessments span from PreK to third grade. You can view more student interviews here. Watch a several examples below.
Assessing Math Concept Examples
Assessing Math Concepts digital assessments: Didax Educational Resources
Doug Clark, a professor at Australia Catholic University, developed individual assessments students math understanding. Watch as Doug interviews students’ understanding of counting in groups and multiplication ideas.
How Many Tennis Balls and Array Dots
Discussion
Share two things about assessment for learning you are taking away from this session. Be specific.
- Remember to participate in and return to the Discussion Forum conversations you and other participants have initiated.
Notebook
Complete the Session 3 Notebook page using the indicated prompts.
In the final field of your notebook, reflect on the key take-aways from this session for your own learning and record ideas that you will implement to support math learning.
Key Learnings
Assessment for learning involves:
- checking to see what has been learned and what needs to be learned next
- engaging students in assessing their learning and the learning of others
- setting transparent kid friendly learning targets for students
- knowing the learning paths and the critical learning targets along the way depending on their needs
In order for productive assessment to be an integral part of student learning and instructional planning, teachers need to:
- create a classroom culture where assessment is a natural part of learning
- know the math and how it’s presented to the students at different grade levels
- figure out what students understand so you can plan appropriate next steps
- scaffold instruction and discussions to make them accessible to all
- plan guided group instruction with a targeted goal for all students
- ask questions that probe students’ thinking
- listen to students’ reasoning as they work
- notice what students do and how they communicate their ideas
- believe assessment is an ongoing process rather than an event