Overview
Session Focus
This session focuses on instructional strategies to support the range of learners. This range can include students who need support or excel in certain areas of mathematics (but perhaps not in others), students who are multilingual learners, and students who have particular learning needs.
Differentiation with respect to classroom instruction is a term that can hold a variety of meanings. This session will focus on adapting the math curriculum within the classroom setting during the designated math class, by the classroom teacher(s).
Important Assumptions About Teaching and Learning Mathematics
We believe that…
- All students have mathematical ideas and can be mathematical thinkers. This includes students who might not be given access to certain types of learning opportunities because someone has made assumptions about who they are and how they learn.
- All students should be engaged and supported in making sense of and understanding mathematics.
- Developing students' agency and identity as math learners is foundational to differentiating instruction.
Agency and Identity
Mathematical Identity |
Mathematical Agency |
|---|---|
|
|
|
Identity and agency are very interconnected; identity is how students see themselves as learners and agency is how students see themselves as having some sort of power to make choices and decisions about, and take responsibility for, how they interact with learning.
Reflect on the ways you currently support the range of learners in your work. What has worked well? What are some of the challenges you face? What might you like to learn more about? Briefly share a success, a challenge, and a question you have about differentiation on the Overview Forum. As you reflect, please remember one of our norms for this course: Use asset-based language when discussing students. Avoid using labels such as “low”, “high”, etc.
Activity 1: Instructional Strategies for Differentiation
This activity explores 8 instructional strategies for differentiation. Some of these strategies focus on the learning environment, while others relate to the task or problem, or the materials and tools available to students. Central to all of these instructional strategies is the assumption that identifying the main math ideas that underlie a task or problem, and observing students at work, forms the basis for making decisions about how, when, and if it makes sense to differentiate instruction.
The 8 Strategies for Differentiation
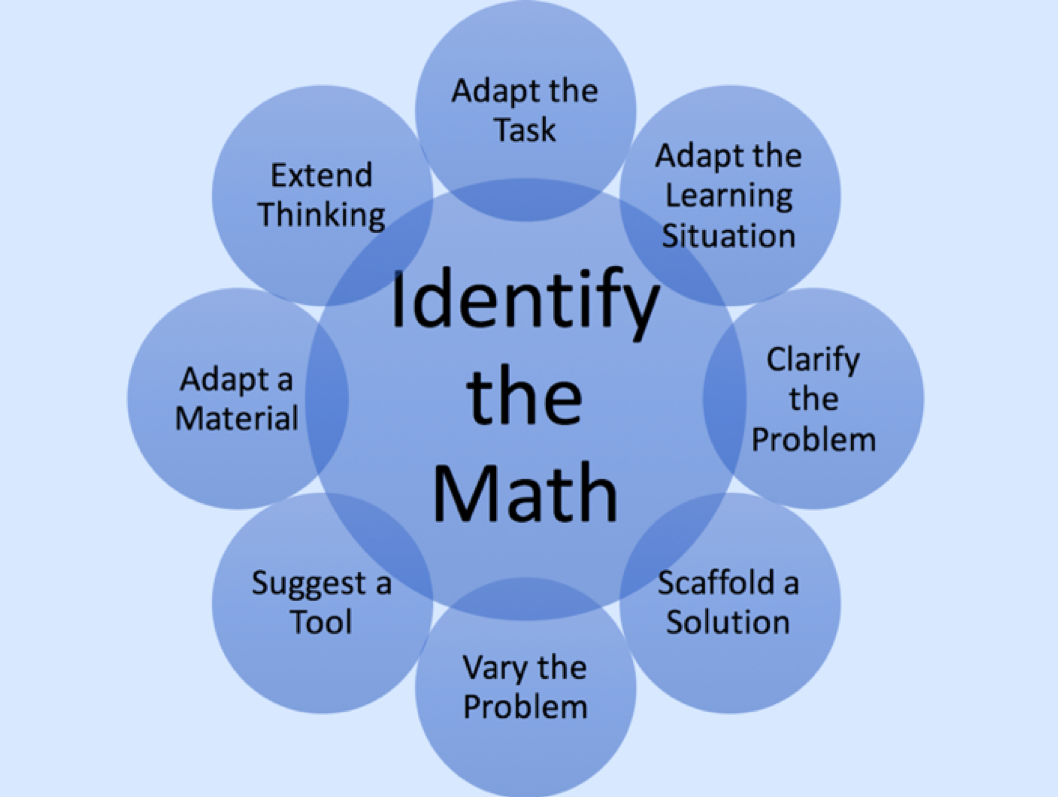
Read about the 8 Instructional Strategies for Differentiation pictured in the image above. Since these strategies will be referred to throughout the session, we highly recommend downloading this reading and printing it out for easy access in later activities.
Which of these strategies do you currently use in your work with students?
Identifying the Math and Observing Students at Work
Identifying the main math idea of an activity and observing and interacting with students as they are engaged in that activity, forms the basis for making decisions not only about how to differentiate but if and when to differentiate.
The work of this session centers around two activities—one from a fifth-grade classroom, and the other from a first-grade classroom. You will select one grade level to focus on throughout the session and read about the activity from that grade. You will also do the activity yourself, identify the mathematics, and consider how students might approach it.
Choose whether you would like to focus on the first-grade, or fifth-grade activity. You may wish to engage with both activities, but you are only required to complete one. Note that you will be returning to the activity you select throughout the session.
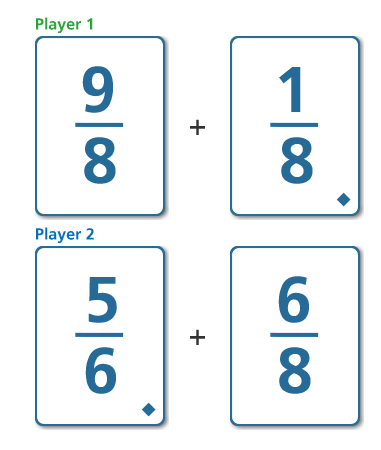
Grade 5: Addition Compare with Fractions
|
|
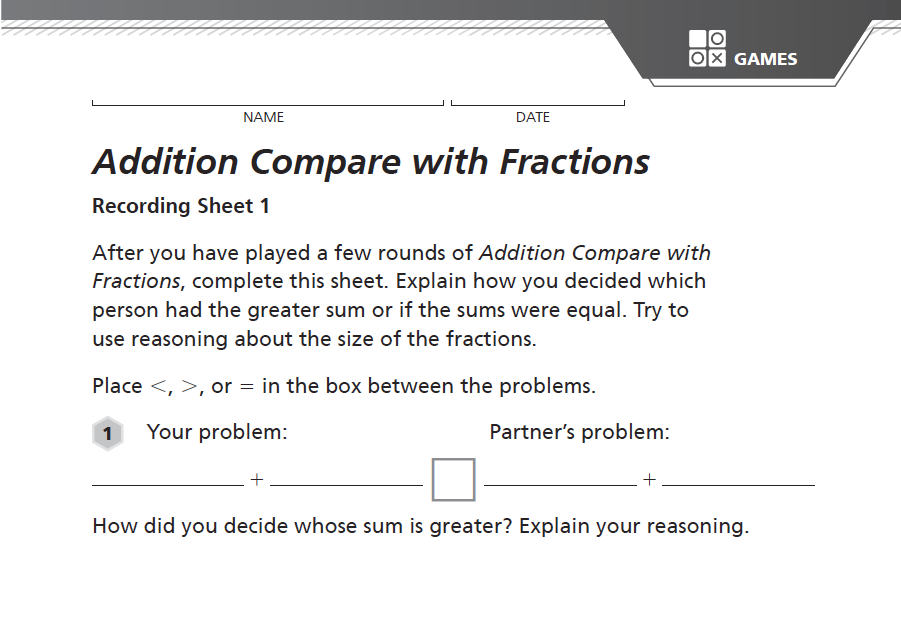 |
|---|
Which player has the larger sum? How do you know? Think about how you solved the problem, and jot down your strategy so that you can refer to it later in the session. Next, record your ideas about how students might approach this problem as well as aspects of the game that might be challenging for some students.
What important mathematics are students working on as they play this game?
Click here to read the math focus points for this game.
Watch 5th grade students playing and discussing this game. As you watch, think about the students’ strategies. How do they compare with your strategy and the strategies you anticipated that students would use? What, if anything, appears challenging for the students in the video?
Grade 1: A Story Problem about Crayons
 |
|---|
Watch as first grade teacher Cheyenne Richardson introduces this problem to students in her class.
Solve the problem. Consider the approaches that first-grade students might use to solve this problem, and which aspects of the problem might be challenging for them. Record your ideas.
What important mathematics are students working on as they solve this problem?
Click here to read the math focus points for this activity.
Look through the set of student work for this activity. As you review each student’s solution, make notes about how each appeared to approach/solve the problem.
What do students appear to understand about this problem? What challenges are students encountering?
Activity 2: Instructional Strategies to Scaffold Learning
This activity focuses on using instructional strategies to scaffold student learning. You will consider how several of the 8 instructional strategies can be used to differentiate activities for students who might benefit from more support. You will also think about how to differentiate math learning in ways that maintain the mathematical focus of a problem for all learners and create opportunities for students to become agents of their own learning.
Grade 1: A Story Problem about Crayons
The following video illustrates several ways that a teacher could differentiate the “Ten Crayons in All” activity for students who need more support.
Look through the set of student work for this activity again. Select 2-3 pieces of work and do the following:
- Describe what you see and what you notice about each piece of work.
- Think about what the next step for this student might be, remembering that it might be appropriate to do nothing at this point. Consider the suggestions in the video above or, if you prefer, another strategy and give an example of what you might do with the student. In what way does this support student agency?
Grade 5: Addition Compare with Fractions
The following video illustrates several ways that a teacher could differentiate the 5th grade game “Addition Compare with Fractions” for students who need more support.
How do the strategies in the video above maintain the mathematical focus and cognitive demand of the original activity? In what way does the next step you envision for the student support that student's agency?
Activity 3: Instructional Strategies to Extend Learning
This activity focuses on using instructional strategies to extend learning. You will consider how several of the 8 instructional strategies can be used to differentiate activities for students who are ready for more challenge and extend learning for students who need more support.
Grade 1: A Story Problem about Crayons
Watch as 1st grade teacher Cheyenne Richardson offers an extension to a student during the 10 Crayons in All activity.
What differentiation strategy does Ms. Richardson use in this video clip? How might this strategy help this student continue to engage deeply with the mathematics in this activity?
Below is an example of student work from this extension activity. Notice how the student initially starts out with a random, guess and check approach and then moves to an ordered list.
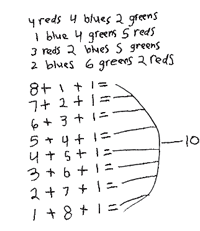
Think about the Extend Thinking Instructional Strategy as you look at the student work pictured below.

What does this student understand about addition? What idea(s) about addition is this student working on? In what way did the teacher’s question extend the student’s thinking?
Grade 5: Addition Compare with Fractions
Below are some ways that a teacher could extend the learning in this game.
Adapt the task
One way a teacher can differentiate for students who need more challenge is to Adapt the Task and have them play with 3 cards.
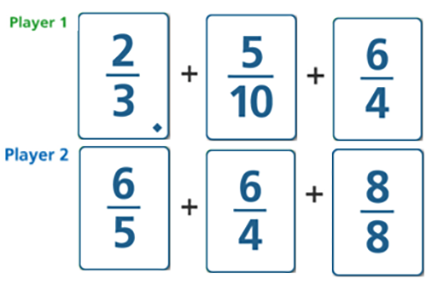
Which player has the larger sum? How do you know?
Look back to the strategy you used in Activity 1, when solving a similar problem with 2 pairs of cards; did you use the same strategy when the problem involved three cards?
Adapt the Materials & Vary the Problem
Asking students to not only determine who has more but also how much more adds another level of challenge for students. In order to make the extension reasonable, first ask students to adjust the deck and play with related fractions.
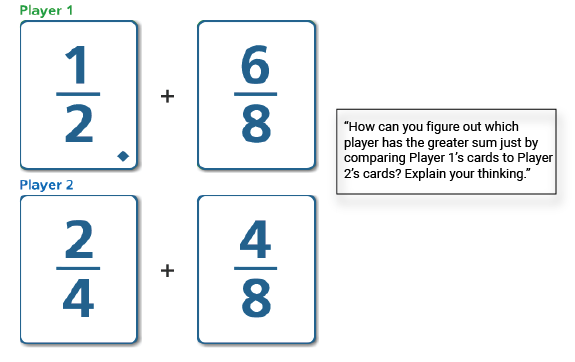
Extend Thinking
Teachers can extend student thinking by posing a problem that uses the game context but engages students in thinking more deeply about some aspect of the mathematics. For example, using the same set of cards as above the teacher might present the following problem:

In this example, the teacher would be supporting students in thinking more deeply about comparing fractions as well as asking them to explain and justify their thinking with a representation.
Extending the Thinking of Students Who Need More Support
It is important to also offer students who may typically need more support opportunities to think about a task in ways that will extend their thinking about the mathematics. For example, students who are playing with an adapted deck of cards, consisting only of related fractions less than 1, can be challenged to reason about the greater sum with a problem such as the following:
Think about a student you know or have worked with in the past. How do they see themselves as math learners? In what ways could the ideas in this session help you support that student becoming agents of their own learning? Share your thoughts on the Student Math Identity Forum.
Forums
- Return to the Overview Forum. Look through others' responses and respond to at least one post that interests you.
- Return to the Student Math Identity Forum and read everyone's posts. Respond to at least one post of interest.
Readings
Aguirre, J., Mayfield-Ingram, K., & Martin, D. (2013). The impact of identity in K-8 mathematics: Rethinking equity-based practices. The National Council of Teachers of Mathematics.
TERC. Investigations in Number, Data, and Space®: Number Games and Crayon Problems, 3rd ed. Northbrook, IL: Savvas Learning Company LLC, 2017
TERC. Investigations in Number, Data, and Space®: Rectangles, Clocks, and Tracks, 3rd ed. Northbrook, IL: Savvas Learning Company LLC, 2017
Key Takeaways
- Decisions about how to differentiate need to be made within the context of the mathematics and based on observations and interactions with students as they engage in the activity.
- Differentiation strategies should be used to support all students in making sense of important mathematical ideas and relationships. The 8 strategies for differentiation are designed to offer students multiple entry points and allow students with varying mathematical skills to engage in rigorous mathematics.
- It is important to provide students who typically need support with opportunities to extend their thinking and reason about mathematical ideas.
Please contact TERC to report any broken links or other problems with this page.