Session Summary

 This session focuses on different ways to compare and order fractions, using landmarks (0, 12, and 1), reasoning and conjectures, and a variety of models and representations.

Comparing Fractions

 Compare the following fractions without finding common denominators. Which is greater?

14 and 35

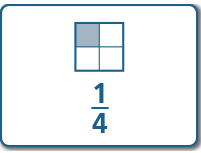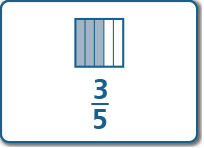56 and 78

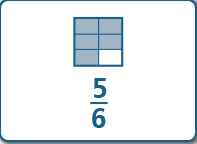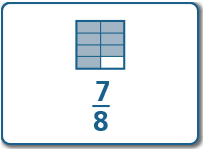How did the fraction card representations help you to make the comparisons? What other reasoning did you use?

Watch Investigations author Keith Cochran discuss how students using Investigations compare fractions using number relationships and reasoning.

What do you think students “reasoning about fractions the same way they reason about whole numbers” means? What does “number sense” with fractions look like? For you? For your students?

Below is a list of materials you will need for each activity in this session. You will also find these materials listed at point of use in the session. Pencil and paper (or computer) are needed for each activity.

Activity 1

• Fraction Cards (made in Session 2)

Activity 2

• Grade 4 SAB p. 375 Fractions in Containers

Activity 3

• Grade 5 Fraction Tracks
• Ruler or straight edge
• Directions for In-Between

In this activity you will use the Fraction Cards you made in Session 2, play a 4^th Grade game, and view a classroom video to consider ways fractions can be compared and ordered using number sense and reasoning. You will also consider generalizations that can be used to compare fractions.

Students in Grades 3-5 compare fractions and reason about their sizes, using both area (rectangles) and linear (number line) models to explain how they know which fraction is greater or if the fractions are equivalent.

Capture Fractions

Capture Fractions is a game played in 4^th grade. Students each turn over a fraction card and determine which fraction is greater. The player with the greatest fraction takes both cards. Students have played a variety of different “Capture” games since Kindergarten.

Watch how this teacher introduces “Capture Fractions” to her class. Listen to how different students explain how they know which fraction is greater. As you watch, think about what strategies students are using as they compare fractions.

How are students using the fraction cards to compare, and reason about, fractions?

Play Capture Fractions with a partner or on your own. As you play the game, think about how you determine which fraction is greater.

Which fractions were easy to compare? Why? Which fractions were hard to compare? Why?

Ordering Fraction Cards

Students in 4th grade also work on ordering fractions by placing the fraction cards they create on a number line.

Make a long number line and place the cards you made in Session 2 for 0, 12, 1 and 2 on the number line as shown below.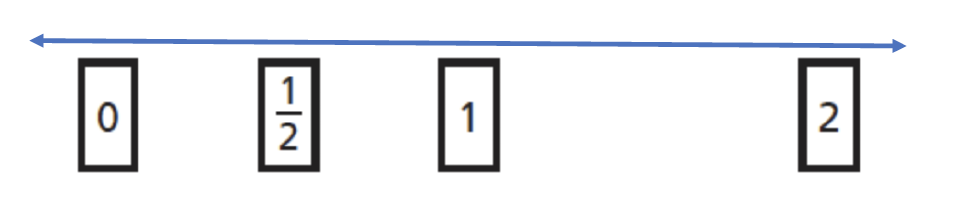

Place the remaining cards you made on the number line so that the fractions are in order, and in the approximate place they belong on the number line.

Which fractions are equivalent to the landmark (0, 12, 1, 2) numbers? How do you know?

How did you decide where to place the other fractions on your number line?

Which fractions were easy to place? Which fractions were challenging? Why?

As students' repertoire of fractions increases, they use their own mental images of fractions and their knowledge of fraction equivalencies and relationships to compare and order fractions. For example, when reasoning that 58 is more than 12, they may call upon the fact that 48 is equivalent to 12 and 58 is greater than 48. (They most likely will do this almost automatically- from their experiences with discussing the relationship between halves, fourths, and eighths.)

Making Conjectures/Generalizations

Throughout their work with operations with whole numbers, students have been making and using generalizations about numbers and the operations which they then use to help them solve computation problems. (Example of a generalization: you can change the order of the factors in a multiplication problem and the product will be the same.)

In Investigations, there are opportunities for students at all grade levels to verbalize and discuss conjectures and make generalizations about relationships and patterns that they notice. For each generalization, they are asked to consider whether:

• the generalization is always true
• it works for all numbers
• how they know it works for all numbers

This work with making conjectures (a mathematical statement that has yet to be proved) and using generalizations continues as they work with rational numbers. When students compare fractions, they use what they know about fractions and the relationship between the numerator and denominator as well as mental images of fractions. Students begin making generalizations, based on their conjectures, and use these generalizations to compare fractions.

The following is an example of a generalization for comparing fractions: If the numerator is exactly one half the denominator, then the fraction is equivalent to 12.

Read the 4^th grade Dialogue Box, Conjectures about Fractions to learn how a discussion about using conjectures to compare fractions played out in one 4^th grade classroom. As you read the Dialogue Box, think about how it supports teachers in better understanding the purpose, and the mathematics, of the activity.

Think about how you decided where to place your fraction cards on the number line. What conjectures (as described in the Dialogue Box) did you use? Which of these ideas were new to you?

Challenge:

Place the following fractions on your number line.

59

89

47

67

1320

3322

How did you decide where to place each of these fractions? Did you use generalizations or strategies you hadn’t tried before? Which ones?

In this activity, you will use landmarks (0, 12, 1), view classroom video, and examine student work to consider ways 4th graders compare fractions.

Fractions in Containers

As students work with whole numbers, they begin identifying landmarks they find useful to help them determine the magnitude of numbers (e.g. 789 is closer to 800 or 1,000 than it is to 500 or 700) and to solve computation problems (789 + 425 should be slightly greater than 1,200). In Investigations students also use landmark numbers when working with fractions. Students use the landmarks of 0, 12, 1 to help them as they compare and order fractions.

Complete the 4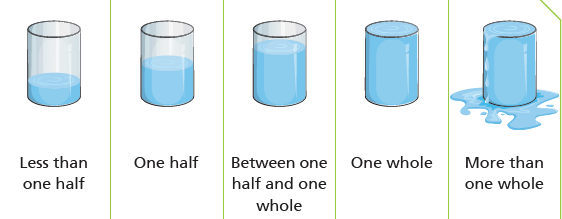th grade activity Fractions in Containers. In this activity, you will determine the relationship of each of the fractions to 12 and 1. As you’re sorting the fractions, think about what you know about each fraction, and the relationship between the numerator and denominator, that helps you decide where to write the fraction.

How did you use fraction equivalencies and other fraction relationships to sort the fractions?

What conjectures or generalizations did you use?

Which fractions were most challenging?

How did you know where to place 37?

As you watch these two video clips from a 4th grade classroom, think about these questions from the Observing Students at Work feature of Investigations.

As you watch the video, consider the first two questions shown in the Ongoing Assessment.

What did you learn about how students are using landmarks to sort the fractions?

Are there any questions (shown in blue font) you’d want to ask these students? Why?

As you view the second clip, continue thinking about the questions listed in the Ongoing Assessment. Also consider the teacher’s role in her interactions with the students.

What moves did the teacher make to guide the conversation without directing or correcting the students?

In what ways did her facilitation moves impact the small group discussion?

Lens on Equity

Classroom culture is a key element to students developing a strong sense of agency and positive mathematical identities. “Reflective teaching practice that is committed to equity will include. . . classroom cultures that encourage students to exercise their positive mathematical agency individually and collectively. These forms of agency can contribute to students developing positive identity-related stories and behaviors that affirm and demonstrate these identities." (p. 17) (Aguirre, Mayfield-Ingram, & Martin, 2013). 

• How does the teacher in the video offer meaningful feedback that draws students’ attention to making sense of the mathematics?


• How does the teacher help students move their own thinking forward?


• Think about both the actions of the students and the teacher. What evidence do you see of a “classroom culture that encourages students to exercise their positive mathematical agency individually and collectively"?


• What do you already do in your classroom to develop and strengthen this type of classroom culture? What else could you do?

Looking at Student Work

Students use their mental images of fraction equivalencies and the relationships between fractions and to landmarks such as 12 or 1 to determine which of two fractions is greater.

Look at the following pieces of student work from 4^th grade for comparing fractions. In this assessment activity, students are asked to compare 23 and 56 and explain how they knew which fraction is greater.

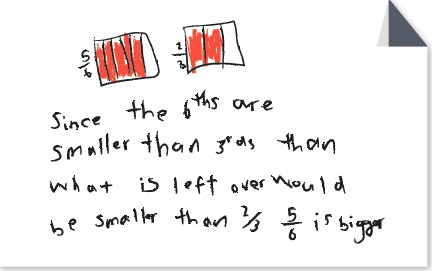
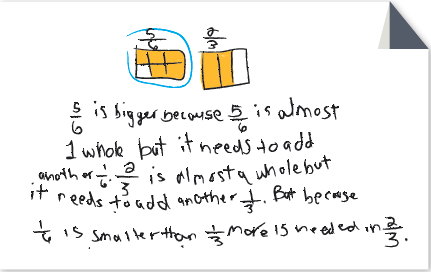
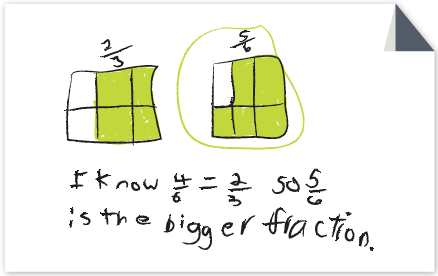
Consider:

Are students using reasoning about how close (or far) a fraction is to a landmark to decide which fraction is greater? Are they using their knowledge of equivalent fractions?

How do their words and representations show their thinking?

In this activity you will order fractions by placing them on a set of number lines; play a 5th grade game about ordering fractions and view a video of students playing this game; and consider how students use reasoning to compare and order fractions.

Fraction Tracks

Grade 5 students build on the work they did in 3^rd grade and 4^th grade with comparing and ordering fractions, but they now work with more difficult comparisons, including fractions with any denominator. (Work in 3^rd grade is limited to halves, thirds, fourths, sixths, and eighths. Work in 4^th grade is limited to halves, thirds, fourths, fifths, sixths, eighths, tenths, hundredths.) Grade 5 students continue working with these familiar fractions and gain more experience with fractions greater than 1 and their equivalents, such as realizing 96 = 112 .

Fraction Tracks are a set of seven parallel number lines that show the relationships between fractions with denominators of 2, 3, 4, 5, 6, 8, and 10. In Grade 5, students are given a set of Fraction Tracks that is incomplete and asked to finish marking and labeling the tracks to make a board for Fraction Track (a game you will play in Session 4).

Complete each of the number lines on Fraction Tracks.

Mark and label all the possible fractions (with whole number numerators) on each fraction track. Some of the fractions on each track are already marked; you will need to draw dots to mark the location of any missing fractions. Each fraction on a track should have the same denominator. (e.g. 14 , 24 , 34 , 44 ).

You may want to use a ruler to help you line up the dots on different tracks.

Feature-Math Notes

Math Notes are one type of sidebar found in Investigations sessions. Along with the Mathematics in this Unit, Teacher Notes, etc., these Math Notes provide additional information on the mathematical content at “point of use” in sessions.

Read these two Math Notes from Grade 5, Unit 3 about mathematical ideas the Fraction Tracks can highlight.

Read the 5^th grade Dialogue Box, Equivalents on the Fraction Tracks to learn what a discussion about placing fractions on Fraction Tracks looked like in one Grade 5 classroom.

What does marking and labeling fractions on the Fraction Tracks highlight about fractions and about comparing and ordering fractions? What did the students in the Dialogue Box notice about fractions and ordering fractions as they marked and labeled these number lines?

In Between Game

In Grade 5, students play In Between, a game that focuses on ordering fractions and justifying their order through reasoning about fraction equivalencies. In this game, students strategically decide where to place their fractions based on their understanding of the order and magnitude of fractions.

Carefully read the directions to In Between. A critical rule of the game is a player may not place a card between two cards that are already touching.

The game is introduced to students in the curriculum by demonstrating what a game between two players might look like when five of the twelve cards have been played. Look at the image below and think about which and where any of the remaining cards for Player 1 could be played, or if there are any cards that cannot be played.

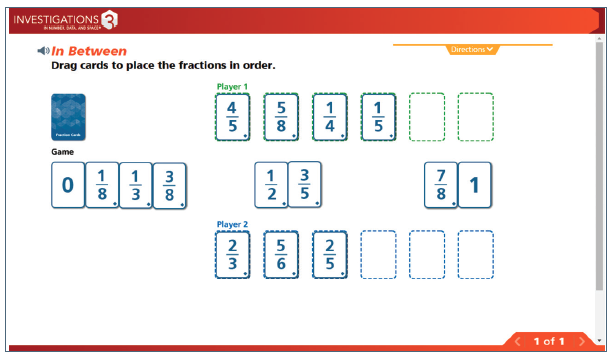
After giving time to consider which cards Player 1 might play, the teacher asks students to suggest what cards could (or couldn’t) be played and how they know. Read the suggestions made by students:

How do the student’s explanations show their understanding of fractions?

Play several rounds with a partner, or against yourself.

Consider: How did you decide where to place the cards (the order of the fractions)? What equivalent fractions or generalizations about comparing fractions were you using? What was your strategy to block the other player from using their fraction cards?

Watch this video of two 5th-graders playing In Between. As you watch, think about:

• What do these students know about fractions?
• What reasoning do the two students use to decide that 3/8 is greater than 13 ?

• What strategies are they using to compare the fractions?
• How do the students explain how “far away” 38 and 13 are from the landmark 12 ?
• How do the students explain “one-half of one-third”? Why is that important?
• What is the teacher’s role in helping the students explain their thinking?

Comparing Fractions

In this course you have used two models for fractions—area (rectangles and pattern blocks) and linear (number lines)—to understand, find equivalents, compare, and order fractions. In this session you have considered and used conjectures and generalizations to compare fractions that do not depend on finding common denominators.

Read the Teacher Note, Strategies for Comparing Fractions to consider the variety of strategies students might use to compare fractions and the reasoning behind them.

As a final activity for this session, use what you’ve learned to compare the following pairs of fractions without changing the fractions to a common denominator. Use reasoning and number relationships to explain your answer.

Show which fraction is greater using <, > or =. 

		25			13
		35			78

Post your comparison for 35 and 78 to the Comparing Fractions Forum. Then, look through the other solutions posted to the forum. Respond to at least two of your colleagues’ solutions.

Once you have completed the work in this session, go to the Session 3 Discussion Forum. Respond to one of the discussion threads in the forum, or start your own thread about a question, idea, or topic of interest that is related to the content of the session.

After you have posted your comments, take time to read others’ posts and respond to at least 2 of your colleagues.

Return to the Comparing Fractions Forum and respond to at least 2 of your colleagues posts.

• Visual models such as the fraction cards students make in Grade 4 and number lines help students compare and order fractions and make sense of equivalencies.


• Comparing fractions to landmark numbers such as 0, 12 , 1, and 2 can help students compare and order fractions.


• Students understand two fractions as equivalent if they are the same size, or the same point on a number line.


• Students move from using visual models to compare fractions to mentally visualizing fractions to compare them.


• Students use reasoning and generalizations to compare and order fractions.