Overview

Session Summary

This session focuses on how students in Investigations use contexts and representations to make sense of and solve problems that involve multiplying with fractions.

Multiplication with Fractions

When students encounter multiplication that involves fractions, they have to extend their thinking about multiplication to include fractions. Students often use the idea of multiplication as a number of groups of equal size when they multiply whole numbers. How does multiplying with fractions fit with the idea of equal groups? When students multiply whole numbers, the product is usually bigger than either of the factors (except when multiplying by 0 or 1). What is the relationship of the size of the factors to the size of the product in multiplication problems that involve fractions? Students need to build on what they know about fractions and multiplication to expand their understanding of multiplication to include fractions.

Watch Investigations author Keith Cochran talk about the importance of students making sense of multiplying with fractions and the role of context and representations.

Read the 5th grade Mathematical Practices in this Unit MP 1 essay in which a teacher asks students to think about how the problems they have been solving which include fractions are multiplication problems.

What do the students in this essay say about how multiplying with fractions is like multiplying with whole numbers? In what ways do the problems they are solving not seem like multiplication problems to them? How does working with multiplication of fractions extend students' thinking about the operation of multiplication?

Materials

Below is a list of materials you will need for each activity in this session. You will also find these materials listed at point of use in the session.

Activity 1
    None
Activity 2
    None
Activity 3

Activity 1: Multiplying a Fraction by a Whole Number

In this activity you will learn how students use skip counting on a number line to begin working on multiplying a fraction by a whole number. As you examine a video and a vignette of classroom discussions you will consider how connecting word problems and representations as well as connecting multiplication problems that involve whole numbers to problems that involve fractions can help students’ understanding of multiplying with fractions.

In fourth grade students work on multiplying a fraction by a whole number. They solve problems such as: Sabrina walks 14 mile to school every morning. How many miles would she walk to school in 5 days? Students use representations to solve problems like these and are asked to write multiplication equations to represent the problems. This work with multiplying a fraction by whole number continues in 5th grade and the focus continues to be on solving problems using representations and writing multiplication equations that match the problem.

Counting Around the Class

In 3rd and 4th grade students do a Ten-Minute Math Activity called Counting Around the Class. In this activity students count around the class by a particular number. This activity helps students connect skip counting to multiplication and connect multiplication and division equations to multiplicative situations. In 4th grade students also count around the class by fractions.

For example, students might count around the class by 26. Each student takes a turn saying a successive number—26, 46, 66, etc.– until each student in the class has said a number. The teacher records the count on a number line which in the end will look something like this:

Students are asked questions such as:

  • What number did the 9th person say? How do you write 186 as a whole number or a mixed number?

  • What is a multiplication equation that would represent 9 people counting by 26?

  • What number did the 12th person say? How do you write 246 as a whole number or a mixed number?

  • What is a multiplication equation that would represent 12 people counting by 26?

In addition to answering the questions, as they count around the class by 26 students might notice:

  • The numerator of the fractions goes up by 2 each time-- 26, 46, 66

  • The numerator of the fraction the 9th person says is 9 x 2, the numerator of the fraction the 12th person is 12 x 2

  • Every 3rd person says a whole number

Draw a number line and label it with whole numbers from 0 to 3. Skip count by 38 eight times and place each fraction on the number line.

  • What number would the 5th person say? How do you write that fraction as a whole number or a mixed number?
  • What number would the 14th person would say? (This is not shown on the number line.) How do you know? How do you write that fraction as a whole number or a mixed number?
  • What multiplication equation would represent 14 people counting by 38?
  • What patterns or relationships did you notice when you skip counted by 38?

Making Sense of Multiplying a Fraction by a Whole Number

Use a representation to solve each of the following problems. Write a multiplication equation that represents each problem.

      A. Maya runs 12 of a mile each day for 12 days. How many miles does Maya run in all?
      B. K.C. runs 14 of a mile each day for 12 days. How many miles does K.C. run in all?
      C. Joey runs 34 of a mile each day for 12 days. How many miles does Joey run in all?

For each problem where in your representation do you see:

  • - the fraction (12, 14, 34)?
  • - 12 days?
  • - the number of miles the person ran altogether?
  • - the parts of your multiplication equation?

How did solving the first 2 problems help you solve the 3rd one?

In the Running Problem Forum post your representation and multiplication equation for Problem C about Joey. Then answer the following questions: Where do you see the numbers in the word problem in your representation? Where do you see the parts of your multiplication equation?

Students in a fourth grade class solved the three problems above. Jake and Harry made the following representation to solve the problem about Joey.

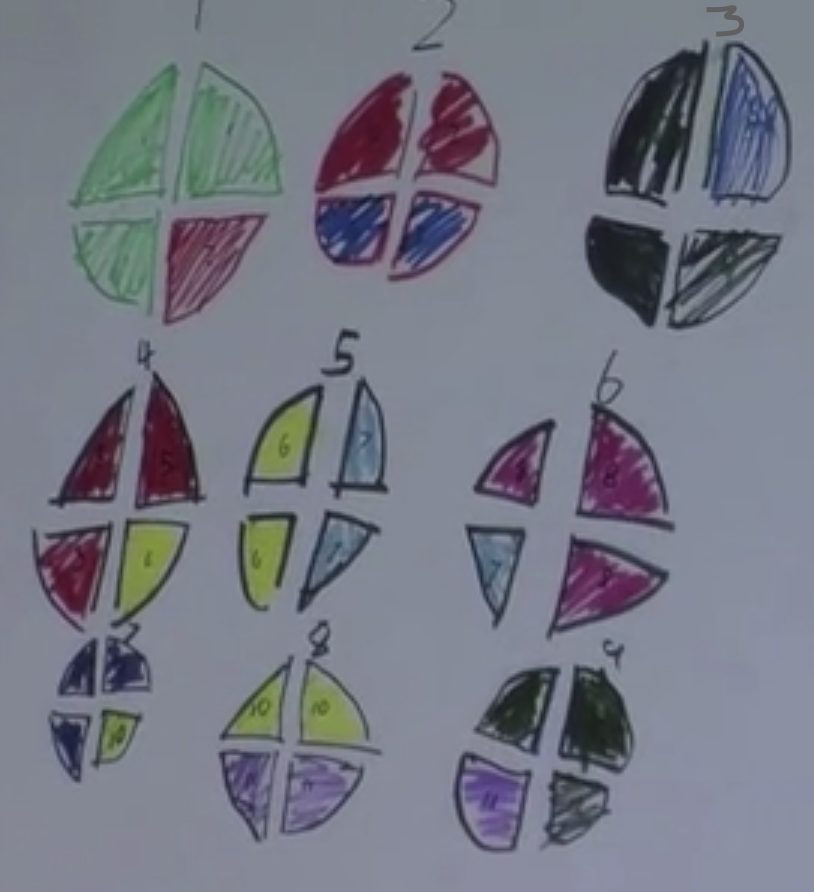
Where in their representation do you see:

  • - 34?
  • - the 12 days?
  • - the number of miles Joey ran altogether?
  • - What do you think the numbers and the colors represent?

The class then had a discussion about how they solved the three problems and the representations that were used.

In the following video the class is discussing Jake and Harry’s representation. Watch the video two times.

Video from: Russell, S. J., Schifter, D., Bastable, V., Higgins, T., Kasman, R. (2017). But Why Does It Work?: Mathematical Argument in the Elementary Classroom. Heinemann.

The first time you watch it consider:

What more did you learn about Jake and Harry’s solution from this discussion? What are the other students noticing or trying to figure out about Jake and Harry’s representation? What does this discussion highlight about the complexity of solving problems that involve multiplying a fraction by a whole number?

The second time you watch it consider:

How did the teacher’s facilitation of the discussion help students make sense of Jake and Harry’s representation? Make sense of multiplying a fraction by a whole number?

Connecting Representations, Equations and Word Problems

The emphasis in Investigations in 4th and 5th grade as students solve problems that involve multiplying a fraction by whole number is on students making sense of the problems and solving them with understanding. In discussions the teacher often asks the students to connect the word problem, the representations they make and the multiplication equations they write, which helps them expand their understanding of multiplication to include fractions.

Read the 5th grade Dialogue Box: Strategies for Multiplying a Fraction by a Whole Number in which students explain their ways of solving a problem that involves multiplying a fraction by a whole number and the teacher asks them to connect their representations to equations that represent the problem.

How did these students solve the word problem? What connections were they making between multiplication and the problem they were solving? How did the teacher facilitate students making these connections?

Lens on Equity

As Foote and Lampert write in their article, I Have a Solution to Share: Learning Through Equitable Participation in a Mathematics Classroom, “Student participation is an issue of equity and achievement; students who participate more generally learn more from the lesson, and low rates of participation can predict low achievement in the early grades (Cohen, 1984; Finn & Cox, 1992). Learning can be conceptualized as evolving participation in a set of practices (Lave & Wenger, 1991). Equity, although defined in many different ways, is fundamentally about fairness or justness (Gutiérrez, 2002); equitable participation in mathematics classrooms results in learning and therefore achievement.” (Foote and Lampert 2011, p. 247)   

Teachers’ and students’ ideas about students’ math abilities may impact, whose work is publicly shared, in what ways, and who is called on, for what type of question, as well as how comfortable a student feels participating in classroom discussions. Teachers and students alike may have implicit biases about who is a “math person” and what it means to be “good at math.” This can impact whose ideas are shared, taken up, and treated as mathematically powerful. Therefore, as Aguirre, Mayfield-Ingram and Martin write in their book, The Impact of Identity in K-8 Mathematics, “Instruction that values multiple mathematical contributions, provides multiple entry points, and promotes student participation in various ways (teams, groups, and so on) can aid the development of a student’s mathematical learning identity.” (Aguirre, Mayfield-Ingram, & Martin, 2013, pp.43) 

In the Dialogue Box you just read, in what ways do you see the teacher encouraging participation from students?   

In what ways do you support and encourage participation in discussions from your students, particularly those less likely to participate?  How do you decide who is called on or whose work is shared? In what ways do you think you can work to counteract implicit biases and further support equitable participation in discussions in your classroom? 

 

Students' understanding of multiplication as groups of groups is a helpful starting place as students work on making sense of multiplying a fraction by a whole number. While students need to move from thinking of “the number in each group” as a whole number to a fractional amount, students are usually able to incorporate this idea into their model of multiplication. For example, 3 groups of ¾ being written as 3 x 34 seems connected to equations with whole numbers such as 3 x 1 representing 3 groups of 1.

Activity 2: Multiplying a Whole Number by a Fraction

In this activity you will solve problems that involve multiplying a whole number by a fraction or a mixed number using fraction bars and consider how these problems involve multiplication.

In 5th grade students solve word problems that involve multiplying a whole number by a fraction and a whole number by a mixed number such as these: Margaret rides on a bike path that is 32 miles long. On Wednesday, Margaret biked 58 of the bike path. How many miles did she ride?

When students start working with problems that deal with a fractional amount of a whole number, it is more challenging for them to use their previous images of multiplication to make sense of these problems. Students are often able to solve problems like these but do not necessarily see them as multiplication problems.

Multiplying a Whole Number by a Fraction: Fraction Bars

In Investigations 5th grade students represent and solve problems that involve multiplying a whole number by a fraction, a whole number by a mixed number and a fraction by a fraction using fraction bars.

Consider the following problem:

John is in a bike race. The total distance he bikes is 180 miles. If he biked 16 of the distance in one day, how far did he bike?

Imagine that the length of this fraction bar represents the whole race in this problem – 180 miles.

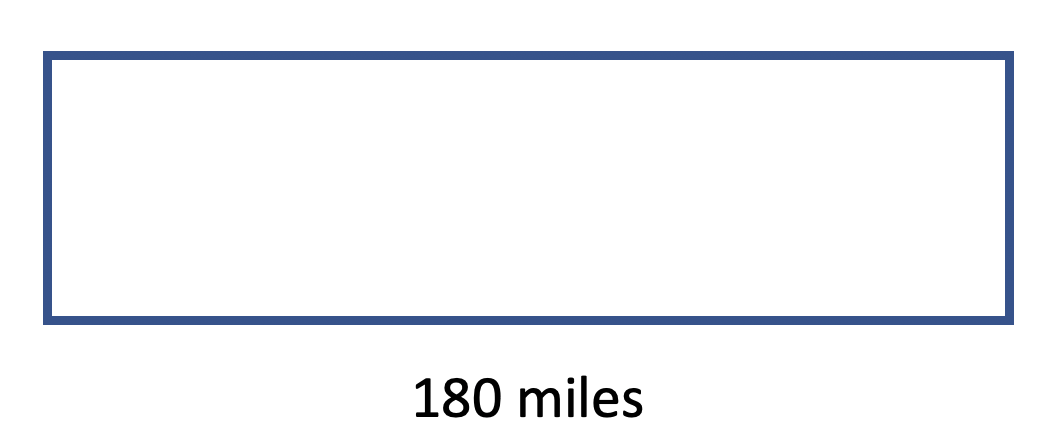
Use a fraction bar to represent and solve the problem about John’s bike race.

Where do you see 180 and 16 in your representation?  Where do you see the number of miles he raced in one day in your representation?

Watch as Grace shares her solution to this problem using the app Explain Everything.

Watch as Haley shares her solution to this problem using the app Explain Everything.

Where do you see 180, 16 and the number of miles John raced in one day in Grace’s and Haley’s solutions? What understandings did these students use to solve the problem? What connections do you see between Grace’s and Haley’s solutions and how you solved the problem?

Read the 5th grade Dialogue Box: Why Can We Write 16 of 480 as 16 x 480?  in which students are puzzling over how a similar problem can be represented with a multiplication equation.

What ideas about multiplication and fractions are the students puzzling over? How did thinking of a similar problem using whole numbers help students think about multiplying with fractions? Are there ways this discussion helped you think about multiplying a whole number by a fraction?

Watch the following video of author Keith Cochran talking about the importance of connecting contexts and representations to equations for students making sense of multiplying a whole number by a fraction.

Multiplying a Fraction and a Mixed Number

The problems discussed above involved multiplying a whole number by a unit fraction. Students in 5th grade also solve problems that involve multiplying a whole number by a non-unit fraction and multiplying a whole number by a mixed number. Most students continue to solve these problems using fraction bars.

Solve the following word problem using fraction bars or another representation. Represent the word problem with a multiplication equation.

The Astounding Race is a bicycle race that is 100 miles long. Lourdes is going to ride in the Monster Bicycle Race, which is 2 45 times as long as the Astounding Race. How long is the Monster Bicycle Race?

Consider: Where do you see the numbers in the equation in your representation? How does this problem involve multiplication?

Read the 5th grade Teacher Note: Multiplying with Fractions to learn about the complexities of students expanding their understanding of multiplication to include multiplying with fractions.

What is complex about understanding multiplication that involves fractions? How can connecting multiplying with fractions to multiplying with whole numbers help students make sense of multiplying with fractions?

Activity 3: Multiplying a Fraction by a Fraction

In this activity you will use fraction bars and arrays to solve problems that involve multiplying a fraction by a fraction.

Multiplying a Fraction by a Fraction: Fraction Bars

Students continue to use fraction bars when they are first introduced to multiply a fraction by a fraction. For example, here is a fraction bar, half of which is shaded.

Suppose we put stripes on 12 of the shaded part.

What fraction of the whole fraction bar is striped?

Solve the problems on the Student Activity Book page, Fractions of Fractions.

After you solve the problems consider: How are these problems different from multiplying a fraction and a whole number? Are there different things you have to pay attention to or make sense of?

Students use fraction bars to multiply a fraction by a fraction when at least one of the fractions is a unit fraction (a unit fraction is a fraction with a numerator of 1). However, when students are asked to multiply two fractions when neither fraction is a unit fraction, it is challenging to use a fraction bar as a visual model. Instead, students are introduced to using an array for problems that involve multiplying two fractions.

Multiplying a Fraction by a Fraction: Arrays

In Investigations students use arrays to solve multiplication problems that involve whole numbers. Arrays can also be used to solve multiplication problems that involve multiplying a fraction by a fraction. If this is a new model for you, read the 4th grade Teacher Note: Representing Multiplication With Arrays to familiarize yourself with how the array models are used for multiplication with whole numbers in Investigations. This Teacher Note also includes an example of using an array to multiply mixed numbers.

Math Words and Ideas

Watch Math Words and Ideas: Multiplying a Fraction by a Fraction to review how students multiply a fraction by a fraction using fraction bars and learn how students use an array model to multiply a fraction by a fraction. Pay particular attention to how the array model is used, as you will be using the array model to solve some problems.

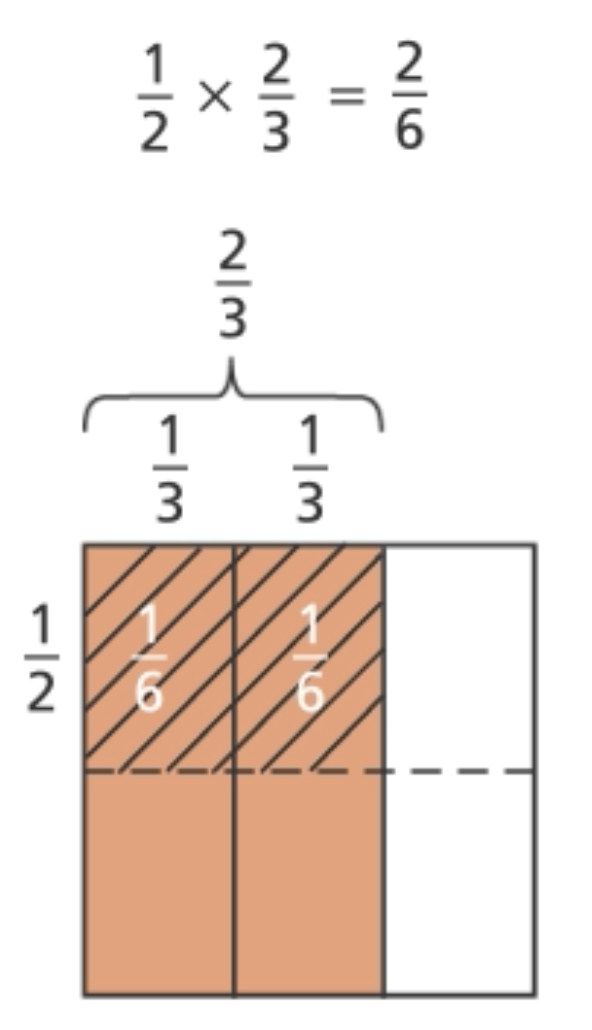Solve the problems on the Student Activity Book page, Using Arrays to Multiply Fractions by drawing an array for each one. Also write a multiplication equation for each problem.

As you solved these problems you may have realized you needed to keep track of the whole each fraction refers to. This is important for students to pay attention to as they solve problems like these as is highlighted in the following math note.

Forums

  • Once you have completed the work in this session, go to the Session 5 Discussion Forum. Respond to one of the discussion threads in the forum, or start your own thread about a question, idea, or topic of interest that is related to the content of the session.
  • After you have posted your comments, take time to read others' posts in the Session 5 Discussion Forum and respond to at least 2 of your colleagues.
  • Return to the Running Problem Forum and respond to at least 2 of your colleagues' posts by commenting on where you see the different parts of the word problem and their multiplication equation in their representation and/or by comparing their representations to the representation you used to solve the problem.

Key Learnings

  • Students build on what they know about fractions and multiplication to expand their understanding of multiplication to include fractions

  • Students use representations such as fraction bars and arrays to solve problems that involve multiplying with fractions

  • Considering similar word problems using whole numbers can help students make sense of multiplication that involves fractions

  • Connecting the numbers in word problems, representations and equations helps students make sense of multiplying with fractions

Readings

Mathematical Practices in this Unit MP1 – from Grade 5 Unit 7 Races, Arrays, and Grids.

Dialogue Box 4: Strategies for Multiplying a Fraction by a Whole Number - from Grade 4 Unit 6

Fraction Cards and Decimal Grids.

Dialogue Box 1:  Why Can We Write 16 of 480 as 16 x 480?  - from Grade 5 Unit 7 Races, Arrays, and Grids.

Teacher Note 1: Multiplying with Fractions - from Grade 5 Unit 7 Races, Arrays, and Grids. 

Teacher Note 3: Representing Multiplication with Arrays - from Grade 4 Unit 1 Arrays, Factors, and Multiplicative Comparison.  

The readings above are all published in  Investigations in Number, Data, and Space®, 3rd ed. Northbrook, IL: Savvas Learning Company, LLC, 2017.