The focus of this session is on the operations of addition and subtraction in the early grades.

You will:

• learn about the building blocks of computation
• play games that involve both counting and addition and subtraction
• learn about the story problem routine
• analyze the strategies students used in some student work
• consider how students work on addition facts in Investigations
• see how students develop and discuss generalizations about addition and subtraction

Getting Started: Solving a Story Problem

Solve the following problem. You may want to jot down your steps for solving the problem.

Click on [show] to view possible solutions to this problem.

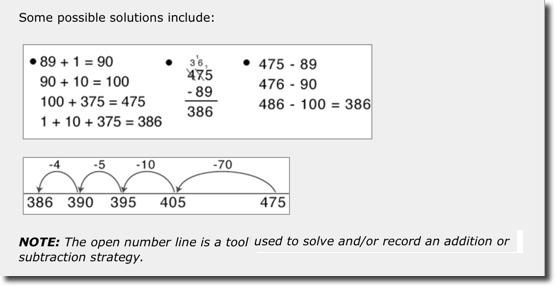
What do you need to know and understand about addition, subtraction and numbers to solve this problem using these strategies?

In this activity, you will learn about the building blocks involved in developing fluency with addition and subtraction; and play games that involve counting and addition or subtraction.

Developing Computational Fluency

A main goal in Investigations is for students to develop computational fluency - being able to accurately, efficiently and flexibly solve computation problems.

Watch Investigations authors Susan Jo Russell and Karen Economopoulos talk about computational fluency.

What aspects of computational fluency are you left thinking about?

Developing computational fluency with whole numbers is central to the elementary curriculum. This development includes the building blocks of computation.

Counting and Addition and Subtraction

In Kindergarten and toward the beginning of first grade students play a number of games that bridge counting and performing the operations of addition and subtraction. While students can play these games by counting alone, the problems they pose (e.g., How many now?) represent addition and subtraction situations. These situations represent and model the operations of addition and subtraction for young students, even if many students are counting as they play.

Play at least two of the following games:

Consider: What might students learn about addition and subtraction while playing these games?

In this activity, you will learn about the story problem routine; sort student work by the approaches students used to solve addition and subtraction problems; and write different types of addition and subtraction story problems.

Story Problem Routine

Beginning in Kindergarten, students solve story problems. This work continues throughout the grades and is an essential part of Investigations.

As students work on story problems, they focus on making sense of the action of different types of addition and subtraction problems and developing strategies to solve them.

The Story Problem Routine is used in Kindergarten, first and second grades. Students solve story problems using the following steps:

Watch the following clip of a teacher introducing a story problem to her students using the Story Problem Routine.

The Story Problem Routine offers students an opportunity to engage in Mathematical Practice 1: Make sense of problems and persevere in solving them.

As students visualize the story in their mind, and think about the quantities involved, they work to understand the context and reason about how the action of the story impacts the quantities involved.

Feature - Math Practices in the Unit Essay

The eight Mathematical Practices are a critical part of students’ mathematics learning. Each curriculum unit focuses specifically on two of the Mathematical Practices. The Mathematical Practices in This Unit essay in each unit describes each of the two highlighted Mathematical Practices in detail and provides examples from the unit of how to engage students in those practices.

Read the following Math Practices in this Unit essay from first grade for an example of how students engage in Mathematical Practice 1: Make sense of problems and persevere in solving them during the story problem routine.

Approaches to Solving Addition and Subtraction Problems

Students use a variety of approaches for solving addition and subtraction problems. In Kindergarten and first grade, their approaches are grouped into the following categories:

• counting all
• counting on or back
• counting or adding up (subtraction only)
• numerical reasoning

Read Approaches to Addition and Subtraction Problems which discusses these strategies in depth.

Student Work

‘Looking at Student Work’ (LASW) is an integral part of the work in a mathematics classroom – we assess students’ work to inform our teaching. We encourage you to use this LASW protocol as a way to make sense of students’ work.

Review the seven samples of 1st grade student work here. For each piece of student work consider:

• What strategy do you think the student used to solve the problem: Counting All, Counting On Or Back, Counting or Adding Up, or Numerical Reasoning? (You might want to refer to the Approaches to Addition and Subtraction Problems reading you read earlier in this activity.)
• What do you think the student knows and understands?
• What do you think the student does not yet understand or is still working on?

Story Problem Types

In the early grades, students solve a variety of different types of addition and subtraction problems.

Read Types of Story Problems which describes the different types of addition and subtraction problems students encounter.

Based on the reading, Types of Story Problems, choose two problem types, and create your own story problem for each type. At least one of the story problem types should be one with which you are less familiar.

In this activity, you will see how students learn addition and subtraction facts in Investigations, and how they develop and discuss generalizations about addition and subtraction.

Fluency with Addition and Subtraction Facts

Developing fluency with addition and subtraction facts is an important part of efficiently doing computation. Students work with addition and subtraction facts in a variety of games and activities in Kindergarten, first and second grade. Students are expected to be fluent with the single digit addition facts and related subtraction facts by the end of second grade. In second grade students work on sets of facts grouped in categories (doubles, near doubles, etc.). Throughout second grade there are class discussions about how to learn specific sets of facts.

Read the following:

• Addition and Subtraction Facts in Second Grade to learn more about how students work on learning addition and subtraction facts in Investigations.
• Near Doubles where students discuss using facts they know to learn facts they don’t know.

As students work on learning addition and subtraction facts students are encouraged to use facts they know to help them determine facts they don’t know.

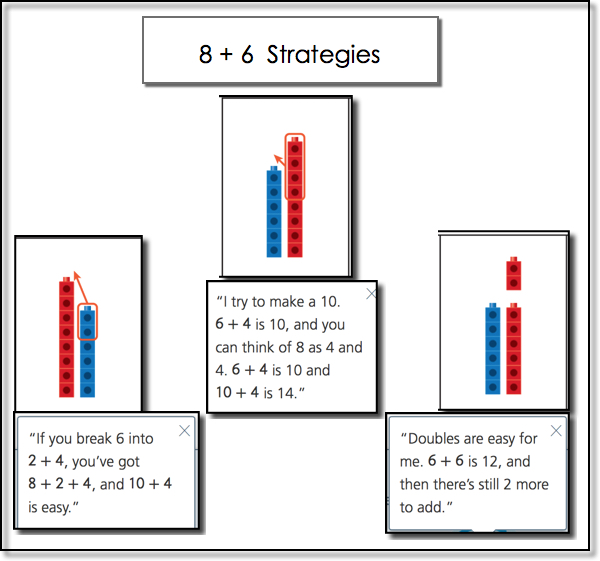
Click on [Show] to see examples of how students may use facts they know to figure out facts they don’t know.  In these examples students use cubes to illustrate how the facts are related.

Fact Cards

One of the ways students practice the addition and subtraction facts is using Fact Cards.

Students write clues using facts they already know for the facts they find difficult to remember. Click on [Show] to see example clues students might write to solve the fact 7 + 8.

What clues would you write on these fact cards to help with each of these facts?

How might using known fact clues help students learn new addition and subtraction facts?

Students engage in Mathematical Practice 7: look for and make use of structure, as students use facts they know to help them learn addition and subtraction facts they don’t know.

Generalizations

Students use what they know about numbers and about the operations of addition and subtraction as they begin to develop and use strategies to solve addition and subtraction problems.

In other words, they rely on generalizations they understand about numbers and about addition and subtraction.

The following is an example of a generalization for addition:

If you add 1 to one of the addends in an addition problem, the sum will increase by 1.

For example:

In Investigations, there are opportunities for students at all grade levels to verbalize and discuss generalizations about relationships and patterns that they notice. For each generalization, they are asked to consider whether:

• the generalization is always true
• it works for all numbers
• how they know it works for all numbers

Does Order Matter?

Watch as students develop a generalization about the order of addends in addition and the teacher asks the students to prove why it works.

Consider the following questions as you watch the video:

• What is the math that students are working on? What do they understand about addition and subtraction?
• What generalizations are students making? How are they justifying their generalizations?
• How does their cube model relate to the specific example of 23 + 2? How does the modeling go beyond the specific example?
• What is the teacher’s role in this discussion?

After watching the video share your thoughts about the video in the Does Order Matter? Video Forum.

Teachers’ questions are critical to moving students to thinking about generalizations in the mathematics they are working on.

Read Questions That Promote Thinking about Generalizations.

Once you have completed the work in this session, go to the Session 2 Discussion Forum.

What do you see as the key elements of the work students do in the early grades with addition and subtraction? How does this work support their development of computational fluency and their understanding of the operations of addition and subtraction?

Note:

• These questions are a stepping off point to start good conversations and therefore the questions are purposefully broad. There are no correct answers to the questions!
  
• If you start a thread think about what the key point or main focus is and title your post accordingly. This can help focus each conversation.

• To solve computation problems efficiently and flexibly students need to develop the building blocks of computation.
• As students work on story problems, the focus is on making sense of the action in the problems and on developing strategies that make sense to them to solve the problems.
• Young students commonly use one of four approaches to solving a story problem: counting all, counting on or back, counting or adding up, or numerical reasoning (using numbers they know).
• Students learn addition and subtraction facts in Investigations by using what they already know about numbers and number relationships and about the properties of addition and subtraction and not just simply by rote memorization.
• Students make, discuss and justify generalizations about relationships and patterns they see in the mathematical work they do.