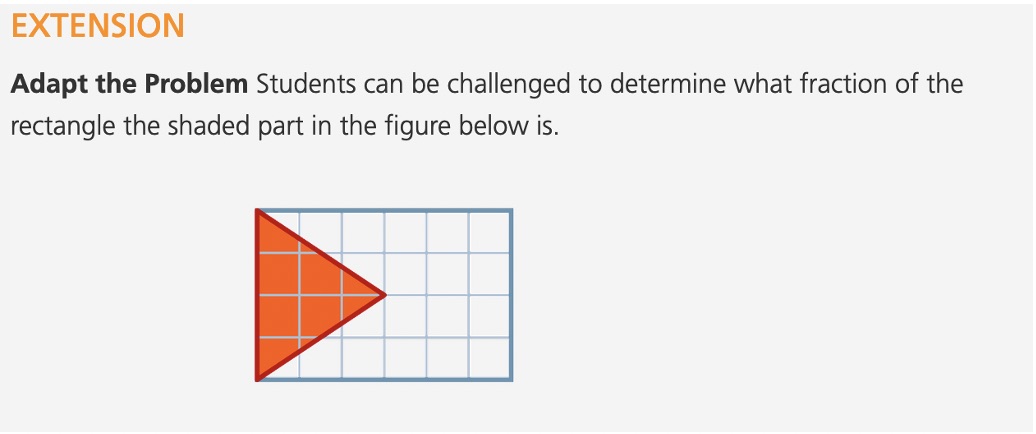
Overview
This session focuses on how students make sense of fractions, compare fractions and do computation with fractions in Investigations.
In this session, you will:
- examine the variety of representations that students use to make sense of fractions and to build their knowledge of fraction equivalencies
- compare fractions using both representations and reasoning
- estimate answers to addition and subtraction problems that involve fractions
- multiply fractions and whole numbers and learn how students expand their understanding of multiplication to include fractions.
Materials
Print:
- 4 x 6 Rectangles Sheet (Activity 1)
- Fractions in Containers (Activity 2)
- Fractions on the Number Line (Activity 2)
- Fraction Pairs to Compare (Activity 2)
- Big Bicycle Race (Activity 3)
Getting Started: Visual Representations of Fractions and Mixed Numbers
On paper, write ⅔ and 1 ¾ and sketch illustrations of each.
Next, consider the three types of representations of fractions below.
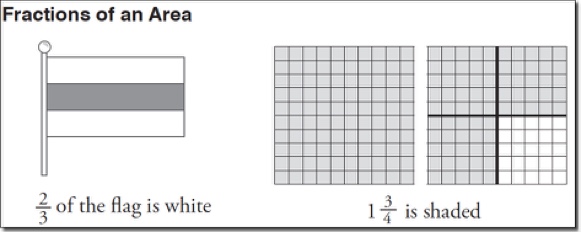
Fractions of an Area
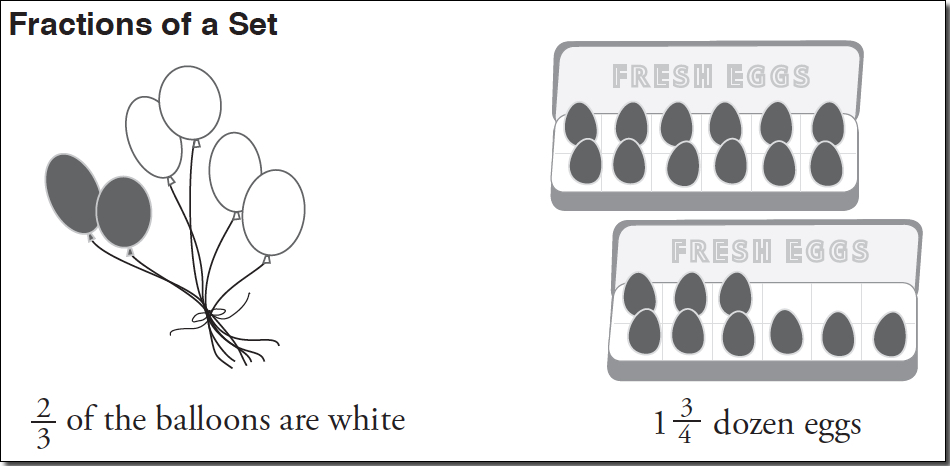
Fractions of a Set
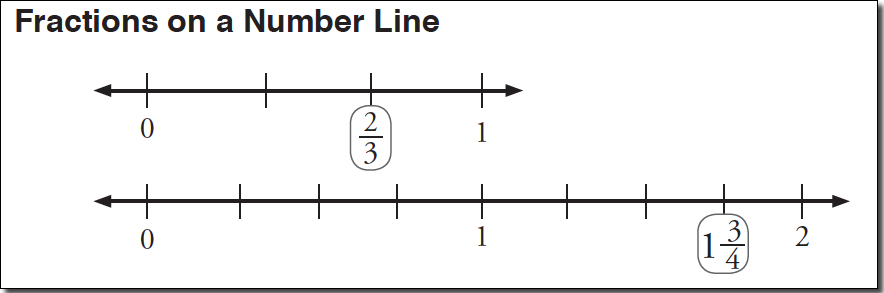
Fractions on a Number Line
How are these representations similar to or different from your illustrations?
Guess My Rule with Fractions
In fifth grade, students play a version of Guess My Rule with fractions. In this game students work on ideas about fractions using fractions of a set.
In this case, the "set" is the group of people below. You will use fractions to represent the number of people that have or do not have given characteristics.
Write down your answers to the following questions:

What fraction of the people above are…
…wearing stripes?
…wearing a jacket?
…wearing pants?
What fraction of the group are not…
…wearing stripes?
…wearing a jacket?
…wearing pants?
Next consider the larger group of people shown below. Write down your answers to the following questions:

What fraction of the people above are…
…wearing stripes?
…wearing a jacket?
…wearing pants?
How did the fractions change when the number of people in the group changed?
In Investigations, students use a variety of representations to make sense of, compare and compute with fractions.
The representations of fractions as area and as fractions of a set emphasize that:
- a fraction shows the relationship between two numbers, one representing a part (2 white stripes on the flag) and the other the amount of parts in the whole (3 equal sized stripes on the flag)
- a fraction represents a part of a whole
- the part the fraction represents is one or more equal parts
In addition, the number line representation emphasizes that a fraction is a quantity.
Activity 1: Understanding Fractions
In this activity, you will learn how students develop an understanding of fractions as parts of a whole, or several wholes, using area models; explore ways students develop an understanding of fractions as both distances and numbers as they represent fractions on a number line; and consider how students use different representations to build their knowledge of fraction equivalencies.
Developing Meaning for Fractions
Students develop meaning for fractions and a repertoire of fraction equivalencies over time. They work with different tools, models and contexts that enable them to visualize fractions as both equal parts of a whole, and as numbers.
Read Developing Meaning for Fractions to learn how students develop their understanding of fractions as both parts of a whole and as numbers.
Consider the following based on the reading:
- What are some of the challenges students face in developing meaning for fractions?
- How can drawing on prior knowledge about whole numbers be misleading for students?
- In what ways can tools, such as area models, help students construct an understanding of fractions as equal parts of a whole?
- In what ways can tools such as the number line help students construct an understanding of fractions as numbers?
Exploring Area Models for Fractions
In the primary grades, students partition familiar shapes into equal parts and consider whether equal parts of the same whole must look the same. This work supports students in developing an understanding of what fractions are and how they can be used to name quantities. Third and fourth grade students continue to work with fractions in the context of area.
As students work with pattern blocks in Kindergarten and first grade they develop a familiarity with the relationship among the pattern blocks.
For example, they may notice that two of the trapezoid pattern blocks make a hexagon pattern block, as do three rhombuses and six triangles. This knowledge lays the foundation for work with pattern blocks focused on fractions in later grades.
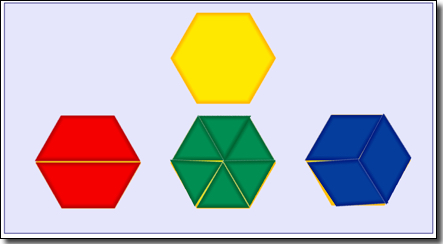
Fraction Cookies
In third grade, one of the ways pattern blocks are used as an area model for fractions is in the context of cookies. In this context, one hexagon pattern block equals one cookie. Students name fractional amounts of different pattern blocks in relationship to the hexagon pattern block. One of the games third-graders play in this context is Fraction Cookies.
- Click on the image below to play Fraction Cookies online. If possible, play with a partner.
- Follow the directions at the top of the game page. Pay special attention to steps 4 and 5.
As you play, consider how this game supports students in visualizing fractions and developing visual images of equivalent fractions.
Read Visualizing Fraction Equivalencies to learn how students use representations to build their knowledge of fraction equivalencies.
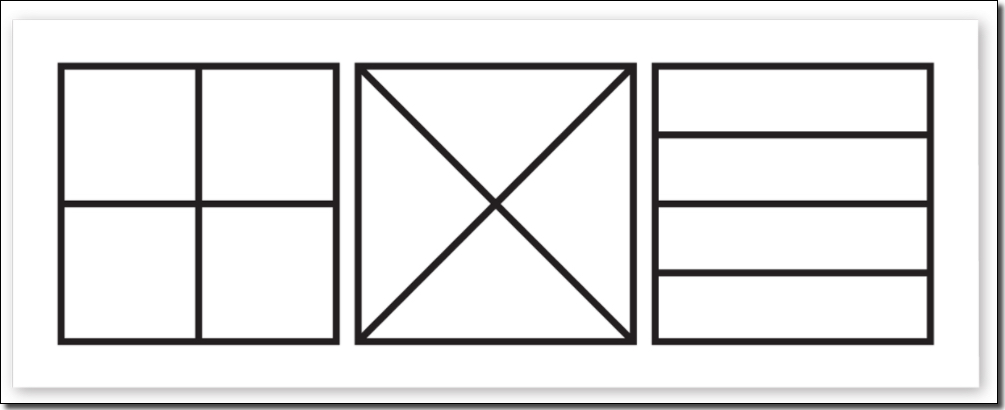
Fractions of 4 x 6 Rectangles
Fourth grade students partition 4 x 6 rectangles to represent and compare different fractional amounts. Like pattern blocks, this area model supports students in visualizing and identifying relationships between fractions, identifying equivalent fractions and explaining why they are equivalent.
- Print the 4 x 6 Rectangles sheet.
- Consider a 4 x 6 rectangle as one whole.
- Shade in the following fractional amounts: 1/4, 2/3 and 5/8.
How do you know that these shaded amounts are exactly 1/4, 2/3 and 5/8 of the whole rectangle?
How would you name the unshaded part of each rectangle?
Feature - Differentiation: Supporting the Range of Learners
Engaging and supporting learners in making sense of and understanding mathematics are two main goals of the Investigations curriculum. This includes students who are struggling or excelling with certain areas or aspects of mathematics. As part of this, a feature called Differentiation: Supporting the Range of Learners is found in most sessions. This feature includes activity-specific suggestions for Intervention and Extension and for supporting English Language Learners. These suggestions are categorized by instructional strategies that can be generalized and used in other activities and instructional situations.
Here are three Differentiation suggestions from the 4th grade sessions where students are asked to represent fractions on 4 x 6 rectangles.
Lens on Equity
The definition of equity we shared in the Orientation session stated that students must have “the opportunity and support to learn rich mathematics that fosters meaning making [and] empowers decision making” and that “equity demands that responsive accommodations be made as needed to promote equitable access, attainment, and advancement in mathematics education for each student.” What do you think is important to consider in order to ensure students are both engaging fully in rich mathematics and having accommodations made for their individual needs?
Fractions on a Number Line
Modeling fractions on a number line provides students with opportunities to think about fractions as numbers and explore the meaning of fractions with numerators greater than 1. The number line is also an important tool for supporting students in developing their understanding of fractional equivalencies.
In Investigations, students learn to name fractions on a number line using the context of an ant walking along city blocks.
Fractions on a Number Line
Watch the Math Words and Ideas, Fractions on a Number Line presentation to see how students work with fractions on a number line.
How does the number line as used in the presentation support students in visualizing equivalent fractions?
What different understandings of fractions might students gain from representing fractions on a number line versus representing fractions with an area model?
Activity 2: Comparing and Ordering Fractions

In this activity, you will compare fractions to the landmarks 0, 1/2 and 1; compare fractions using a number line; and learn about and use generalized strategies for comparing fractions using reasoning.
As students develop an understanding of fractions and visual images of fractions, they use representations, their knowledge of fraction equivalencies and fraction relationships to compare fractions.
Fractions in Containers
An important strategy for comparing fractions is understanding and using the relationship of fractions to landmark numbers such as 0, 1/2 and 1 whole.
The picture of containers filled with water to different heights provides a visual representation of the landmarks 0, 1/2, and 1.
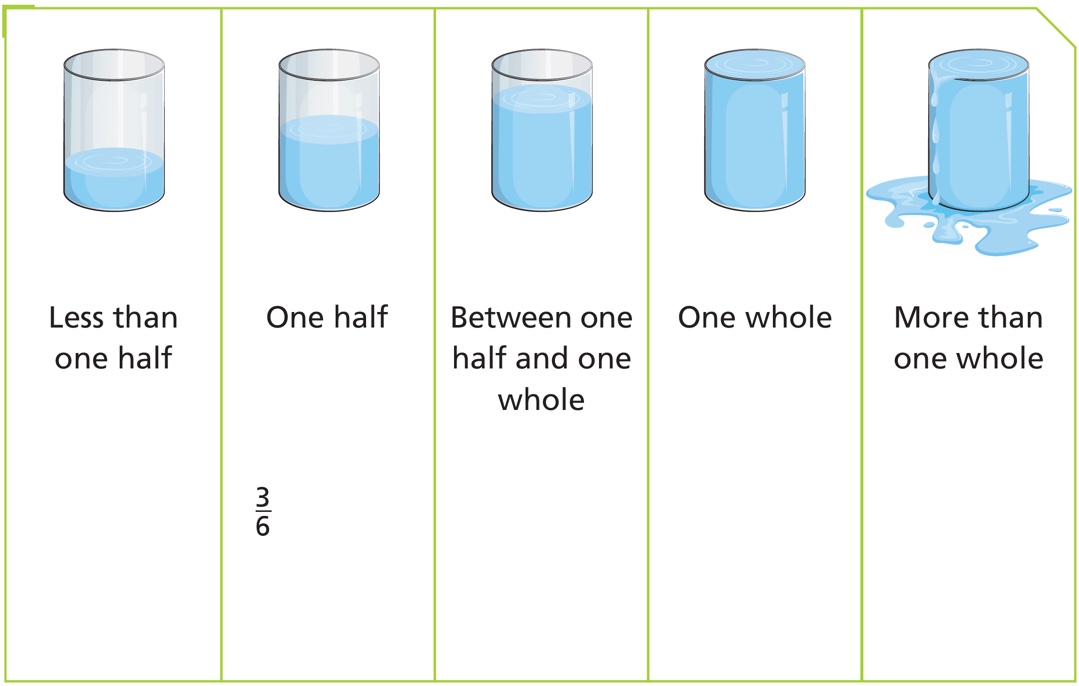
3/6 has already been placed in the column under the one-half full container.
What is another fraction that could be put into the one-half column?
How do you know it belongs there?
Print Fractions in Containers and follow the directions.
What do you notice about all the fractions under the ‘less than one-half’ container? What did you think about as you placed those fractions?
What do you notice about the fractions under the 'between one half and one whole' container? What did you think about as you placed those fractions?
Comparing Pairs of Fractions
Students at first compare fractions using representations such as number lines, rectangles, and pattern blocks. As they become more familiar with fractions and their relationships, they begin to use reasoning to compare fractions.
Which fraction is greater, 3/7 or 1/2?
How did you decide which fraction was greater?
Click [show] to see strategies other teachers may have used.
Third graders use representations such as area models and number lines to compare fractions.
Solve the two problems on Comparing Fractions on a Number Line.
How did you use the number line to determine which fraction was greater?
Read the third grade Math Practices in this Unit essay about how students engage in Mathematical Practice 5: Use appropriate tools strategically as they use tools to compare fractions.
How do the representations students use help them move towards using reasoning to compare fractions?
After students compare a number of fractions with representations or without, they begin to develop more general strategies for comparing fractions.
Read Strategies for Comparing Fractions to learn about strategies for comparing fractions.
Print Fraction Pairs to Compare.
Compare each fraction pair.
Use the strategies you read about in Strategies for Comparing Fractions to determine which fraction is greater.
In the Comparing Fractions Forum share how you determined which fraction is greater 5/2 or 6/3, 2/5 or 1/3 without finding a common denominator and compare your strategies to other participants’ strategies.
Activity 3: Operations with Fractions
In this activity, you will estimate answers to addition and subtraction problems that involve fractions; use representations to solve problems that involve multiplying a whole number and a fraction; and consider similarities and differences between multiplying with whole numbers and multiplying with fractions.
Fourth and fifth grade students build on their understanding of the operations with whole numbers and their understanding of fractions to compute with fractions. They develop an understanding of computing with fractions as they solve problems in context and use representations as they solve the problems.
The computation with fractions students do in fourth and fifth grade includes:
- adding and subtracting fractions and mixed numbers
- multiplying fractions by fractions, mixed numbers and whole numbers
- dividing whole numbers by unit fractions and unit fractions by whole numbers
Addition and Subtraction with Fractions
Students add and subtract with fractions and mixed numbers using a variety of representations such as: 4 x 6 rectangles, rotation on a clock and a number line. These experiences help them visualize and reason about fractional relationships as they put together and take apart fractions.
They move on to adding and subtracting without representations, often by replacing fractions with equivalent fractions with common denominators and then adding or subtracting the fractions.
Closest Estimate: Addition and Subtraction with Fractions
Key to adding and subtracting with fractions is determining what are reasonable answers based on what you know about the size of the fractions and the operations of addition and subtraction.
Look at each problem and the three possible estimates. Decide which of the possible estimates you think is closest to the actual answer without finding common denominators.
Problem A
Problem B
Problem C
What knowledge about fractions and about addition and subtraction did you use to find the closest estimates?
Multiplying Fractions and Whole Numbers
In Investigations, the emphasis of the work is on students using contexts and representations to make sense of multiplying and dividing with fractions and to solve problems involving multiplication or division of fractions. In this activity, you are going to work on multiplying fractions and whole numbers.
A Running Problem
Solve the following problem using a representation and write a multiplication equation that represents the problem.
There is a 2/3 mile loop around a pond near Renaldo’s house.
On Monday, he ran around the loop 4 times.
How many miles did he run?
When you have found your solution and written your equation look at the following possible solutions:
| Solution A | Solution B |
 |
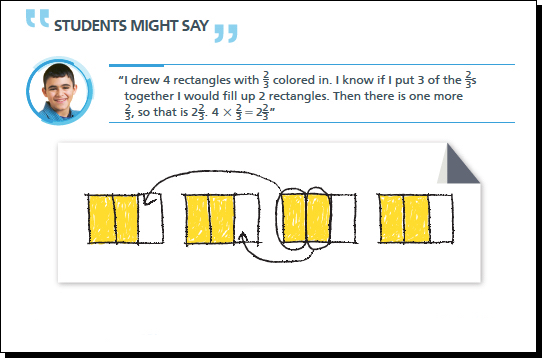 |
You used a multiplication equation to represent this problem. Where do you see the multiplication in this problem? After you have thought about this yourself, look at possible student responses below.

The Big Bicycle Race
Read the following fifth grade problem from Investigations:
Nora, Stuart and Margaret are long-distance bicycle racers. They enter long races that last several days. This year they are entering the Big Bicycle Race. The total distance they have to bike is 480 miles. Each day they are allowed to race for 6 hours.
At the end of Day 1:
- Nora has completed 1/6 of the race.
- Stuart has completed 1/10 of the race.
- Margaret has completed 1/8 of the race.
Who is in first place and who is in last place at the end of day 1?
Without figuring out how many miles they each rode, how do you know?
Fraction Bars
Students in fifth grade use fraction bars to represent and solve problems that involve multiplication with fractions.
Imagine that the length of this fraction bar represents the whole race in this problem – 480 miles.

- Print Big Bicycle Race.
- Read the problem and use the fraction bars to determine the number of miles each participant cycled by the end of Day 1.
- Write an equation that represents how many miles Nora has gone after riding 1/6 of the 480 miles.
Read Why Can We Write 1/6 of 480 as 1/6 x 480? in which a class discusses equations to represent the problem about Nora.
Consider:
How do your equation and representation compare to those of the students in the Grade 5 class?
Where do you see multiplication in this problem?
What is the same about multiplying with fractions and multiplying with whole numbers? What is different?
Read the Math Practices in this Unit essay from fifth grade about how students engage in Math Practice 1: Make sense of problems and persevere in solving them as they work to understand multiplication that involves fractions.
How are students engaged in making sense of problems and perseverance as they work on multiplication with fractions?
Exit Survey
Please take a few minutes to complete the Exit Survey for this course. Your input about your experience in this course is extremely valuable. We use your feedback to continue to improve this course and to help us think about the best ways to offer you and other teachers support in a variety of ways.
Discussion
Once you have completed the work in this session, go to the Session 6 Discussion Forum.
- How did working with different models and representations for fractions affect your own understanding of fractions, comparing them, and operating with them?
- How will it impact your teaching?
Readings
- Developing Meaning for Fractions from 3U6 – Fair Shares and Fractions on a Number Line.
- Visualizing Fraction Equivalencies from 3U6 – Fair Shares and Fractions on a Number Line.
- Mathematical Practice 5 Essay from 3U6 – Fair Shares and Fractions on a Number Line.
- Strategies for Comparing Fractions from 5U3 – Rectangles, Clocks, and Tracks.
- Why Can We Write 1/6 of 480 as 1/6 x 480? from 5U7 – Races, Arrays, and Grids.
- Mathematical Practice 1 Essay from 5U7 – Races, Arrays, and Grids.
The readings above are all published in Investigations in Number, Data, and Space®, 3rd ed. Northbrook, IL: Savvas Learning Company, LLC, 2017.
Key Learnings
- Students use a variety of representations and contexts to make sense of, compare and compute with fractions. Students develop meaning for fractions as equal parts of a whole or several wholes when they work with area representations and as distances and numbers as they work with number line representations.
- Students use representations, their knowledge of fraction equivalencies and fraction relationships to compare fractions. Students then begin to develop more general strategies for comparing fractions.
- Students build on their understanding of the operations with whole numbers and their understanding of fractions to compute with fractions.
- The emphasis of the work with multiplication and division with fractions in Investigations is on students using contexts and representations to solve multiplication and division problems that involve fractions and to help them expand their understanding of multiplication and division to include fractions.