Overview

Session Summary

In this session you will examine the complexities of counting – the understandings needed to count a group of objects and the progression from counting by ones to counting by groups. You will consider how students develop an understanding of the structure of the number system including the written number sequence, patterns in the number system, and the place value of numbers.

You will examine counting scenarios and student work on counting and then explore what they show the students already understand about counting and what they do not yet understand. You will learn about the activities that encourage students to count by groups and then count a set of objects in different ways yourself.

Mathematics in this session

• Examine the understandings needed to count a set of objects
• Consider aspects of learning the counting sequence and making sense of the structure of the number system
• Examine how students move from counting by ones to counting by groups

Common Core Alignment

The content in this session is aligned to the following Common Core State Standards and Math Practices:

MATH STANDARDS

Counting and Cardinality K.CC
K.CC.4a, b, c; 5

4. Understand the relationship between numbers and quantities; connect counting to cardinality.
   1. When counting objects, say the number names in the standard order, pairing each object with one and only one number name and each number name with one and only one object.
   2. Understand that the last number name said tells the number of objects counted. The number of objects is the same regardless of their arrangement or the order in which they were counted.
   3. Understand that each successive number name refers to a quantity that is one larger.
5. Count to answer “how many?” questions about as many as 20 things arranged in a line, a rectangular array, or a circle, or as many as 10 things in a scattered configuration; given a number from 1–20, count out that many objects.

Counting and Cardinality
K.CC.3

Know number names and the count sequence.

3. Write numbers from 0 to 20. Represent a number of objects with a written numeral 0-20 (with 0 representing a count of no objects).

Number and Operations in Base Ten

1. NBT.1
   Extend the counting sequence.
   1. Count to 120, starting at any number less than 120. In this range, read and write numerals and represent a number of objects with a written numeral.

      Understand place value.

2. NBT.1b
   1. Understand that the three digits of a three-digit number represent amounts of hundreds, tens, and ones; e.g., 706 equals 7 hundreds, 0 tens, and 6 ones. Understand the following as special cases:
      2. The numbers 100, 200, 300, 400, 500, 600, 700, 800, 900 refer to one, two, three, four, five, six, seven, eight, or nine hundreds (and 0 tens and 0 ones).

MATH PRACTICES

MP1 Make sense of problems and persevere in solving them.

MP7 Look for and make use of structure

You may also wish to review the full set of Common Core State Standards in Math and/or videos of the Math Practices enacted in Investigations.

Part A: Star Counting Activity

Overview

In this activity, you will work on an adult counting activity -- counting the number of stars on a screen. You will consider what you need to understand to be able to accurately count the set of stars.

Counting is the foundation for understanding the number system and for almost all the number work in the primary grades. In Kindergarten students begin by counting small quantities of objects. By the end of second grade most students are counting larger quantities of objects by groups.

For adults, counting is usually a simple task. However there is a lot we need to know and pay attention to in order to count a set of objects.

Star Counting Activity

Try to count the number of stars in the starry night image below. Then answer the following questions:

After you have considered what you needed to know to count the number of stars, click on the Show link to see observations other participants have made in response to this activity.

To consolidate your understanding, review the Teacher Note, Counting is More Than 1, 2, 3.

Click on the Show link for a summary of some of the important ideas in this Teacher Note.

Part B: Counting Scenarios

Overview

In Part B of this activity, you will read three scenarios of students counting and then analyze and discuss what the scenarios show the students understand and don’t yet understand about counting.

Counting Scenarios

Observing students as they count can give you information about what they understand about counting a set of objects and what they have not yet figured out. This is information that can be difficult to obtain from only looking at what a student records on paper.

In the Counting Scenarios discussion forum, three scenarios are listed. Respond to at least one scenario, sharing the following information:

1. What did the student do?
2. What do you think the student understands about counting?
3. What do you think the student does not yet understand about counting?
4. What questions might you want to ask the child?

Please note: Each of the scenarios gives only a little information about the student. If these were students in your classroom you would, of course, have a lot more information about the students based on your prior observations. For this activity, please just use the information in the scenarios to discuss what the student might understand and not understand.

Counting Sequence and the Number System

Overview

In this activity you will analyze errors students might make when writing numbers in sequence. You will explore the game Missing Numbers on a 100 Chart and consider how students might figure out the missing numbers.

Students have many opportunities throughout the curriculum to work on learning both the oral and written number sequence and the structure of the number system. In Kindergarten, students work on the number sequence up to 20. In first and second grade, students look for patterns in the number sequence and work on the structure of the number system up to and above 100. In later grades they continue to examine patterns in the number system and the structure of the number system as they work with very large numbers such as 10,000 or 100,000 and very small numbers such as 0.001.

Counting Strips

In first grade and then in second grade, students do an activity called Counting Strips - they start at zero and write the numbers vertically in sequence, as high as they can, on a strip of adding machine tape.

As students create their counting strips teachers can learn not only how high students can count, but learn some about what students understand and don’t yet understand about the written number sequence.

Watch the VoiceThread below to learn more.

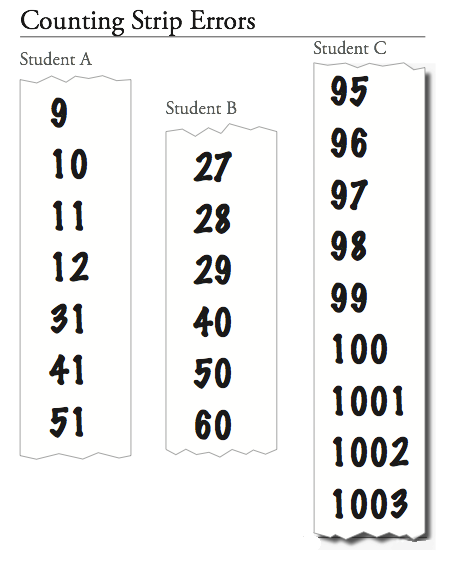
Click on the Show link to see parts of three strips with common errors first grade students make. Look at each one and consider

• the mistake the student made
• what the mistake shows about what the student might already understand about the written number sequence, and
• what you think the student does not yet understand about the written counting sequence.

1,000 Book

In first grade after students have created their own counting strip, the teacher creates a horizontal counting strip of the numbers 1 to 100. The class then cuts the counting strip into rows of 10 and creates a 100 Chart. A 100 Chart is a tool that is used throughout the grades to learn about the number system. Some students also use the 100 Chart to help them solve addition, subtraction, multiplication and division problems. In later grades students use multiple 100 charts to examine the structure of 1,000 and 10,000.

In a fourth grade activity students are given ten blank 100 charts and they create a 1,000 book from the charts, filling in enough numbers on each page so they can locate any number. You will be looking at a few selected pages of a 1,000 book in the following activity. Your task is to

• figure out what numbers belong in specific squares, and
• where specific numbers are located.

Review the three sample pages from a 1,000 Book in the annotation activity and enter your responses to the prompts on each page. Be sure to click Submit Responses when you are done. You can also view others’ responses by clicking Participant Responses at the bottom of the page.

Missing Numbers

In first grade students play a similar game called Missing Numbers in which some of the numbers on the 100 Chart are covered and students try to figure out which numbers are covered. As students create their counting strips and play Missing Numbers they begin to notice patterns in the number system.

Once you have considered this question, click the Show link to see how other teachers have responded.

Counting by Groups

Overview

In this activity you will learn about the work students do counting things that naturally come in groups. You will look at student work for a second grade problem about how many fingers are in the class and consider the strategies students used to solve this problem. You will also explore the progression that students move through from counting by ones to counting by groups.

How Many Eyes

Children begin counting objects that are in groups early on in Kindergarten. In a data activity called How Many Eyes? Kindergartners use such strategies as each child taking two cubes to represent their two eyes, or having each child count the next two numbers in sequence as they count around the class. In first and second grade, students are introduced to many activities in which they count by 2’s, 5’s and 10’s. In particular they count objects that naturally come in groups such as eyes, legs on people and animals, fingers on people. All these activities set the foundation for later work with multiplication.

Take a look at the chart below.

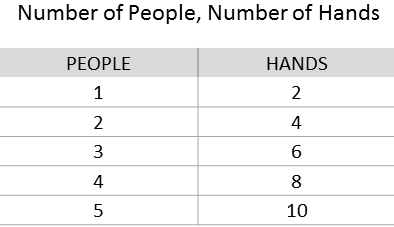
After first grade students solve a problem about how many hands 8 people have, the whole class works together to fill out a chart like this. This chart identifies the numbers of hands on an increasing number of people.

As numbers get larger, students’ strategies may vary considerably. What is important is that students have ways of solving problems that make sense to them and that they begin to explore number patterns and to count by groups of objects in a meaningful way.

How Many Fingers?

Prior to this activity, students are asked to find out how many legs there are in their classroom. In this activity they are asked how many fingers are in the room and to explain how they figured it out.

When looking at student work, especially for the first time, it’s easy to get distracted by things we see on the paper that don’t necessarily relate to the child’s thinking about the problem, such as their ability to write large numbers accurately. Please try to focus instead on the student’s thinking. You may wish to review the DIET protocol for looking at student work.

Counting Objects in Groups

When students count the eyes in the class in Kindergarten, most students will count them by ones. When figuring out how many fingers are in the class, most second graders will count by groups. Students generally progress from counting by ones to counting by groups. When you observe students in your class counting objects that are in groups you will probably notice a range of how they count.

Review the page Counting Objects in Groups. The examples here are from a first grade activity in which the students are given an envelope containing a set of squares. The envelope contains a mixture of squares grouped in different ways – some are single squares, some are grouped in twos and some are grouped in fives. The students figure out the total number of squares in the envelope and record how they figured out the number of squares.

The work students do on counting and then counting by groups is the foundation for the work they do with place value and understanding the number system. Most students in second grade make a critical shift from thinking and working primarily in 1s to thinking and working with groups of 10s and 1s. Understanding the 10:1 relationship that one 10 is equal to ten 1s is essential for understanding the base ten number system. However there is more that students need to know in order to understand the place value of numbers.

Understanding Place Value

• Understanding that 10 ones equals 1 ten
  
• Understanding what each numberal in a number respresents
  The 3 in 32 stands for 3 tens, and the 2 stands for 2 ones.
• Understanding that a number can be expressed as 10s and 1s in different ways.
  32 is 3 tens and 2 ones, but it is also 2 tens and 12 ones.
• Understanding a number's relationship to other numbers
  217 is closer to 200 than to 300. It is 100 more than 117

Discussion

What have you uncovered about the complexities and importance of counting? Use specific examples from this session.

Go to the Forum

Key Learning

• Counting is the foundation for understanding the number system and almost all the number work in the primary grades. While counting may seem simple it is actually quite complex and involves the interplay between a number of skills and concepts.
• Observing students as they count can give you information about what they understand about counting a set of objects and what they have not yet figured out.
• Students have many opportunities throughout the Investigations curriculum to work on learning both the oral and written number sequence and to making sense of the structure of the number system.
• The work students do on counting by groups is the foundation for the work they do with place value and the work they do later with multiplication.
• In order to understand the place value of numbers students need to understand: what each number represents, that one 10 is equal to ten 1s, that a number can be expressed as tens and ones in different ways and understand a number’s relationship to other numbers.

This session is aligned with the following K-2 Units in Investigations.