Overview
Session Summary
This session focuses on division problems involving fractions and the importance of using contexts and representations to extend understandings about the operation of division to include fractions. The session also focuses on reviewing the teaching and learning of fractions across Grades 2-5.
Fractions and Division
As students begin to divide with fractions, they extend their understanding of the operation of division. They need to examine their understandings of the operation of division and decide if the strategies and reasoning they use to solve division problems with whole numbers will still work, and make sense, when solving division problems involving fractions.
Watch Investigations author Keith Cochran discuss how students engage in thinking about division problems that involve dividing a non-zero whole number by a unit fraction or a unit fraction by a non-zero whole number.
Read the Teacher Notes, Strategies for Multiplying and Dividing With Fractions (this is only the section on division strategies) and Dividing with Fractions to learn more about understanding division problems involving fractions.
Think about both the video and the Teacher Notes.
What role do story contexts and representations play in helping students solve problems involving division with fractions?
What are the two interpretations of division that 5th graders usually draw upon as they begin work with division problems that involve fractions?
Materials
Below is a list of materials you will need for each activity in this session. You will also find these materials listed at point of use in the session.
Pencil and paper (or computer) are needed for each activity.
Activity 1 Activity 2Activity 3
- None
Activity 1: Dividing With Whole Numbers and Unit Fractions
In this activity you will solve division problems involving fractions by using representations and reasoning and examine the ways in which students’ understanding of the operation of division expands when students solve division problems with fractions.
Groups of Groups: Extending Ideas About Division
As students in Grades 3 and 4 begin their work with division and solve word problems, they are asked to identify what they know and don’t know in a variety of problems. They come to recognize that in some problems (multiplication situations) they know the number of groups, and the number in each group, but not the number in all the groups and in other problems (division situations) they know the number in all the groups and either the number of groups, or the number in each group. In whole group discussions, students fill in tables like the one below, showing what’s known and not known, and what equations represent the problem.
Number of Groups |
Number in Each Group |
Number in all the groups |
Equations |
|
|
|
|
|
|
|
|
|
|
|
|
Terrence has 12 cups of flour. If he needs 2 cups of flour to make a pan of brownies, how many pans of brownies can Terrence make?
Write two equations that represent the problem - a multiplication equation (with a missing factor) and a division equation.
For this problem, the table would look like this:
Number of Groups |
Number in Each Group |
Number in all the groups |
Equations |
? |
2 |
12 |
12 ÷ 2 = ? ? x 2 = 12 |
Terrence has 3 cups of flour. If he needs 14 cup of sugar to make one jumbo pancake, how many pancakes can Terrence make?
Terrence has 14 of a jumbo pancake. If he shares it equally with two friends, how much of the jumbo pancake will each person get?
Click [show] to see a completed table for these two problems. Does this match the table you created? If not, what is different?
Number of Groups |
Number in Each Group |
Number in all the groups |
Equations |
? |
14 |
3 |
3 ÷ 14 = ? ? x 14 = 3 |
3 |
? |
14 |
14 ÷ 3 = ? 3 x ? = 14 |
Terrence has 3 cups of flour. If he needs 14 cup of sugar to make one jumbo pancake, how many pancakes can Terrence make?
Terrence has 14 of a jumbo pancake. If he shares it equally with two friends, how much of the jumbo pancake will each person get?
Where do you see each part of the word problem in your representation? Each part of the equation? Where do you see the operation of division?
Math Words and Ideas: Dividing Whole Numbers and Unit Fractions
Watch the two Math Words and Ideas shown below (Dividing a Fraction by a Whole Number and Dividing a Whole Number by a Fraction) and do at least 1 or 2 problems in the “Try It” section. (To get to “Try It” screen click the arrow in lower right of screen to advance to the next slide.)
Dividing a Fraction by a Whole Number
Dividing a Whole Number by a Unit Fraction
Think about the operation of division and the two Math Words and Ideas presentations. What seems the same or different about division with whole numbers and division involving fractions?
Dividing with Whole Numbers and Unit Fractions
In the Teacher Note you read in the Orientation Session it was suggested that students should have two interpretations of division through their work with whole numbers (either determining how many groups- how many 3s in 6? - or how many in each group- if I divide 6 into 3 parts, how much in each part?). The Teacher Note suggests using these interpretations of division when working on division with fractions will be helpful to students. For example when solving 3 ÷ 14, students can think, “how many 14 s are in 3”, and when solving 14 ÷ 3, students can think, “if I divide 14 into 3 parts, how big will each part be?" You might want to keep these ideas in mind, as well as the MWI presentations you viewed as you solve problems that involve division with fractions in this session.
Use a representation to solve each of the following problems:1. Avery has 6 yards of ribbon. He needs 13 yard to make one bow. How many bows can Avery make?
2. Six students equally shared 12 of a brownie. What fraction of the whole pan of brownies did each student eat?
What division equation represents each problem?
What multiplication equation represents each problem?
Use these steps from the LASW protocol to examine each piece of student work. Cite evidence from the student work to support your responses.
Describe what the student did to solve the problem.
- What does the student seem to already know or understand?
- What mathematics does the student seem confused about, or still seem to be working on?
- What might be some mathematical next steps for the student?
Students A, B and C are solving the problem: Avery has 6 yards of ribbon. He needs 13 yard to make one bow. How many bows can Avery make?
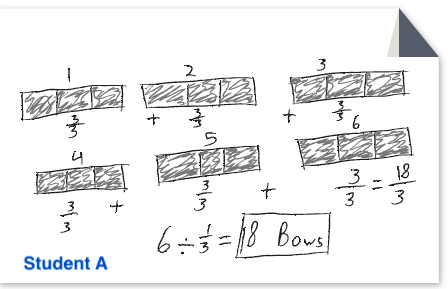 |
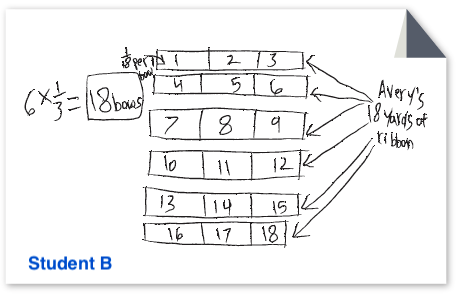 |
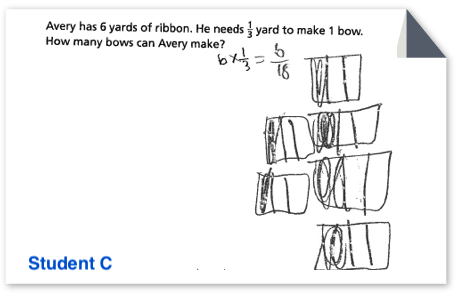 |
Students D, and E are solving the problem: Six students equally shared 12 of a brownie. What fraction of the whole pan of brownies did each student eat?
 |
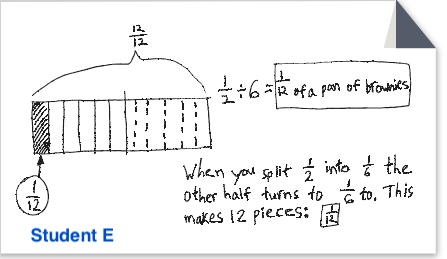 |
Activity 2: Division with Fractions
In this activity, you will use representations and reasoning to solve division problems with fractions and mixed numbers.
Division with Fractions
In Investigations division problems that involve fractions only include dividing a whole number by a unit fraction or a unit fraction by a whole number. However, it is important to consider where students’ work with division of fractions extends beyond Grade 5. Many of us have only solved division problems involving fractions as we were taught, using a rule: “invert the divisor (the second fraction) and multiply.” In this activity you are going to solve division problems that include mixed numbers and non-unit fractions to extend your own understanding of this work.
Read the problem below. Is the answer going to be more or less than 1? How do you know? You may want to think about whether the questions that go with either of the two interpretations of division discussed in Activity 1 would be helpful here.
As work with division of fractions continues, keeping track of the whole-part relationship becomes increasingly important. Look at your representation:
What does the 112 represent? the 12 ?
Where do you see the answer?
Where do you see the division? Do you see any multiplication? Where?
Is the answer going to be greater than or less than the answer to the problem with bows that required 12 a yard? How do you know?
Is the answer going to be a whole number? How do you know?
Consider these two solutions to this problem:
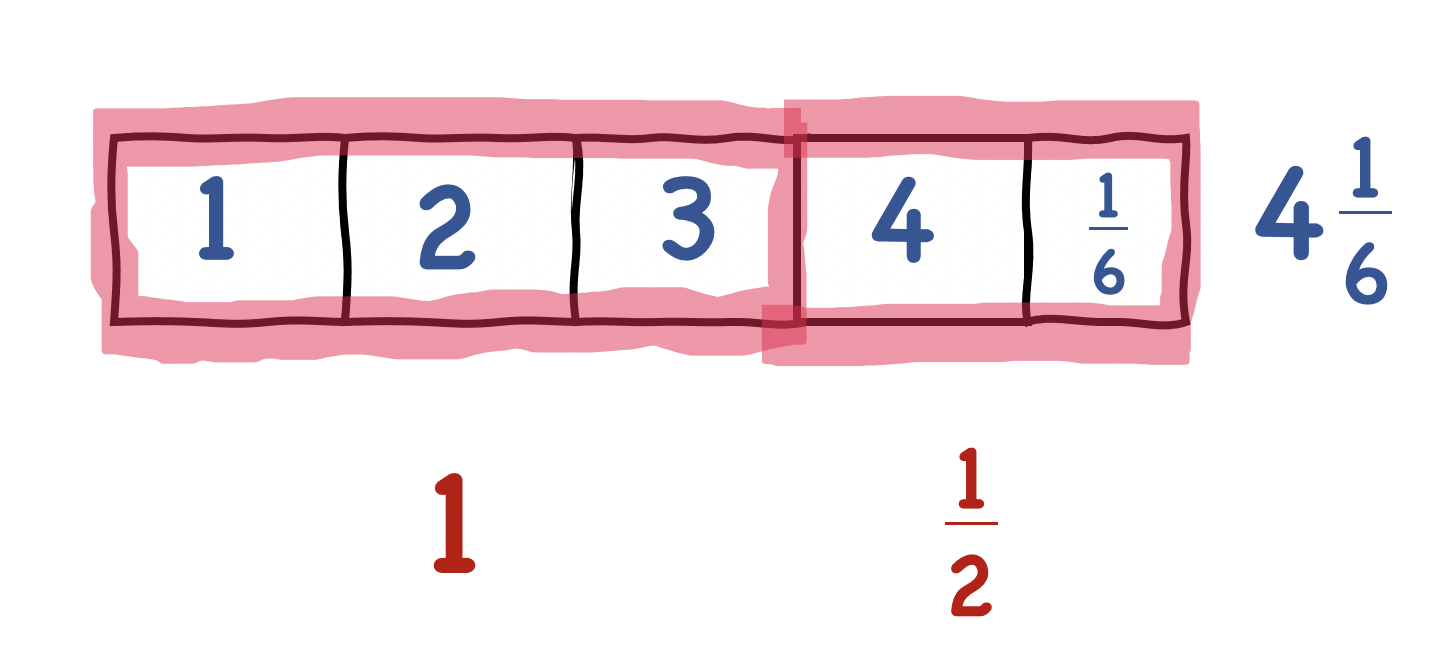
Alex solved this problem by using a fraction bar with a length of 112 (yards). First, he divided the 1 into thirds and wrote “1” “2” "3” to show 3 bows can be made with 1 yard of ribbon. He marked one more "13 ” in the 12 yard of ribbon remaining and wrote a “4” to show a 4th bow. Alex knows that 13 + 16 = 12 so there is 16 left, and labels his answer as "4 16" (bows).
Shandra solved the problem by using pattern blocks, using the hexagon as the whole. In her solution, the hexagon represents 1 yard of ribbon, and the trapezoid represents 12 yard. Shandra divided the hexagon into thirds (using rhombuses) to show each bow. There was one “piece” of ribbon left (which is equivalent to a triangle or 16 of a hexagon/yard) after the 4th bow, and Shandra got the answer of 4 12 bows.
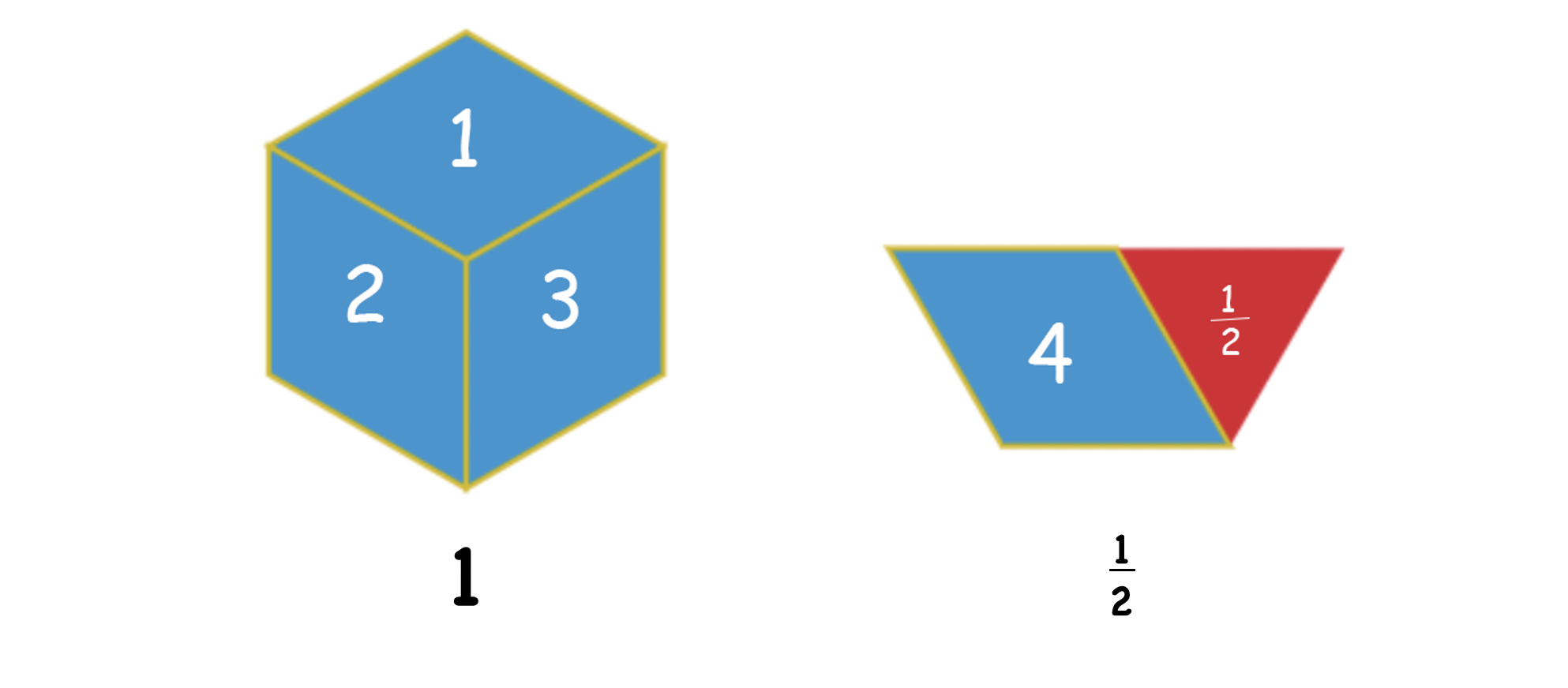
Examine both representations.
What does the 1 12 represent?
What does the 13 represent? Where do you see 13 s in each representation?
Which student is correct? How does 4 16 make sense as an answer? How does 4 12 ?
Making Sense of the Answer
To determine which answer, 4 16 or 412 is correct, it’s important to understand what unit the answer refers to. There is 16 of a yard of ribbon left, and since the question is how many bows can Cheyenne make, you have to figure out how much of a bow is 16 yard of ribbon, or what fraction of 13 (the amount of ribbon needed to make a bow) is 16 ?
Look one more time at Shandra’s representation to think about this idea visually. The hexagon equals one yard of ribbon, the trapezoid equals 12 yard of ribbon, and the rhombus represents 1 bow (made of 13 yard of ribbon). You can see that a triangle is left in the trapezoid. That leftover triangle represents 16 yard of ribbon (because the triangle is 16 of the hexagon). However, the problem asks how many bows Cheyenne can make. Since one rhombus equals one bow and it takes two triangles to make one rhombus, one triangle is equivalent to 12 of a rhombus or 12 of a bow meaning Cheyenne can make 412 bows.
By using contexts, representations, and reasoning, it is possible to make sense of, and understand dividing with fractions, and not to depend on a rule that has been taught to solve division problems involving fractions.
Using Pattern Blocks to solve Division Problems involving Fractions
Pattern blocks are a useful tool when working with fractions, because if the hexagon is the whole, the set of fractions is limited to halves, thirds, and sixths so it is somewhat easier to see the relationships between these fractions. Using pattern blocks to solve division problems involving fractions provides an opportunity to better understand conceptually, concretely, and visually what each part of the problem represents.
Use pattern blocks to complete the following activities. If you do not have physical pattern blocks, use these digital pattern blocks.
Use pattern blocks to solve this problem from above. (You may want to look at Shandra’s solution to 2 12 ÷ 13 to help you get started.)
Compare the representation you used to solve this problem originally to your representation using pattern blocks. How are they the same? Different? Did using the pattern blocks reveal any new understanding of dividing by fractions?
You may find the following problems challenging, particularly if you are using the digital pattern blocks. As you try to solve the problems, be thinking about what is challenging, what you’re learning about division with fractions, as well as what you might do if you get stuck. (A reminder-trying a similar problem with whole numbers is often a useful strategy, and it’s likely you’ve discovered other useful strategies as you’ve worked in this session.)Before solving each of these problems, consider these questions: Is the quotient going to be more or less than 1? Will the quotient be a whole number? How do you know?
Use pattern blocks to represent and solve the problems. Consider the hexagon as the whole.
1. 2 ÷ 13
2. 1 23 ÷ 13
3. 12 ÷ 23
4. 23 ÷ 12
Consider your experience solving these problems. What was challenging? What ideas helped you solve the problems? What did you do when you got stuck? How do you know your answer is reasonable?
Activity 3: Solving Problems with Fractions
In this activity you will answer True/False statements and Closest Estimate problems using reasoning and your understanding of fractions and the meaning of the operations. You will also reflect on the teaching and learning of fractions in Grades 2-5.
True False Statements
In this activity, you’re going to continue thinking about dividing fractions by fractions.
Using only reasoning, determine if the following problems are True or False. Explain how you know. (It may help you think of these as missing factor problems "what times 15 is 18?" or as “how many 15s will go into 18?")
1. 18 ÷ 15 < 25 ÷ 15
2. 14 ÷ 10 < 13 ÷ 10
3. 2 12 ÷ 34 > 5 ÷ 34
4. 12 ÷ 13 < 12 ÷ 15
5. 23 ÷ 14 < 23 ÷ 13
Which of these problems do you find easy? Why? Which did you find challenging? Why? What knowledge about fractions and division did you use to solve the problems?
Closest Estimate Problems
Closest Estimate is a Ten-Minute Math activity in Grades 3-5. You solved similar problems in Session 4. In this activity, students view a problem along with three possible estimates. They determine which of the three choices is closest to the actual answer (without solving the problem itself) and are expected to explain their reasoning. They are also asked to think about whether the closest estimate is greater than or less than the actual answer. Closest Estimate supports work with computational fluency as they practice making estimates (is the answer reasonable?). Students make estimates based on what they know about the operations and the magnitude of the numbers. By determining whether the closest estimate is greater than or less than the actual answer, students also deepen their understanding of each operation. You’re going to solve some Closest Estimate problems involving all 4 operations.
Using reasoning about the magnitude of the numbers, and your understanding of the operations, determine which estimate is closest for each of these problems without doing the actual computation, and explain how you know. Also determine whether the actual answer to the problem will be less than or greater than the actual answer.| 1. 2 47 + 5 12 ≈
|
7 12 | 8 | 8 12 | |||
| 2. 12 1213 - 4 12 ≈ | 8 12 | 9 | 9 12 | |||
| 3. 27 x 126 ≈ | 20 | 30 | 40 | |||
| 4. 2 38 x 8 ≈ | 6 | 12 | 20 | |||
| 5. 1 12 ÷ 18≈ |
10 | 12 | 14 | |||
| 6. 34 ÷ 14 ≈ | 1 | 2 | 3 |
Which of these problems were easy for you to solve, including whether the estimate was greater or less than the actual answer? Which were challenging? Why?
How did you use your understanding of the operations and of fractions as you solved these problems, and considered the actual answer?
Did you use anything you learned in the sessions of this course to solve these problems?
Reflecting on the Learning and Teaching of Fractions
We have all had different experiences learning, teaching and working with fractions. Some of us may have found that learning about fractions was the first time we felt we didn't understand math; we may feel comfortable using fractions because of experiences at home with cooking, carpentry or sewing; we may have felt that it was through teaching fractions that we began to understand them.
Think about some of your own experiences learning about, working with or teaching fractions. Post your response to one of these two questions in the Fraction Experiences Forum.
1.) Share a memory you have of learning about fractions in school, working with fractions in your home or community, or teaching fractions. What effect did this experience have on your understanding of fractions? On your feelings about fractions?
2.) How has taking this course helped deepen your understanding of fractions and the operations? How will it impact your teaching of fractions and your understanding of how students make sense of fractions?
Once you've posted your response respond to at least 2 of your colleagues' posts.
Lens on Equity
In Chapter 3 of their book, Impact of Identity in K-8 Mathematics, the authors focus on the experiences and contexts that can contribute to the development of a “K-8 mathematics teacher identity–an identity that consists of knowledge and lived experiences, interweaving to inform teaching views, dispositions, and practices to help children learn mathematics.” (p. 27) They also write: “The nature of the mathematics learning experience that a teacher had in his or her own schooling has a powerful influence on the mathematics teacher identity that he or she develops.” (p. 28)
Think about your own identity as a learner of mathematics, about your “mathematics teacher identity”. How has your view of yourself as a learner and teacher of mathematics, changed? What event or events seemed to cause the greatest shift in your thinking about yourself as a “doer” and “teacher” of math? How do you think this course might impact your teaching of mathematics going forward?
Exit Survey
Please take a few minutes to complete the Exit Survey for this course. Your input about your experience in this course is extremely valuable. We use your feedback to continue to improve this course and to help us think about the best ways to offer you and other teachers support in a variety of ways.
Forums
Once you have completed the work in this session, go to the Session 6 Discussion Forum. Respond to one of the discussion threads in the forum, or start your own thread about a question, idea, or topic of interest that is related to the content of the session.
After you have posted your comments, take time to read others’ posts and respond to at least 2 of your colleagues.
Return to the Fraction Experiences Forum and respond to at least 2 of your colleagues' posts.
Key Learnings
- Previous understandings of the operation of division are expanded when solving division problems with fractions
- Representations and story problem contexts help students make sense of dividing whole numbers and unit fractions
- Students use their understanding of fractional quantities and their relationships, and the operation of division to solve division problems involving whole numbers and unit fractions
Readings
Teacher Note 2: Strategies for Multiplying and Dividing with Fractions(p. 233) from Grade 5 U7 Races, Arrays, and Grids.
Teacher Note 4: Dividing with Fractions from Grade 5 U7 Races, Arrays, and Grids.
The readings above are all published in Investigations in Number, Data, and Space®, 3rd ed. Northbrook, IL: Savvas Learning Company, LLC, 2017.