Overview

Session Summary

The overall purpose of this session is for you to engage in and reflect on the mathematics of combining and comparing fractions and to become familiar with some approaches to fractions found in Investigations. This approach is different from the computational procedures most of us were taught in school. The activities support the development of strategies that build on familiar relationships among fractions.

In this session you will use a variety of representations to develop mental images of fraction relationships. You will connect fraction names to parts of a group, explore ways to make wholes from fractional parts, generate addition equations to describe combinations of fractions, and develop a repertoire of ways to compare fractions, recognizing that common denominators is only one of many ways to do this.

EQUITY MOMENT

This session typically brings out a great deal of emotion. As one workshop leader described, “Many people have tears of panic coming into the session and tears of triumph after the session.” This is a session where people are easily silenced by the content of the math and where gender differences surface when working on group activities and presenting work.

During many of the activities males in particular may begin to dominate the discussions. In many instances, it is not the men themselves that are pushing for this kind of involvement but rather that women begin to “take a back seat” and encourage men to answer questions related to this work.

You are encouraged to reflect on the following questions and statements:

  • Consider your experiences as a child with fractions. How does this relate to your experience with fractions as an adult?
  • It is important not to single out any particular group during group work or discussions around mathematics. This includes males, but also girls, children of color, students learning English as a Second language, etc.
  • Why is it that men - particularly men who teach higher grades - seem to feel more comfortable working with fractions?"
  • What do we want students to be able to do when working on fractions? How would we set up the classroom so that all students have an opportunity to participate in some way?
  • Think about ways students in your class participate. When are they silenced? How do you as a teacher intervene?

Mathematics in this session

  • Identify fractional parts of an area
  • Identify fractional parts of a group
  • Find combinations of fractions that are equal to 1 and to other fractions
  • Use representations and landmarks to compare, order, and combine fractions

Common Core Alignment

The content in this session is aligned to the following Common Core State Standards and Math Practices:

MATH STANDARDS

Number And Operations—Fractions 3.NF

Develop understanding of fractions as numbers.

  1. Understand a fraction 1/b as the quantity formed by 1 part when a whole is partitioned into b equal parts; understand a fraction a/b as the quantity formed by a parts of size 1/b.
  2. Understand a fraction as a number on the number line; represent fractions on a number line diagram.
    1. Represent a fraction 1/b on a number line diagram by defining the interval from 0 to 1 as the whole and partitioning it into b equal parts. Recognize that each part has size 1/b and that the endpoint of the part based at 0 locates the number 1/b on the number line.
    2. Represent a fraction a/b on a number line diagram by marking off a lengths 1/b from 0. Recognize that the resulting interval has size a/b and that its endpoint locates the number a/b on the number line.
  3. Explain equivalence of fractions in special cases, and compare fractions by reasoning about their size.
    1. Understand two fractions as equivalent (equal) if they are the same size, or the same point on a number line.
    2. Recognize and generate simple equivalent fractions, e.g., 1/2 = 2/4, 4/6 = 2/3). Explain why the fractions are equivalent, e.g., by using a visual fraction model.
    3. Express whole numbers as fractions, and recognize fractions that are equivalent to whole numbers. Examples: Express 3 in the form 3 = 3/1; recognize that 6/1 = 6; locate 4/4 and 1 at the same point of a number line diagram.
    4. Compare two fractions with the same numerator or the same denominator by reasoning about their size. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with the symbols >, =, or <, and justify the conclusions, e.g., by using a visual fraction model.

Extend understanding of fraction equivalence and ordering. 4.NF

  1. Explain why a fraction a/b is equivalent to a fraction (n x a)/(n x b) by using visual fraction models, with attention to how the number and size of the parts differ even though the two fractions themselves are the same size. Use this principle to recognize and generate equivalent fractions.
  2. Compare two fractions with different numerators and different denominators, e.g., by creating common denominators or numerators, or by comparing to a benchmark fraction such as 1/2. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with symbols >, =, or <, and justify the conclusions, e.g., by using a visual fraction model.

Build fractions from unit fractions by applying and extending previous understandings of operations on whole numbers.

  1. Understand a fraction a/b with a > 1 as a sum of fractions 1/b.
    1. Understand addition and subtraction of fractions as joining and separating parts referring to the same whole.
    2. Decompose a fraction into a sum of fractions with the same denominator in more than one way, recording each decomposition by an equation. Justify decompositions, e.g., by using a visual fraction model.
      Examples:
      3/8 = 1/8 + 1/8 + 1/8
      3/8 = 1/8 + 2/8
      2 1/8 = 1 + 1 + 1/8 = 8/8 + 8/8 + 1/8

Number And Operations—Fractions 5.NF

  1. Interpret a fraction as division of the numerator by the denominator (a/b = a ÷ b).

MATH PRACTICES

MP1 Make sense of problems and persevere in solving them.

MP3 Construct viable arguments and critique the reasoning of others.

MP5 Use appropriate tools strategically.

MP6 Attend to precision.

You may also wish to review the full set of Common Core State Standards in Math and/or videos of the Math Practices enacted in Investigations.

Visual Representations of Fractions

Overview

The fraction work in Investigations focuses on visualizing and reasoning about fractions. Students need to understand the meaning of fractions and develop mental images for fraction relationships before they learn computational procedures.

In this session you will participate in many of the fraction activities that Investigations students do in grades two to five. You will build on your own “fraction sense” by figuring things out and learning from others.

We’ll start by thinking about how fractions can be represented.

EQUITY MOMENT

Take a moment to reflect on your feelings when working with fractions as a student (or as a teacher). This will provide a context for our discussion around fractions, access to mathematical thinking and opportunities for student learning.

Visual Representations of Fractions

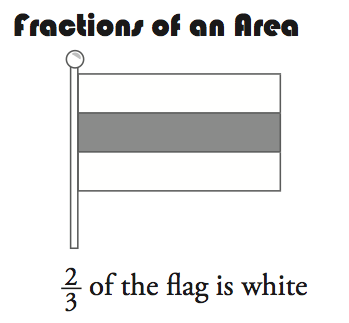
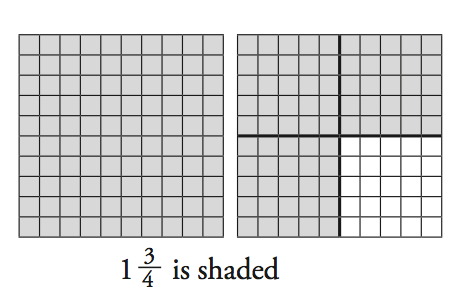
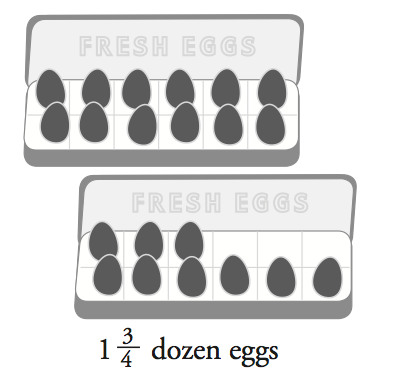
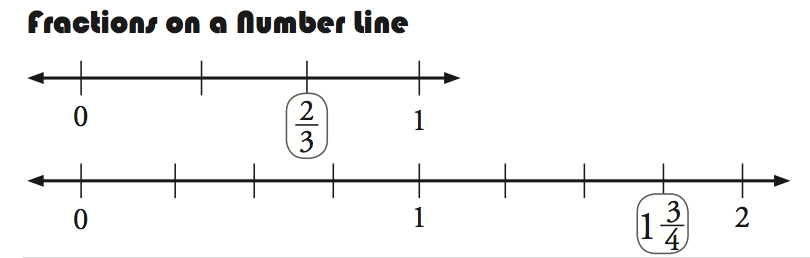
On paper, write 2/3 and 1 3/4 and sketch illustrations for these fractions.

Next, review the three fraction representations below. Which drawing is most similar to what you sketched? Or, did you use a representation distinctly different from these three?

  • Sample 1
  • Sample 2
  • Sample 3

NOTES:

  • Through the area and set representations, students develop an understanding that a fraction shows the relationship between two numbers, e.g., comparing the part (2 white stripes on the flag) to the whole (3 equal sized stripes on the flag).
  • The number line representation emphasizes that a fraction is a quantity.
  • Some of you are likely to have shaded circular areas as "pizzas" or "pies." This is an example of fractions of an area.

In this session we will make use of all these representations as we work on activities about understanding fraction relationships.

Fractions of a Group: Guess My Rule

Now you will explore fractions of a set by making statements about characteristics of a group of people. You will also see examples of the ‘fractions of a set’ problems that students work on in grades two to five.

Our "set" will be based on the group of people below. We will describe characteristics that fit some of these people and use fractions to name equal parts of the group.

5 different people

How would we describe the portion of the group that are:

  • Wearing green?

    1/5

  • Have brown shoes?

    2/5

  • Wearing a watch?

    3/5

What portion of the group does not fit the characteristics?

Next review the illustration below.

8 different people

How would we describe the portion of the group that are:

  • Wearing green?

    1/8

  • Have blond hair?

    2/8 or 1/4

  • Wearing glasses?

    2/8 or 1/4

Now that the number in the whole group has changed, how have the statements changed?

By playing Guess My Rule and identifying fractions of a group, we see that a fraction represents a relationship between two numbers, part of the group that shares a characteristic and the number of people in the whole group.

Student Work

Now read through some examples of other 'Fractions of a Set' problems that students solve in grades two to four.

Features of these problems include:

  • In grade 1, students find halves and fourths of circles and squares.
  • In grade 2, students find half of many different sized sets. They also work with thirds and fourths of sets.
  • In grade 4, students are asked to name a fractional amount and the quantity of the set that fraction names.

EQUITY MOMENT

When working with students to identify characteristics of a group in the Guess My Rule activity, always look for positive attributes. Why might this be important? Are there any attributes that may be considered troubling to students? How do you (or how can you) avoid them? How do you set up a community in your class that makes it a safe environment to do activities such as this?

Fractions of an Area

Overview

In this activity, we will turn from looking at fractions of a set (or group) to looking at representations of fractions of an area in two different contexts. You will notice a connection between these area contexts to the area work you did during the 2-D Geometry session. In this next activity you will work with hands-on materials to generate combinations of fractions and write addition equations that describe your combinations.

Pattern Block Cookies

Pattern Block Cookies is an area context used in grade three. Students bring their prior knowledge about pattern blocks from their work on 2-D Geometry in previous grade levels. In grades K-2 many students noticed the proportional relationships among pattern blocks; for example, they discovered that three triangles cover one trapezoid and they reasoned that if four trapezoids cover a given region then it would take 12 triangles to cover the same region. In grade three students now name the pattern blocks with fractional amounts.

In this activity you will explore pattern blocks using a virtual manipulative.

The hexagon represents one whole cookie. Look at each of the following pattern blocks and consider the part of the whole that each one represents:

  1. trapezoid (red) –two trapezoids fill the whole hexagon, so each one is 1/2.
  2. rhombus (blue) – three rhombi fill the whole hexagon, so each one is 1/3.
  3. triangle (green) – six triangles fill the whole hexagon, so each one is 1/6.

(Note that the squares and tan rhombuses are not used in this activity.)

Using the trapezoid, rhombus and triangle, find as many combinations as you can to make the whole – the hexagon.

Record the equations that describe your combinations on this handout. Also record other “fraction facts” that you discover including equivalencies for 1/2 and 2/3.

Here are additional possible equations.

*As a challenge, look for ways to make 5/6 without using any sixths.

As you were completing this activity, you kept lists of “Fraction Facts.” These “facts” were based on the visual model you were working with, not a procedure for finding equivalent fractions or for adding fractions. Which facts became apparent to you? Were there any combinations that were surprising to you?

4 x 6 Rectangles

In this activity, consider a 4 x 6 rectangle as 1 whole. This area model is similar to the geoboards you used during the 2-D Geometry session when you found different ways to show half of the 4 x 4 region.

*NOTE: 4 x 6 Rectangles are one of the grid sizes used in grade 4 to explore the area model of fractions. (Students also use 5 x 12 and 10 x 10 grids).

To begin, print out Fraction of an Area—4 x 6 Rectangles. Then shade the given fractional amounts (1/4, 2/3, and 5/8).

How do you know that these shaded amounts are exactly 1/4, 2/3, and 5/8 of the whole rectangle? How would you name the amount left unshaded?

When you worked with the pattern blocks you found some other ways to make one whole, such as 1/2 + 1/3 + 1/6 = 1. Does this equation still hold true for parts of the 4 x 6 rectangle?

Combinations that Equal 1

Print out Combinations That Equal 1. Represent the equation.

Shade 1/2 + 1/3 + 1/6 = 1 on one of the rectangles to see if it holds true.

Then find other combinations of fractions that equal 1 using the other rectangles on the page. When you have finished, click here to see some examples.

When you worked with the pattern blocks, you explored the relationships among a specific set of fractions: halves, thirds, and sixths. You used the blocks as a visual model to show equivalencies such as 2/6 = 1/3, combinations that equal one such as 1/2 + 1/3 + 1/6, and other relationships among halves, thirds, and sixths.

When you worked with the 4 x 6 rectangles you divided the whole area into a variety of parts: halves, thirds, and sixths as well as fourths, eighths, and twelfths.

These representations are important models to help us make sense of fractions. The work that students do in Investigations focuses on using multiple representations to develop mental images of fraction relationships.

Halves of Different Wholes

Each of these representations shows one-half, but each shows half of a different whole. Think about what is the same and what is different in these examples.

Write down your own observations, and then click the Show link to see what others might say.

  • ½ is always ½–one out of two equal parts.
  • However, the quantity represented by ½ depends on the size of the whole.
  • Coordinating these two ideas about fractions and what they represent is complex. It is part of the work that Investigations students do as they use a variety of area models, including rectangular grids with various dimensions.

Combining Fractions

To conclude this activity, you will apply the models and relationships you have just been working with to solve a problem about combining fractions.

Review the following problem. (The problem is from the Grade 3 unit Finding Fair Shares.)

Each bag holds 24 apples. Kim collected 1/3 of a bag. Phillip collected 2/4 of a bag. If they put all their apples together, would Kim and Phillip have 1 whole bag?

Even though this is a fraction of a set (of apples) problem, you may want to make use of the area representations to solve it.

Click the Show link to see how other teachers might solve this problem.

  • I know that 2/4 or 1/2 of the 4 x 6 rectangle would be 12 out of the 24 squares and 1/3 would be 8 squares (since 8 x 3 = 24). So 2/4 + 1/3 would be 12 + 8 squares or 20 out of 24 squares, so it isn't enough.
  • I know 2/4 = 1/2 from the rectangles. And I know 1/2 + 1/3 + 1/6 =1 from the pattern blocks. This is only 1/2 + 1/3, so it isn’t enough to fill a whole bag.
  • I know 2/4 + 1/2 = 1. Since 1/3 is less than 1/2, 2/4 + 1/3 will be less than 1.

Comparing Fractions

Overview

Up to now, the work you’ve been doing in this session has focused on understanding the meaning of fractions as parts of a whole and using visual models to understand fraction relationships. In this activity you’ll focus on thinking about the quantity represented by a fraction as we work on comparing fractions.

Ordering Fractions with Respect to Landmarks

Take a look at the Fractions in Containers diagram below.

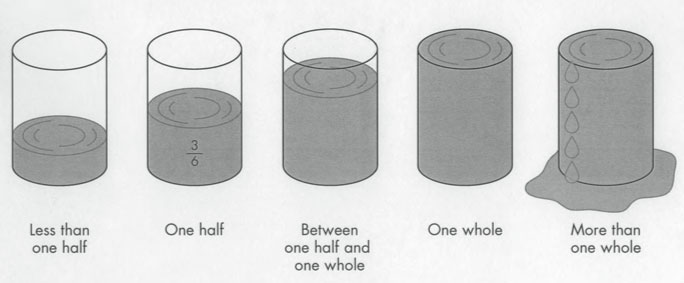
6 containers with sequential amounts

To begin thinking of fractions as quantities, we’ll begin by comparing them to some landmark numbers that we are familiar with: 0, 1/2, and 1. These containers provide us with a visual image of those landmarks.

One fraction has already been put into a container: 3/6 is in the one half container. Why does it belong there? What is another fraction that we could put into the one half container? How do you know it belongs there?

Next print out the Fractions in Containers worksheet and place some of the fractions listed into the containers.

What is true about all of the fractions in the [less than one half] container? What did you think about as you placed those fractions in the container?

Comparing Pairs of Fractions

Which fraction is greater, 3/7 or 1/2?

What strategies did you use to decide? Click the Show link to see strategies other teachers may have used.

  • Three and a half sevenths make a half so 3/7 is less.
  • 3/6 is a half, but sevenths are smaller than sixths. So 3/7 is less than 3/6.
  • If you had 7 cookies on a plate and you took 3, you'd leave 4. You would have taken fewer than half.
  • 3/7 is less than half because if you double it, it is only 6/7, which is less than a whole.
  • Change both fractions to fourteenths. 3/7 is 6/14, 1/2 is 7/14, so 1/2 is greater.

Some strategies incorporate fractions of a set (cookies) , some involve numerical reasoning (3/7 doubled is 6/7), some draw on area representations (sevenths are smaller than sixths.)

Now take a look at the page Fraction Pairs to Compare. Compare the pairs of fractions and decide which is larger. Find at least two ways to explain how you know which is the larger fraction in each pair.

Click the show link for a summary of the strategies one might use to solve these problems.

  • common numerator: 5/6 is larger than 5/8 because 1/6 is larger than 1/8 and they both have five pieces.
  • common denominator: 3/5 is 24/40, 5/8 is 25/40, so 5/8 is 1/40 larger than 3/5.
  • comparing one fraction to an equivalent of the other: 1/3 is equal to 2/6; 2/5 is larger than 2/6 because 1/5 is larger than 1/6; so 2/5 is more than 1/3.
  • closer to or further from one: 5/6 is only 1/6 away from 1, 3/4 is 1/4 away, so 3/4 has more missing so it is smaller.
  • closer to or further from one-half: 5/8 is 1/8 more than 1/2, 3/5 is only 1/10 more than 1/2.

Discussion

How are fractions the same and different from whole numbers? How did working with different models for fractions affect your own understanding and how will it impact your teaching?

Go to the Forum

Key Learning

  • Fractions as relationship between two numbers, as a quantity, as parts of an area.
  • The role of the whole when comparing fractions.
  • Using landmarks to compare fractions.

This session is aligned with the following K-2 Units in Investigations.