Overview

Session Summary

This session is an introduction to algebraic reasoning in the context of number and operations. You will explore making generalizations related to addition and subtraction, and identify generalizations in the work of students. You will also consider the role of the teacher in eliciting algebraic reasoning.

Algebra is frequently described as “generalized arithmetic.” When students recognize patterns and relationships and make rules about them, they are beginning to work with algebraic ideas.

Part of the work in the elementary grades is helping students verbalize rules or generalizations for the patterns and relationships they see in their work with numbers and operations, and consider such questions as:

• Is this always true?
• Does it work for all numbers?
• How can we know?

These ideas give students powerful tools for working with numbers and operations.

Mathematics in this session

• Create equivalent expressions for a number
• Identify and examine generalizations about numbers and operations
• Consider the teacher’s role in connecting computation work to algebraic reasoning

Common Core Alignment

The content in this session is aligned to the following Common Core State Standards and Math Practices:

MATH STANDARDS

Understand addition as putting together and adding to, and understand subtraction as taking apart and taking from.

K.OA.1. Represent addition and subtraction with objects, fingers, mental images, drawings¹, sounds (e.g., claps), acting out situations, verbal explanations, expressions, or equations.

K.OA.3. Decompose numbers less than or equal to 10 into pairs in more than one way, e.g., by using objects or drawings, and record each decomposition by a drawing or equation (e.g., 5 = 2 + 3 and 5 = 4 + 1).

K.OA.4. For any number from 1 to 9, find the number that makes 10 when added to the given number, e.g., by using objects or drawings, and record the answer with a drawing or equation.

Represent and solve problems involving addition and subtraction.

1.OA.1. Use addition and subtraction within 20 to solve word problems involving situations of adding to, taking from, putting together, taking apart, and comparing, with unknowns in all positions, e.g., by using objects, drawings, and equations with a symbol for the unknown number to represent the problem.¹

1.OA.2. Solve word problems that call for addition of three whole numbers whose sum is less than or equal to 20, e.g., by using objects, drawings, and equations with a symbol for the unknown number to represent the problem.

Understand and apply properties of operations and the relationship between addition and subtraction.

1.OA.3. Apply properties of operations as strategies to add and subtract.2 Examples: If 8 + 3 = 11 is known, then 3 + 8 = 11 is also known. (Commutative property of addition.) To add 2 + 6 + 4, the second two numbers can be added to make a ten, so 2 + 6 + 4 = 2 + 10 = 12. (Associative property of addition.)

1.OA.4.Understand subtraction as an unknown-addend problem. For example, subtract 10 – 8 by finding the number that makes 10 when added to 8. Add and subtract within 20.

1.OA.6. Add and subtract within 20, demonstrating fluency for addition and subtraction within 10. Use strategies such as counting on; making ten (e.g., 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); decomposing a number leading to a ten (e.g., 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9); using the relationship between addition and subtraction (e.g., knowing that 8 + 4 = 12, one knows 12 – 8 = 4); and creating equivalent but easier or known sums (e.g., adding 6 + 7 by creating the known equivalent 6 + 6 + 1 = 12 + 1 = 13).

Work with addition and subtraction equations.

1.OA.7. Understand the meaning of the equal sign, and determine if equations involving addition and subtraction are true or false. For example, which of the following equations are true and which are false? 6 = 6, 7 = 8 – 1, 5 + 2 = 2 + 5, 4 + 1 = 5 + 2.

1.OA.8. Determine the unknown whole number in an addition or subtraction equation relating three whole numbers. For example, determine the unknown number that makes the equation true in each of the equations 8 + ? = 11, 5 = _ – 3, 6 + 6 = _.

Represent and solve problems involving addition and subtraction.

2.OA.1. Use addition and subtraction within 100 to solve one- and two-step word problems involving situations of adding to, taking from, putting together, taking apart, and comparing, with unknowns in all positions, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem.¹

Add and subtract within 20.

2.OA.2. Fluently add and subtract within 20 using mental strategies.2 By end of Grade 2, know from memory all sums of two one-digit numbers.

Work with equal groups of objects to gain foundations for multiplication.

2.OA.3. Determine whether a group of objects (up to 20) has an odd or even number of members, e.g., by pairing objects or counting them by 2s; write an equation to express an even number as a sum of two equal addends.

Use place value understanding and properties of operations to add and subtract.

2.NBT.5. Fluently add and subtract within 100 using strategies based on place value, properties of operations, and/or the relationship between addition and subtraction.

2.NBT.7. Add and subtract within 1000, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method. Understand that in adding or subtracting three-digit numbers, one adds or subtracts hundreds and hundreds, tens and tens, ones and ones; and sometimes it is necessary to compose or decompose tens or hundreds.

2.NBT.9. Explain why addition and subtraction strategies work, using place value and the properties of operations.¹

¹Explanations may be supported by drawings or objects.

Solve problems involving the four operations, and identify and explain patterns in arithmetic.

3.OA.8. Solve two-step word problems using the four operations. Represent these problems using equations with a letter standing for the unknown quantity. Assess the reasonableness of answers using mental computation and estimation strategies including rounding.³

3.OA.9. Identify arithmetic patterns (including patterns in the addition table or multiplication table), and explain them using properties of operations. For example, observe that 4 times a number is always even, and explain why 4 times a number can be decomposed into two equal addends.

³ This standard is limited to problems posed with whole numbers and having whole-number answers; students should know how to perform operations in the conventional order when there are no parentheses to specify a particular order.

Use place value understanding and properties of operations to perform multi-digit arithmetic.¹

3.NBT.1. Use place value understanding to round whole numbers to the nearest 10 or 100.

3.NBT.2. Fluently add and subtract within 1000 using strategies and algorithms based on place value, properties of operations, and/or the relationship between addition and subtraction.

3.NBT.3. Multiply one-digit whole numbers by multiples of 10 in the range 10–90 (e.g., 9 × 80, 5 × 60) using strategies based on place value and properties of operations. 1 A range of algorithms may be used.

Generate and analyze patterns.

4.OA.5. Generate a number or shape pattern that follows a given rule. Identify apparent features of the pattern that were not explicit in the rule itself. For example, given the rule “Add 3” and the starting number 1, generate terms in the resulting sequence and observe that the terms appear to alternate between odd and even numbers. Explain informally why the numbers will continue to alternate in this way. Write and interpret numerical expressions.

5.OA.1. Use parentheses, brackets, or braces in numerical expressions, and evaluate expressions with these symbols.

MATH PRACTICES

Note: All are illustrated in this session, though not all at once.

MP1: Make sense of problems and persevere in solving them

MP2: Reason abstractly and quantitatively

MP3: Construct viable arguments and critique the reasoning of others

MP4: Model with mathematics

MP5: Use appropriate tools strategically

MP6: Attend to precision

MP7: Look for and make use of structure

MP8: Look for and express regularity in repeated reasoning

You may also wish to review the full set of Common Core State Standards in Math and/or videos of the Math Practices enacted in Investigations.

Readings

Making Equivalent Problems

This session is about algebraic reasoning. Think about what comes to mind when you think about algebra.

Many adults think of algebra in terms of x’s and y’s, manipulating symbols, and solving equations.

Algebra includes work with patterns, functions, and changes. Our focus in this session will be limited to patterns and generalizations about addition and subtraction problems.

Looking at Leah’s Work

The following is an example of a student reasoning algebraically. Leah is a first grader using what she knows about how numbers work.

Within the context of specific numbers, Leah is using the idea that if you take 1 away from one of the addends, the answer will decrease by 1. Part of the work we will be doing in this session is examining the generalizations that underlie the strategies students use to solve addition and subtraction problems.

Addition Equivalent Problems: Today’s Number

Today’s Number is a routine introduced in second grade to provide regular practice with number combinations and to develop flexibility with number. Students write equations for the number of days they have been in school, the day of the month, or some other number selected by the teacher.

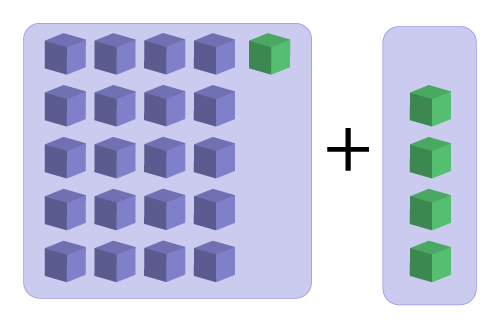
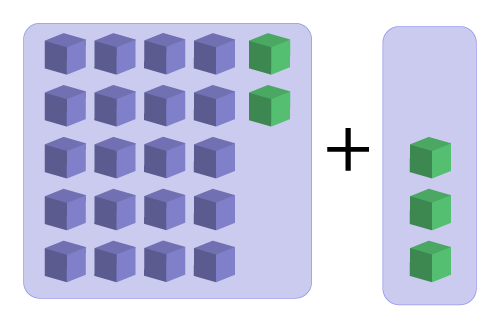
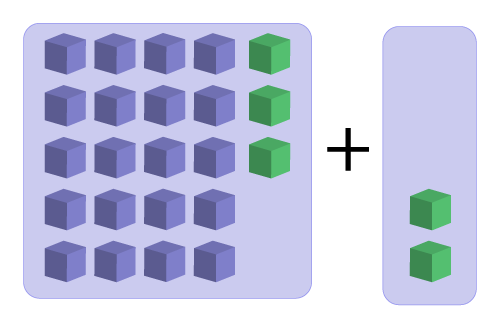
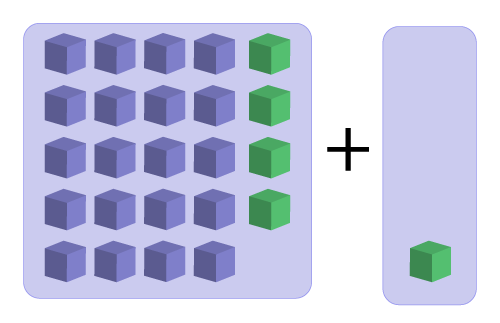
For the purpose of this activity, today’s number is 25. Here are a series of equations using addition to get 25.

Write a statement about the relationship between the two addends in this series of equations.

Does your statement apply to this series of problems as well? If not, come up with a rule that applies to both problems. When you have finished, click the show link to see what other possible rules there might be.

Here's an example:

Changing the Addends

Use your rule to help you solve this problem: 57 + 38

Change the addends to make the problem easier to solve. Click the show link to see a few possible solutions.

Subtraction Equivalent Problems

Here are a few equations using subtraction to equal 25:

Write a rule about what happens when you change one of the numbers in a subtraction equation. Test your rule using examples. Click the show link to see examples of possible rules.

Use an equivalent method to solve one or both of the following problems:

There are many activities in Investigations where students work on making equivalent problems. This idea begins in Kindergarten. Here is a sample of the activities where the idea can be highlighted.

NOTE: the activities do not teach this idea. The activities provide a context for exploring equivalent problems, and your questions are what lead to that exploration and lead the students to think about how the numbers behave.

Generalizing Arithmetic

Overview

Part of the work in the elementary grades is helping students verbalize rules or generalizations for the relationships they see, and consider such questions as: Is this always true? Does it work for all numbers? How can we know? The teacher in this video clip pushes her students to prove that their generalization about the order of numbers in addition will always work.

Follow along with the transcript if you would like. As you view the video, keep the following questions in mind. Click the show link after you have considered the question yourself.

1. What is the math that students are working on? What do they understand about addition?

2. What generalizations are students making? How are they describing and justifying their generalizations?

3. How does their cube model relate to the specific example of 23 + 2? How does the modeling go beyond the specific example?

4. What is the teacher’s role in this discussion?

Teachers’ questions are critical to moving students to think algebraically. The following list includes some possible Questions that Promote Algebraic Thinking.

Looking at Student Work

Overview

You have made some generalizations about how addition and subtraction work and have seen students using and justifying their generalizations. Now we will delve more deeply into student thinking. As you consider the set of student work below, go beyond describing the strategy the student used to solve the problem, to identifying the underlying generalization the student is using. Refer to the Looking at Student Work questions and use them as a guide as you look at the student work samples. Start by looking at Yoshi’s work.

Using the annotation tool, examine 2 or 3 additional pieces of student work and decide what generalization(s) each student is using in the solution strategy. Share your thoughts by responding to the prompt below each student work sample. Be sure to click Submit Responses when you are done.

Look at the Addition and Subtraction Generalizations and see if you found evidence of any of them in the student work.

At each grade level there are resources in each unit in the number and operations strand (except in the fractions units) that can help you learn more about specific algebraic ideas that are connected to the computation work students are doing. Each unit in the number and operations strand (except the fractions units) has an algebra essay. You can read about the algebra ideas in the unit and there are algebra sidebars throughout the number units that highlight connections to algebraic ideas. Deborah Schifter’s words below speak to the importance of and connection between building on children’s mathematical ideas and seeing them think algebraically:

"When instruction is designed to build on children’s mathematical ideas and to foster children’s mathematical curiosity, children are likely to exhibit algebraic ways of thinking in the context of lessons in arithmetic, geometry, or measurement." D. Schifter, personal communication, 2006

It is the role of the teacher to challenge students to take everyday assignments and think about relationships, make rules or generalizations, and ‘prove’ that their rules will always work.

If children’s algebraic ideas are highlighted and valued from an early age, they will enjoy exploring algebra.

Discussion

1. How will the work on algebraic reasoning help students with their fluency with computation?
2. In what ways will you capitalize on the work you are already doing in number to highlight algebraic reasoning ideas?
3. How will what you learned in this course affect your teaching?

Go to the Forum

Key Learning

• Students naturally make generalizations about the ways that numbers and operations behave. The teacher's role is to make those explicit and useful.
• Questions the teacher poses, such as "Is this always true? Does it work for all numbers? How can we know?" help students verbalize generalizations. The ideas give students powerful tools for working with numbers and operations.